Для тестирования предлагаются 10 вариантов. Варианты 1-5 соответствуют первому уровню, в который входят, как правило, вопросы обязательного уровня обучения; варианты 6-10 - второму уровню, который требует более глубокого знания изучаемого материала. Для каждого варианта определен входящий номер задания:
Их трех предложенных ответов нужно выбрать один, правильный на взгляд ученика – он же является и номером следующего задания, который нужно решить. Таким образом, для решения одного варианта нужно последовательно решить пять задач. На выходе варианта учащийся получает трехзначный цифровой шифр, который в соответствии с таблицей шифров :
«2» - если он допустил три и более ошибок.
Учителю практически не требуется время на проверку – достаточно посмотреть на конечный шифр и определить оценку по таблице шифров.
для соответствующих заданий, учитель может предложить учащимся работать в режиме самоконтроля, при котором учащийся самостоятельно переходит к более сложным заданиям; в том случае, если учащегося не устраивает конечный результат, он, как правило, самостоятельно стремится еще раз «пройти» по цепочке заданий.
| №п/п | Задание | Код перехода |
| 1(2) | Найти область определения функции x≠ , k є Z x ≠ πk, k є Z x≠ ± + , k є Z |
…44 …43 …45 |
| 2(2) | Определить, при каких значениях х функция у = существует? X ≠ + , k є Z X ≠ , k є Z X ≠ + , k є Z
|
…45 …49 …13 |
| 3 (2) | Определить, при каких значениях х функция у =tgx существует X ≠ + πk , k є Z X ≠ , k є Z X ≠ + , k є Z |
…13
…49 …45 |
| 4(2) | Найти область определения функции y = X ≠ + , k є Z X ≠ + , k є Z X ≠ + , k є Z |
…7
…20
…49 |
| 5 (2) | Найти нули функции у = 2sin 3x 1) ± + , k є Z 2) , k є Z 3) (-1)k + πk , k є Z |
…7 …49
…20 |
| 6(2) | Записать значения sin(-200),sin 900, sin 200 в порядке возрастания sin 200 , sin(-200), sin 900 sin(-200), sin 900, sin 200 sin(-200), sin 200 , sin 900 |
…44 …36 …37 |
| 7 (2) | Записать значения cos, cos(- -), cos в порядке убывания cos , cos(- -), cos cos(- -), cos, cos cos , cos, cos(- -) |
…42
…22 …32 |
| 8 (2) | Записать значения tg( -400), tg600, tg 1000 в порядке возрастания tg( -400), tg600, tg 1000 tg600 , tg( -400), tg 1000 tg 1000 , tg600 , tg( -400), |
…3 …2 …1 |
| 9 (1) | Найти область значения функцииsin 2x ( -∞; + ∞) [ -1 ; 1] [ -2; 2 ] |
…4 …30 …5 |
| 10(1) | Найти область определения функцииsin 2x ( 0; 2π) [ + 2πк; + 2πк], k є Z ( -∞; + ∞) |
…5 …4 …2 |
| 11(1) | На каком рисунке изображен график функции у = sin x ? 1) 2) 2)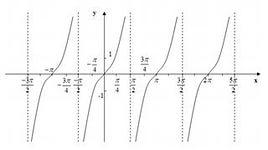 3) 3) 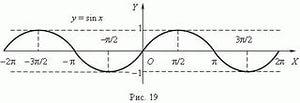 |
1)…10 2) …12 3) …8
|
| 12(1) | Найдите допустимые значения х для функции y = tg x Любое число, кроме х + πk , k є Z [ + πк; + πк], k є Z Любое действительное число |
…2 …4
…5 |
| 13(2) | Вычислить значение функции у = cos 2x, если sin x = и 3/5 – 3/5 – 7/25 |
…32 …22 …17 |
| 14(2) | Какая из функций является ни четной, ни нечетной У = Y = Y = x cosx |
…103
…108 …106 |
| 15(3) | Найти промежутки убывания функции у = sin ( 3x - ) 1)[ + 2πк; + 2πк] , k є Z 2)[ + ; +] k є Z
3)[ + ; + ] k є Z |
…114
…115
…104 |
| 16(3) | Какая из функций является четной? У = х sin2x У = x2cosx У = |
…30 …29 …47 |
| 17(2) | Вычислите значение функции у = cos2x, если cos х = 12/13 и х находится в первой четверти 119/169 5/13 25/169 |
…103 …101 …102 |
| 18(1) | Найти область значения функцииcos 3х ( -∞; + ∞) [ -3; 3] [ -1 ; 1] |
…5 …4 …30 |
| 19(2) | Какая из функций является нечетной? Y = x2tgx( cos2x +1) Y = x3tgx Y = x + sin2x |
…37 …36 …46 |
| 20(2) | Найдите наименьшее значении функции у = 1 – 4sinx – 3 0 - 4 |
…42 …22 …32 |
| 21(2) | На каком рисунке изображен график функции y = cos x? 1)  2) 2)  3) 3) 
|
1) …25 2) …10 3) …9 |
| 22(1) | Каков наименьший период функции y = cos x? π 2π π/2 |
…102 …105 …101 |
| 23(2) | Найдите наименьшее значении функции у = 2 +tg2x 2 1 Не существует |
…102 …101 …106 |
| 24 (2) | Найдите наибольшее значении функции y = 2 – 3cosx 2 5 -1 |
…103 …108 …106 |
| 25 (2) | Найдите наименьшее значении функции у = 2 tgx – 3 Не существует – 1 -5 |
…6 …30 …3 |
| 26 (1) | Найти область значения функции у = 2 tgx [ -2; 2 ] ( 0: 1) Любое действительное число |
…5 …4 …28 |
| 27 (2) | Решите уравнение sin ( + ) = 1 + 2πк; k є Z 4πk ;k є Z 2πк; k є Z |
…17 …41 …23 |
| 28 (2) | Решите уравнение tg ( 2x + ) = , k є Z + πk , k є Z + πk , k є Z |
…46 …13 …49 |
| 29 (2) | Решите уравнение sin ( - ) = 0 1)πk , k є Z 2)π + 2πk, k є Z 3) + 2πk , k є Z |
…44 …43 …36 |
| 30 (2) | Решите уравнение 2 cos ( -2x) = 1 (-1)k + πk , k є Z +2πk , k є Z
± + πk , k є Z |
…13 …49
…36 |
| 31 (2) | На каком рисунке изображен график функции y = tgx? 1)  2) 2)  3) 3) 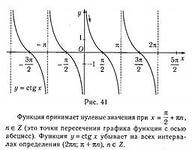 | 1)…16 2)…9 3)…18 |
| 32 (1) | Каков наименьший положительный период функции у = sinx π/2 π 2π |
…102 …101 …105 |
| 33 (1) | Вычислить arcsin ½ π/6 5π/6 π/3 |
…34 …18 …26 |
| 34 (2) | Решите уравнение cos ( - ) = 1 2πk , k є Z 2) +πk , k є Z 3) + 4πк, k є Z |
…30 …28
…19 |
| 35 (3) | Найти промежутки убывания функции у = cos ( 2x + ) [πк ; π/2 + πк] , k є Z [ -π/4 + πк; π/4 + πк], k є Z [π/4 + πк ; 3π/4 + πк ], k є Z |
…114 …124 …107 |
| 36 (2) | Решите уравнение tg ( 2x – π/3) = 0 +πk , k є Z 2) + , k є Z 3) ± + , k є Z |
…23 …14
…17 |
| 37 (2) | Найти корни уравнения cos ( 3x - ) = 1 +, k є Z +2πk, k є Z + πk, k є Z |
…35
…14 …24 |
| 38 (2) | Найти корни уравнения tg ( + ) = 1 2πk, k є Z + πk, k є Z , k є Z |
…40 …50
…28 |
| 39 (1) | Вычислить arcos π/3 π/6 –π/6 |
…48 …38 …18 |
| 40(2) | Через какую точку проходит график функции y = 2cosx? (π; 2) (π/2; 1) (0;1) |
…46 …27 …37 |
| 41 (2) | Через какую точку проходит график функции y = sin2x? ( 0;0 ) (0; π) (π/2; 1) |
…107 …110 …111 |
| 42 (1) | Найти наименьший положительный период функции y = tgx 2π π Не существует |
…102 …105 …101 |
| 43 (2) | Найти наименьший положительный период функции y = sin 2,5x + 1 2π 3π/2 4π/5 |
…14 …24 …15 |
| 44 (2) | Найти наименьший положительный период функции y = 2 – cos 1,5x 3π/2 4π/3 2π |
…17 …14 …23 |
| 45 (2) | Найти наименьший положительный период функции y = 2tg 3π/2 π 2π/3 |
…14 …17 …23 |
| 46 (2) | Найти минимумы функции y = sinx – 1 -1 -3/2 -1/2 |
…17 …41 …23 |
| 47 (2) | Найти корни уравнения tg ( 4x – π/3) = , k є Z + , k єZ + πk, k є Z |
…13
…45 …49 |
| 48 (1) | Каким свойством обладает функция y = 2sinx? Четная Возрастающая при всех х нечетная |
…4 …5 …50 |
| 49 (2) | Найти корни уравнения tg ( 5x –π/8) = 0 + , k єZ + πk, k є Z + 5πk, k є Z |
… 17 …22
…32 |
| 50 (2) | Найти корни уравнения sin (3х + ) = 0 +2 πk, k є Z , k єZ k є Z |
…13 …27
…49 |
| 51 (2) | Найдите sinα, если cos α = -3/5 и π/2 α π – 4/5 4/5 1/2 |
…94 …93 …95 |
| 52 (2) | Упростить выражение Sin α 2tg α 2cos α |
…99 …95 …93
|
| 53 (2) | Упростить выражение ( 1- tg2α) cos2α Sin2α Sin2α Cos2α |
…99 …63 …95 |
| 54 (2) | При каких значениях х функция у = cos равнa нулю? π + 2πк , к є Z + πk, k є Z +2 πk, k є Z |
…99
…57 …70 |
| 55 (2) | При каких значениях х функция у = sinx∙ cosx равнa нулю? , k єZ πk, k є Z + πk, k є Z |
…99
…57 …70 |
| 56 (2) | Найти корни уравнения 2sin 3x -1 =0 (-1)k + , k єZ (-1)k + πk , k є Z ± +2 πk , k є Z |
…87 …86
…94 |
| 57 (2) | При каких значениях х выражение cos(2x - ) равно 1? + 4πk, k є Z + πk , k є Z + 2πk , k є Z |
…72
…92 …82 |
| 58 (2) | Решите неравенство sin x ( - + 2πk , + 2πk), k є Z ( + 2πk, + 2πk) , k є Z ( - + 2πk, + 2πk), k є Z |
…52
…51
…53 |
| 59 (2) | Решите неравенство cos x ≤ - [ + 2πk , + 2πk], k є Z [- + 2πk , + 2πk], k є Z [- + 2πk ,- + 2πk], k є Z |
…80
…55 …54 |
| 60 (2) | Решите неравенство tg x ≤ [ πn; + πn], n є Z [ + πn; + πn] . n є Z [ - + πn; + πn ], n є Z |
…55 …54
…52 |
| 61 (1) | Решите уравнение 2 cos x = 1) ± + 2πk, k є Z 2) (-1)k +2πk, k є Z 3) + 2πk, k є Z |
… 58 … 62 …60 |
| 62 (2) | Найдите cos α , если sinα = 3/5 и π/2 α π 1) -4/5 2) 4/5 3) 1/2 |
… 52 … 55 … 54 |
| 63 (2) | Найдите sinα, если cos α = 3/5 и 0 1) -4/5 2) 4/5 3) 1/2 |
… 82 … 67 … 72 |
| 64 (3) | Упростить выражение 1) 2 tgα 2) 2сtgα 3) sinα |
… 117 … 120 … 113 |
| 65 (3) | Решите неравенство 2sin (3x - )≥ 1) [ + +], k є Z 2) [ + ;π + ], k є Z 3) [ - + +], k є Z |
…116
…119 …117 |
| 66 (2) | Упростить выражение 1) sin 2) 2 3) 2сtg |
…97 …80 …79 |
| 67 (2) | Упростить выражение cos2 α - cos 4α+ sin4 α 1) cos2 α 2) sin2 α 3) cos 4α |
…112 …121 …118 |
| 68 (2) | Решите уравнение sin( - ) = 0 1) 2πk, k є Z 2) πk, k є Z 3) ± + πk, k є Z |
…80 ….55 …54 |
| 69 (3) | Найти область определения функции у = 1)[- + πn; + πn] , n є Z 2) [ + πn; + πn] , n є Z 3) )[- + πn; + πn] , n є Z |
…87 … 86
… 96 |
| 70 (2) | Решите уравнение cos( -3 x) =1 1) , k є Z 2) πk, k є Z 3) + 2πк, k є Z |
…92 …82 …72 |
| 71(1) | Решите уравнение sinх – 1) (-1)k +πk, k є Z 2) (-1)k +2πk, k є Z 3) ± + 2πk, k є Z |
…75
…60 …59 |
| 72 (1) | Решите уравнение 2 sinх = 1 1) ± + 2πk, k є Z 2) (-1)k +πk, k є Z 3) (-1)k +2πk, k є Z |
…109 …112
…118 |
| 73(2) | Решите уравнение tg(2х - ) =0 1) πk, k є Z 2) +πk, k є Z 3) + к, k є Z |
…112 …109
…122 |
| 74(3) | Решите уравнение 2 sin2 х -3 sin х = -1 1) (-1)k +πk, k є Z 2) +2πk; (-1)k +πk, k є Z 3) ± + 2πk; +2πk, k є Z |
…120 …119
…113 |
| 75 (2) | При каких значениях х выражение sin (2х -) равно нулю? 1) πk, k є Z 2) + к, k є Z 3) +2πk, k є Z |
…80 …56
…53 |
| 76 (2) | Решите неравенство sinх ≤ - 1) [ + 2πn; + 2πn] , n є Z 2) [- + 2πn; +2πn] , n є Z 3) [- + 2πn; +2πn] , n є Z |
…78
…55 …54 |
| 77 (3) | Найдите промежутки убывания функции у = cos( - ) 1) ( + 4πn; + 4πn), n є Z 2) ( + 4πn; + 4πn), n є Z 3) ( + 4πn; + 4πn), n є Z |
…67
…91 …73 |
| 78 (2) | Решите неравенство cos x ˃ 1) ( + 2πn; + 2πn), n є Z 2) ( + 2πn; + 2πn), n є Z 3) ( + 2πn; + 2πn), n є Z |
…99
…96 …63 |
| 79 (3) | Найти область определения функции у = 1) ( + 2πn; + 2πn), n є Z 2), n є Z 3) [- + 2πn; 2π(n+1)] , n є Z |
…94 …93 …86 |
| 80 (2) | Решить неравенство tg x ≥ - 1) ( + πn; + πn), n є Z 2) [ + πn; + πn] , n є Z 3)( + πn; + πn] , n є Z |
…63
…86 …99
|
| 81(1) | Решите уравнение cox -1 = 0 1) 2πk, k є Z 2) ± + πk, k є Z 3) πk, k є Z |
…66 …68 …59 |
| 82 (1) | Решите уравнение sin x – 1 = 0 1) + πk, k є Z 2) πk, k є Z 3) + 2πk, k є Z |
…118 …109 …112 |
| 83(1) | Решите уравнение 3 tg x = 1) + πk, k є Z 2) + πk, k є Z 3) ± + πk, k є Z |
…68 …84 …76 |
| 84(2) | Найдите cos α , если sinα = и угол α принадлежит II четверти 1)- 2) 3) |
…78 …80
…69 |
| 85(3) | Решить неравенство 2cos ( - ) 1) ( + 2πn; + 2πn), n є Z 2)( 4πn; + 4πn), n є Z 3)(- + 4πn; 4πn), n є Z |
…119
…123 …117 |
| 86(3) | Найдите промежутки убывания функции у = sin ( -4х) 1) + +), k є Z 2)+ +), k є Z 3)( +), k є Z |
…64 …67
…73 |
| 87(3) | Решите уравнение sin2x + sin 2x – 3 cos2x =0 1) + πn; + 2πn, n є Z 2) ± + πn, arctg (-3) + πn, n є Z 3) + πn, arctg (-3) + πn, n є Z |
…74 …64
…85 |
| 88(2) | Найдите cos α , если sinα = и угол α принадлежит I четверти 1)- 2) 3) |
…78 …90
…100 |
| 89(1) | Решите уравнение cox – 0,5 =0 1) (-1)k +πk, k є Z 2) ± + πk, k є Z 3) ± +2 πk, k є Z |
…98 …68
…88 |
| 90(3) | Упростите выражение 4sin 1) 2) sin4 3) sin2 |
…96 …87 …77 |
| 91(3) | Решите уравнение 2tg x – 3 ctg x -1 = 0 1)arctg 1,5+ πk; + πk, к є Z 2) ± + πk, k є Z 3) arctg 1,5+ πk; + πk, к є Z |
…119 …113
…120 |
| 92(1) | Решите уравнение tg x – 1 = 0 1) ± + πk, k є Z 2) + πk, k є Z 3) + 2πk, k є Z |
…109 …112
…118 |
| 93(3) | Решите уравнение sin x + cos x = 1 1) + 2πk; 2πk, k є Z 2)к, k є Z 3) ± +2πk, k є Z |
…65 …64
…74 |
| 94(3) | Найдите промежутки возрастания функции у = cos ( 3х +) 1) ( + , k є Z 2) ( + , k є Z 3) ( + , k є Z |
…67 …64
…73 |
| 95(3) | Найдите промежутки возрастания функции у = sin( 2х +) 1)( + 2πk; π(k+1), k є Z 2) ( + πк; + πк), к є Z 3) ( + πк; + πк), к є Z |
…64 …73
…67 |
| 96(3) | Найдите промежутки возрастания функции у = sin( 4х -) 1) (- + , k є Z 2) ( + , k є Z 3) ( + , k є Z |
…67 ..91
…73 |
| 97(2) | Решите уравнение 2sin = 1 1) ± +2πk, k є Z 2) (-1)k +2πk, k є Z 3) (-1)k +πk, k є Z |
…99 …95
…83 |
| 98(2) | Найти корни уравнения cos ( 4х +) 1), k є Z 2), k є Z 3) +πk, k є Z |
…100 …54
…55 |
| 99(2) | При каком значении х выражение cos ( - ) равно 1? 1) ± +2πk, k є Z 2) +6πk, k є Z 3) 2πk, k є Z |
…72 …67
…82 |
| 100(2) | Решите неравенство sinх 1) ( + 2πк; + 2πк), к є Z 2) ( + 2πк; + 2πк), к є Z 3) ( + 2πк; + 2πк), к є Z |
…63 …99
…77 |







 2)
2) 3)
3) 
 3)
3) 










