Параллелепипед и призма. Вариант 1
№ 1. Площадь диагонального сечения куба равна 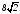 см2. Найдите площадь поверхности куба.
см2. Найдите площадь поверхности куба.
а) 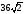 см2; б)
см2; б) 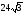 см2; в)
см2; в) 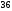 см2; г)
см2; г) 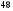 см2.
см2.
№ 2. Длины диагоналей трех граней прямоугольного параллелепипеда, имеющие общую вершину, равны  см,
см, 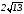 см и
см и 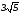 см. Найдите диагональ параллелепипеда.
см. Найдите диагональ параллелепипеда.
а) 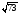 см; б)
см; б) 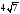 см; в)
см; в) 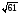 см; г)
см; г) 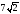 см.
см.
№ 3. Стороны основания прямого параллелепипеда равны 1 см и 3 см, а синус угла между ними равен 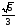 . Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно
. Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно 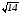 см.
см.
а) 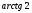 ; б)
; б) 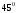 ; в)
; в) 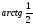 ; г)
; г) 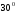 .
.
№ 4. Площади двух диагональных сечений прямого параллелепипеда равны 48 см2 и 30 см2, а боковое ребро равно 6 см. Найдите площадь основания параллелепипеда, если оно является ромбом.
а) 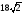 см2; б)
см2; б) 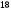 см2; в)
см2; в)  см2; г)
см2; г) 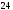 см2.
см2.
№ 5. Сторона основания правильной шестиугольной призмы равна 4 см, а большая диагональ призмы образует с основанием угол, равный 600. Найдите площадь полной поверхности призмы.
а) 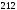 см2; б)
см2; б) 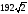 см2; в)
см2; в) 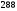 см2; г)
см2; г)  см2.
см2.
№ 6. АВСА1В1C1 – наклонная треугольная призма. Двугранный угол при ребре АА1 равен 900. Расстояния от ребра АА1 до ребер ВВ1 и СС1 равны соответственно 4 см и 3 см. Найдите площадь боковой поверхности призмы, если её высота равна  см и боковое ребро образует с основанием угол 600.
см и боковое ребро образует с основанием угол 600.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 7. АВСА1В1C1 – правильная треугольная призма. Через ребро А1В1 и точку М – середину АС - проведено сечение, площадь которого равна  см2. Найдите высоту призмы, если сторона её основания равна 2 см.
см2. Найдите высоту призмы, если сторона её основания равна 2 см.
а)  см; б)
см; б)  см; в)
см; в)  см; г)
см; г)  см.
см.
№ 8. АВСDА1В1C1D1 – прямоугольный параллелепипед. Причем АВ =  см, ВС =
см, ВС =  см, ВВ1 =
см, ВВ1 =  см. Через точки А, В1 и С проведена плоскость. Найдите тангенс угла между плоскостями АВ1С и АВС.
см. Через точки А, В1 и С проведена плоскость. Найдите тангенс угла между плоскостями АВ1С и АВС.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Параллелепипед и призма. Вариант 2
№ 1. Площадь поверхности куба равна  см2. Найдите площадь диагонального сечения этого куба.
см2. Найдите площадь диагонального сечения этого куба.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 2. Длины диагоналей трех граней прямоугольного параллелепипеда, имеющие общую вершину, равны  см,
см,  см и
см и  см. Найдите диагональ параллелепипеда.
см. Найдите диагональ параллелепипеда.
а)  см; б)
см; б)  см; в)
см; в)  см; г)
см; г)  см.
см.
№ 3. Стороны основания прямого параллелепипеда равны 2 см и 4 см, а синус угла между ними равен  . Найдите угол, который образует меньшая диагональ параллелепипеда с основанием, если её длина равна
. Найдите угол, который образует меньшая диагональ параллелепипеда с основанием, если её длина равна  см.
см.
а)  ; б)
; б) 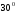 ; в)
; в)  ; г)
; г) 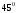 .
.
№ 4. Площади двух диагональных сечений прямого параллелепипеда равны 16 см2 и 27 см2. Основанием параллелепипеда является ромб, площадь которого равна 24 см2. Найдите длину бокового ребра параллелепипеда.
а)  см; б)
см; б)  см; в)
см; в)  см; г)
см; г)  см.
см.
№ 5. Сторона основания правильной шестиугольной призмы равна 6 см, а большая диагональ призмы образует с основанием угол, равный 300. Найдите площадь полной поверхности призмы.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 6. АВСА1В1C1 – наклонная треугольная призма. Двугранный угол при ребре ВВ1 равен 600, а расстояния от ребра ВВ1 до ребер АА1 и СС1 равны соответственно 1 см и 2 см. Найдите площадь боковой поверхности призмы, если её высота равна  см, а боковое ребро образует с основанием угол 300.
см, а боковое ребро образует с основанием угол 300.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 7. МКРМ1K1P1 – правильная треугольная призма, сторона основания которой 4 см. Найдите площадь сечения призмы плоскостью, проходящей через точки Р, Е и F, где Е и F – середины ребер М1Р1 и К1Р1, а боковое ребро равно 3 см.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 8. АВСDА1В1C1D1 – прямоугольный параллелепипед, причем ВС =  , СD =
, СD =  , СС1 =
, СС1 =  . Найдите тангенс угла между плоскостями ВС1D и АВС.
. Найдите тангенс угла между плоскостями ВС1D и АВС.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.





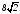 см2. Найдите площадь поверхности куба.
см2. Найдите площадь поверхности куба. 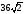 см2; б)
см2; б) 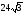 см2; в)
см2; в) 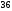 см2; г)
см2; г) 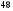 см2.
см2.  см,
см, 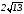 см и
см и 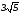 см. Найдите диагональ параллелепипеда.
см. Найдите диагональ параллелепипеда.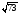 см; б)
см; б) 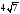 см; в)
см; в) 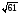 см; г)
см; г) 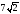 см.
см. 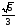 . Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно
. Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно 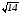 см.
см.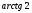 ; б)
; б) 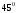 ; в)
; в) 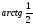 ; г)
; г) 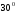 .
.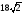 см2; б)
см2; б) 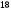 см2; в)
см2; в)  см2; г)
см2; г) 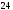 см2.
см2. 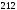 см2; б)
см2; б) 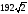 см2; в)
см2; в) 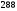 см2; г)
см2; г) 









