Просмотр содержимого документа
«Тест по теме "Четырехугольники"»
Тест 1 «Четырехугольники»
Вариант I.
1. Периметр параллелограмма ABCD равен 30 см, а его диагональ BD – 9 см. Найдите периметр ABD.

2. Периметр квадрата равен 24 см. Найдите его сторону.
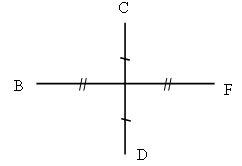
3. Отрезки BF и DC перпендикулярны и точкой пересечения делятся пополам. Тогда четырехугольник BDFC является:
а) прямоугольником;
б) трапецией;
в) ромбом;
г) параллелограммом.
4. Отрезки АВ и CD – диаметры окружности. Тогда четырехугольник BDAC является:
а) прямоугольником;
б) квадратом;
в) ромбом;
г) параллелограммом.

5. В параллелограмме ABCD сумма двух углов равна 132°. Определите градусную меру углов параллелограмма.

6. Дана равнобокая трапеция ABCD, О – точка пересечения ее диагоналей. Укажите хотя бы одну пару равных треугольников.

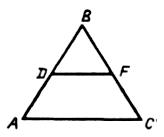
7. В равностороннем треугольнике ABC проведена средняя линия DF. Вычислите периметр четырехугольника ADFC, если периметр FBD равен 27 см.
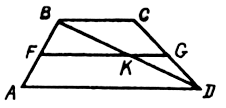
8. В трапеции ABCD средняя линия FG равна 8 см, а основание AD – 12 см. Она пересекает диагональ BD в точке К, тогда отрезок КG равен:
а) 6 см; б) 4 см;
в) 2 см; г) 10 см.
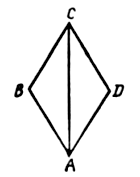
9. Большая диагональ ромба делит его на два равных треугольника. Эти треугольники являются по сторонам: а) разносторонними; б) равносторонними; в) равнобедренными; по углам: а) остроугольными; б) прямоугольными; в) тупоугольными.
Вариант II.
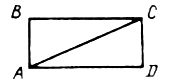
1. Периметр прямоугольника ABCD равен 34 см, а его диагональ АС – 13 см. Найдите периметр ABD.
2. Периметр ромба равен 36 см. Найдите его сторону.
3. Отрезки BF и DC точкой пересечения делятся пополам. Тогда четырехугольник BDFC является: а) прямоугольником; в) ромбом; г) параллелограммом.
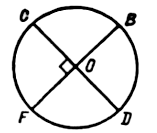
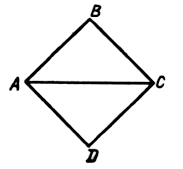
4. Отрезки BF и CD – диаметры окружности, пересекающиеся под прямым углом. Тогда четырехугольник BDFC является: а) прямоугольником; б) квадратом; в) ромбом; г) параллелограммом.
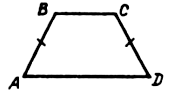
5. В равнобокой трапеции ABCD сумма двух углов равна 212°. Определите градусную меру углов трапеции.
6. Дан параллелограмм ABCD, О – точка пересечения его диагоналей. Укажите хотя бы одну пару равных треугольников.

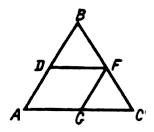
7. В равностороннем треугольнике ABC проведены средние линии FG и DF. Найдите периметр четырехугольника ADFG, если периметр треугольника FBD равен 27 см.
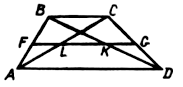
8. В трапеции ABCD с основанием АD = 12 см и ВС = 4 см проведена средняя линия FG. Она пересекает диагональ ВD в точке К, а диагональ АС в точке L, тогда отрезок KL равен: а) 16 см; б) 4 см; в) 8 см; г) 2 см.
9. Диагональ квадрата делит его на два равных треугольника. Эти треугольники являются: по сторонам: а) разносторонними; б) равносторонними; в) равнобедренными; по углам: а) остроугольными; б) прямоугольными; в) тупоугольными.
Ключ к тесту «Четырехугольники»
| 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| I | 24 | 6 | в | а | 114°, 66°, 66°, 114° | АВD = АDС | 45 см | 2 | в, в |
| II | 30 | 6 | г | в | 106°, 106°, 74°, 74° | АDВ= DОС | 36 | 4 | в, б |






























