To'plamlar va ular ustida amallar

Matematika

Mavzu: To‘plamlar va mantiqqa doir masalalar

1-dars: To‘plamlar va ular ustida bajariladigan amallar. Venn diagrammasi

DARSNING MAQSADI

M1 . To‘plam va uning elementlariga doir masalalar yechish

M2 . To‘plamlarning birlashmasi, kesishmasi va ayirmasini topishga doir masalalar yechish

M3 . To‘plamning qism to‘plamlarini topish

M4 . To‘plamlarni Venn diagrammalari yordamida tasvirlash va u asosida masalalar yechish.

To‘plam va uning elementlari

To‘plam deganda ixtiyoriy obyektlarning ( narsalar va predmetlarning) majmuasi tushuniladi va bu obyektlar uning elementlari deb ataladi.

Masalan: Juft sonlar to‘plami, haqiqiy sonlar to‘plami. To‘plamlar A, B, C, … bilan belgilanadi. Elementlari a, b, c, … bilan belgilanadi.

A to‘plamning elementlari soni.

Birorta ham elementga ega bo‘lmagan to‘plam bo‘sh to‘plam deyiladi va Ø kabi belgilanadi

yozuv - x A to‘plamning elementi yoki A to‘plamga tegishli ekanligini,

yozuv - x A to‘plamga tegishli emasligini bildiradi.

To‘plam va uning elementlari

Odatda to‘plamlar ikki xil usulda beriladi .

1- usul . To‘plamning barcha elementlari beriladi:

A = {3; 5; 7; 9;11}, B= {oq, qora, ko‘k},

C = { a ; b ; c }

2- usul. To‘plamning xossalari ko‘rsatiladi:

C= { c : c 10, c N },

X ={ x: x 2 - 8 = 0, x R },

Y ={ y: -4 y 8, y Z }.

1,2,3,5,6,10,15,30. 40 ning bo‘luvchilari = 1,2,4,5,8,10,20,40. P = {1,2,3,5,6,10,15,30} va Q = {1,2,4,5,8,10,20,40} Javob: P ∪ Q = {1,2,3,4,5,6,8,10,15,20,30,40} " width="640"

To‘plamlarning birlashmasi

A va B to‘plamlarning birlashmasi deb, shunday to‘plamga aytiladiki, bu to‘plamning elementlari yoki A to‘plamda, yoki B to‘plamda yotadi.

A va B to‘plamlarning birlashmasi A ∪ B kabi belgilanadi.

1-Masala

P = {30 ning bo‘luvchilari} va Q = {40 ning bo‘luvchilari} bo‘lsin. P ∪ Q ni toping?

Yechish: 30 ning bo‘luvchilari = 1,2,3,5,6,10,15,30.

40 ning bo‘luvchilari = 1,2,4,5,8,10,20,40.

P = {1,2,3,5,6,10,15,30} va Q = {1,2,4,5,8,10,20,40}

Javob: P ∪ Q = {1,2,3,4,5,6,8,10,15,20,30,40}

1,2,3,5,6,10,15,30. 40 ning bo‘luvchilari = 1,2,4,5,8,10,20,40. P = {1,2,3,5,6,10,15,30} va Q = {1,2,4,5,8,10,20,40} Javob: P ⋂ Q = {1,2,5,10} " width="640"

To‘plamlarning kesishmasi

A va B to‘plamlarning kesishmasi deb, shunday to‘plamga aytiladiki, bu to‘plamning elementlari ham A to‘plamga ham B to‘plamga tegishli bo’ladi.

A va B to‘plamlarning kesishmasi kabi belgilanadi.

2-Masala

P = {30 ning bo‘luvchilari} va Q = {40 ning bo‘luvchilari} bo‘lsin. P ⋂ Q ni toping?

Yechish: 30 ning bo‘luvchilari = 1,2,3,5,6,10,15,30.

40 ning bo‘luvchilari = 1,2,4,5,8,10,20,40.

P = {1,2,3,5,6,10,15,30} va Q = {1,2,4,5,8,10,20,40}

Javob: P ⋂ Q = {1,2,5,10}

1,2,3,5,6,10,15,30. 40 ning bo‘luvchilari = 1,2,4,5,8,10,20,40. P = {1,2,3,5,6,10,15,30} va Q = {1,2,4,5,8,10,20,40} Javob: P \ Q = {3, 6, 15, 30} " width="640"

To‘plamlarning ayirmasi

A va B to‘plamlarning ayirmasi deb, A ning B ga tegishli bo‘lmagan barcha elementlaridan tuzilgan to‘plamga aytiladi.

A va B to‘plamlarning ayirmasi A B kabi belgilanadi.

3-Masala

P = {30 ning bo‘luvchilari} va Q = {40 ning bo‘luvchilari} bo‘lsin. P \ Q ni toping?

Yechish: 30 ning bo‘luvchilari = 1,2,3,5,6,10,15,30.

40 ning bo‘luvchilari = 1,2,4,5,8,10,20,40.

P = {1,2,3,5,6,10,15,30} va Q = {1,2,4,5,8,10,20,40}

Javob: P \ Q = {3, 6, 15, 30}

Masalalar yechish

4-Masala

A = {1;2;3;4}, C  { x : x = 2 n - 1, n A } bo‘lsa, A ⋂ C to‘plamni aniqlang?

A) {1; 3;4} B) {1; 3} C) {1; 2;3} D) {1; 2;4}

Yechish: C to‘plamning elementlarini aniqlashtiramiz:

2 n – 1 dagi n ning o‘rniga A to‘plamning elementlarini qo‘yamiz. Natijada , C ={1, 3, 5, 7 } hosil bo‘ladi. U holda

A = {1;2;3;4}, C ={1,3,5,7 } bo’lib, A⋂C= {1,3} bo‘ladi.

Javob: B) A ⋂ C = {1,3}

Masalalar yechish

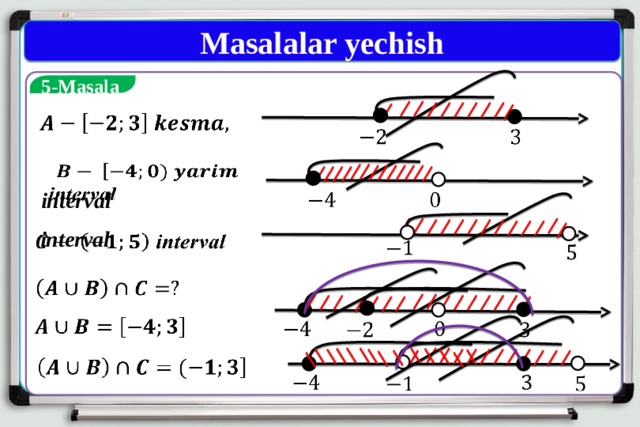
5-Masala

interval

interval

To‘plamning qism to‘plamlari

Agar A to‘plamning hamma elementlari B to‘plamga tegishli bo‘lsa, A to‘plam B to‘plamning qism to‘plami deyiladi va A ⊆ B kabi yoziladi. Bunday holatda “ A to‘plam B da yotadi” yoki “ A to‘plam B ning qismi” deb ham yuritiladi.

Masalan, {2, 3, 5} {1, 2, 3, 4, 5, 6}, chunki, birinchi to‘plamning hamma elementlari ikkinchi to‘plamning ham elementlari bo‘ladi.

• { a } to‘plam ∅ va { a } , ya’ni ( 2 1 ) ikkita qism to‘plamlarga ega.

• { a, b } to‘plam esa ( 2 2 ) to‘rtta: ∅, { a }, { b } va { a, b } qism to‘plamlarga ega.

A ={ a 1 , a 2 , a 3 , a 4 , … , a n -1 , a n } - n ta elementdan iborat bo‘lgan to‘plamning qism to‘plamlar soni 2 n ga teng bo‘ladi.

Masalalar yechish

6-Masala

A , B va C to‘plamlarning elementlari soni mos ravishda

10; 12 va 15 ta. A ∪ B ∪ C to‘plamning elementlari soni eng kamida nechta bo‘la oladi?

A) 22 B) 27 C) 12 D) 15

Yechish : To‘plamlar birlashmasining elementlari soni eng kam bo‘lishi uchun to‘plamlarning biri ikkinchisining qismi bo‘lishi kerak.

A ∪ B ∪ C to‘plamning elementlari soni eng kam bo‘lishi uchun A , B C shart bajarilishi kerak. U holda

C bo‘ladi, yani C) = 15

Javob: D) 15

Masalalar yechish

7-Masala

Agar A to‘plamga 1 ta element qo‘shilgandagi qism to‘plamlar soni A to‘plamdan 1 ta chiqarilib tashlangandagi qism to‘plamlari sonidan 24 taga ko‘p bo‘lsa, A to‘plamning qism to‘plamlar sonini toping.

A) 32 B) 8 C) 4 D) 16

Yechish:

A ={ a 1 , a 2 , a 3 , a 4 , … a n -1 , a n } to‘plamning qism to‘plamlar soni

B ={ a 1 , a 2 , a 3 , a 4 , … a n -1 , a n , a n +1 } qism to‘plamlar soni

C ={ a 1 , a 2 , a 3 , a 4 , … , a n-1 } qism to‘plamlar soni ga teng. Unda

,

Javob: D) 16

Venn diagrammasi

To‘plamlarni Venn diagrammalari yordamida tasvirlash maqsadga muvofiq. Venn diagrammasida U universal to‘plam − to‘g‘ri to‘rtburchak, to‘plam esa shu to‘rtburchak ichida yotgan doira kabi tasvirlanadi.

Masalan, rasmda U universal

to‘plam ichida A to‘plam

tasvirlangan. Doira tashqarisidagi bo‘yalgan soha A to‘plamning to‘ldiruvchisi deyiladi va kabi belgilanadi.

A

U

Venn diagrammasi

A

B

+

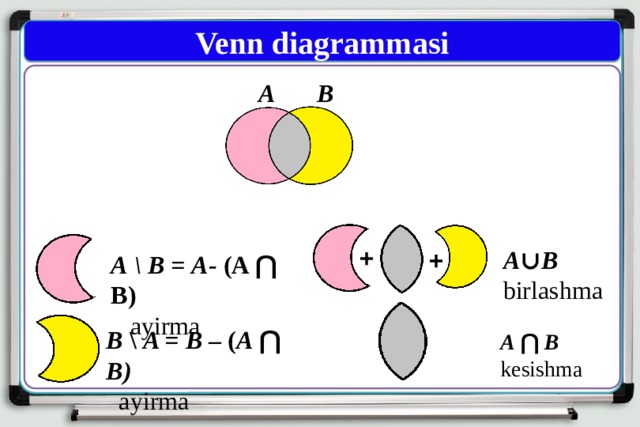
A ∪ B

birlashma

+

А \ В = A- (A ⋂ B)

ayirma

B  \  A = B – ( A ⋂ B)

ayirma

A ⋂ B

kesishma

A ∪ B to‘plamning C to‘plam bilan kesishmasi. ( A ∪ B ) ⋂ C = { a, c, d, f } Javob: D) {a, c,d,f } " width="640"

a, c,d,f

Venn diagrammasi

B

8-Masala

A

Rasmda A , B va C to‘plamlar tasvirlangan. ( A ∪ B ) ⋂ C to‘plamning elementlarini aniqlang.

A) { a, b, c, d, g, h, f } B) { a, b, c, d, g, f }

C) { a, b, c, d } D) { a, c, d, f }

C

Yechish : Rasmga ko‘ra:

A ∪ B = {i, j, k, b, a, f, c, d, g, h}

C = {f, a, c, d, e}

( A ∪ B ) ⋂ C = A ∪ B to‘plamning C to‘plam bilan kesishmasi. ( A ∪ B ) ⋂ C = { a, c, d, f }

Javob: D) {a, c,d,f }

Masalalar yechish

9-Masala

100 kishidan iborat sayyohlar guruhidan 60 % i ingliz tilini, 50 % i fransuz tilini, 17 % i esa har ikkala tilni ham biladi. Necha nafar sayyoh ingliz tilini ham, fransuz tilini ham bilmaydi?

A) 11 B) 8 C) 6 D) 7

Yechish:

Javob: D) 7

50 %

60 %

17 %

Masalalar yechish

10-Masala

30 nafar o‘quvchidan 3 x +1 nafari rus tilini , 2 x -1 nafari ingliz tilini, x -1 nafari rus tilini ham ingliz tilini ham biladi. 5 nafari esa, rus tilini ham ingliz tilini ham bilmaydi. Necha nafar o‘quvchi rus tilini biladi?

A) 13 B) 19 C) 11 D) 17

Yechish:

Javob: B) 19

2x-1

x-1

3x+1

MUSTAQIL BAJARISH UCHUN TOPSHIRIQlAR

1. (M1,M3) a element A = { a; b; c; d; e;f } to‘plamning nechta qism to‘plamiga tegishli bo‘ladi?

A) 16 B) 8 C) 32 D) 64

2. (M3) A = {a; b; c; d; e; f} to‘plamning elementlari soni 2 ta bo‘lgan nechta qism to‘plami bor?

A) 15 B) 4 C) 8 D) 16

3. (M1) A to‘plam 48 sonining butun bo‘luvchilaridan tashkil topgan bo‘lsa, A to‘plamning elementlari sonini aniqlang.

A) 20 B) 18 C) 10 ; D) 16

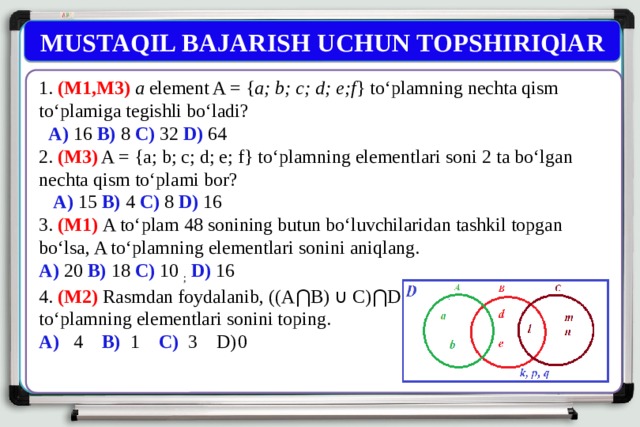
4. (M2) Rasmdan foydalanib, ((A⋂B) ∪ C)⋂D

to‘plamning elementlari sonini toping.

A) 4 B) 1 C) 3 D) 0

4, x R } bo‘lsa, A ⋂ В to‘plamni aniqlang. A) [2; 8] B) {3; 4; 5; 6; 7; 8} C) {2; 3; 4; 5; 6; 7; 8} D) (2; 8] " width="640"

MUSTAQIL BAJARISH UCHUN TOPSHIRIQlAR

5. (M2, M4) Rasmda A va В to‘plamlar va U universial to‘plam tasvirlangan. Quyidagi to‘plamlardan qaysi biri bo‘yalgan sohaga mos to‘plamni tasvirlaydi?

(A'= U \A; B'= U\B)

A) (А⋂В')∪(А'⋂В) B) (А'⋂В')∪(А⋂В)

C) (A ⋂ B') ∪ (A ⋂ B) D) (А '⋂ В) ∪ (А ⋂ В)

6. (M1,M2) A = {(x, y) x 2 + у 2 = 4; x,y R},

В = {( x, у ) x - у = 2; x,y R} bo‘lsa, A ⋂ В to‘plamni aniqlang.

A) {(-2; 0); (0; 2)} B) {(2; 0); (0; 2)} C) {(2; 0); (0; -2)} D) {(-2; 0); (0; -2)}

7. (M1,M2) Agar A = { x x 2 x R },

В = { x x 2 4, x R } bo‘lsa, A ⋂ В to‘plamni aniqlang.

A) [2; 8] B) {3; 4; 5; 6; 7; 8} C) {2; 3; 4; 5; 6; 7; 8} D) (2; 8]

MUSTAQIL BAJARISH UCHUN TOPSHIRIQlAR

8. (M1) A = { x | x 2, x Z } to‘plamning Z to‘plamgacha to‘ldiruvchi A ' to‘plamini toping. ( A ' = Z \ A )

A) A ' = { x | x 2, x Z } B) A '= { x | x Z }

C) A ' = { x | x 1, x Z } D) A ' = { x | x x Z}

9. (M1) A = { =0, x Z } to‘plamga teng bo‘lgan to‘plamni aniqlang.

A) { x xn = 0, nN } B) { xx = k , к N }

C) { xx = , R } D) { x x = n , n Z }

10. (M1) va B A. A va В to‘plamlarning elementlari soni mos ravishda m va n ga teng. Agar n + 3m = 18 bo ’ lsa, A to‘plamning elementlari sonini toping.

A ) 3 B) 2 C) 5 D) 4

DARSNI YAKUNLASH

Bugungi darsda to‘plamlar, to‘plamlarning elementlari, berilish usullari, to‘plamlarni birlashmasi, kesishmasi, ayirmasini, qism to‘plamlarini topishni, qolaversa Venn diagrammasida to‘plamlarni tasvirlashni

o‘rgandik.

Venn diagrammasi yordamida to‘plamlarni tasvirlash eng samarali va ko‘rgazmali usul hisoblanadi.

FOYDALANILGAN ADABIYOTLAR RO‘YXATI

• M.A. Mirzaahmedov, Sh.N. Ismailov, A.Q. Amanov,

B.Q.Xaydarov, Matematika 10, darslik, Toshkent, 2017.

• R.N.Nazarov va boshqalar Algebra va sonlar nazariyasi,

1-qism Toshkent, 1993.

• MATEMATIKA 2019-yil test topshiriqlari, Davlat Test

Markazi, Toshkent, 2019.

TAQDIMOTNI TAYYORLAGANLAR:

ARALASHMAGA OID MASALALAR

1. T.Umirzakov – Samarqand viloyati Ishtixon tumanidagi 1-IDUM matematika fani o‘qituvchisi; 2. M.Komilov – Toshkent shahar XTV tasarrufidagi AFIDUM matematika fani o‘qituvchisi. Taqdimot Toshkent shahar XTXQTUMOHM professori B. Xaydarov umumiy tahriri ostida tayyorlandi.

E’TIBORINGIZ UCHUN RAHMAT

Muloqot uchun manzil:

@aljabrmo – telegramm kanali,

aljabrrobot – telegramm boti