ЕГЭ геометрия 2
1.На клетчатой бумаге с размером клетки 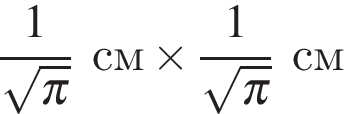 изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.



2. На клетчатой бумаге с размером клетки 1 1 изображён угол. Найдите тангенс этого угла.
1 изображён угол. Найдите тангенс этого угла.
3. В треугольнике ABC AC = BC = 6, высота AH равна 3. Найдите угол C. Ответ дайте в градусах.
4.В треугольнике 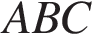 угол
угол  равен
равен  ,
, 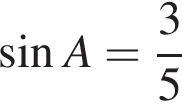 ,
, 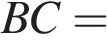 3,
3,  — высота. Найдите
— высота. Найдите 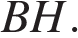
5. В правильной треугольной пирамиде 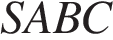 медианы основания пересекаются в точке
медианы основания пересекаются в точке  Площадь треугольника
Площадь треугольника 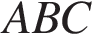 равна 13, объем пирамиды равен 52. Найдите длину отрезка
равна 13, объем пирамиды равен 52. Найдите длину отрезка 
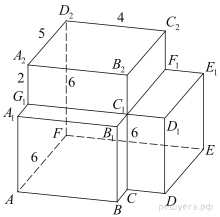
6. Найдите угол 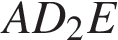 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
7. В прямоугольном параллелепипеде ABCDA1B1C1D1 через диагональ BD1 проведена плоскость α, параллельная прямой AC.
а) Докажите, что прямая пересечения плоскости α с плоскостью основания A1B1C1D1 параллельна прямой A1C1.
б) Найдите угол между проведённой плоскостью и плоскостью основания параллелепипеда, если AB = 5, BC = 12, CC1 = 10.
8. Длина ребра правильного тетраэдра ABCD равна x. M — середина ребра BC, L — середина ребра AB.
а) Докажите, что плоскость, содержащая прямую DM и параллельная прямой CL, делит ребро AB в отношении 3:1, считая от вершины A.
б) Найдите угол между прямыми DM и CL.
ЕГЭ геометрия 3
1.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.


2. На клетчатой бумаге с размером клетки 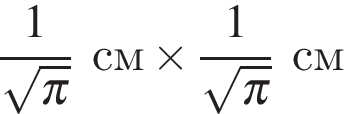 изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
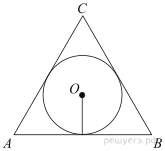
3. Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
4.Площадь ромба равна 867. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.
5. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 16, а площадь боковой поверхности равна 168. Найдите длину отрезка AB.
6. Радиусы трех шаров равны 2, 12 и 16. Найдите радиус шара, объем которого равен сумме их объемов.
7. Все рёбра правильной треугольной пирамиды SBCD с вершиной S равны 18.
Основание O высоты SO этой пирамиды является серединой отрезка SS1, M — середина ребра SB , точка L лежит на ребре CD так, что CL : LD = 7 : 2.
а) Докажите, что сечение пирамиды SBCD плоскостью S1LM — равнобокая трапеция.
б) Вычислите длину средней линии этой трапеции.
8. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.
а) Докажите, что плоскость CEF параллельна ребру SB .
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.


























