Вариант № 1537
1. Найдите значение выражения: 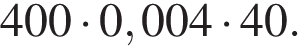
2. Одно из чисел 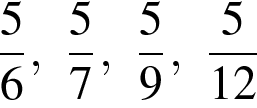 отмечено на координатной прямой точкой
отмечено на координатной прямой точкой 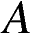 . Укажите это число.
. Укажите это число.
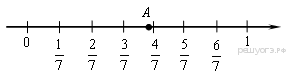
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 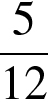
3. Какое из данных ниже выражений при любых значениях 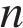 равно дроби
равно дроби 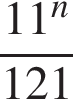 ?
?
1) 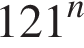
2) 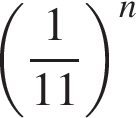
3) 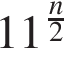
4) 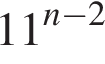
4. Решите уравнение 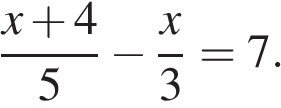
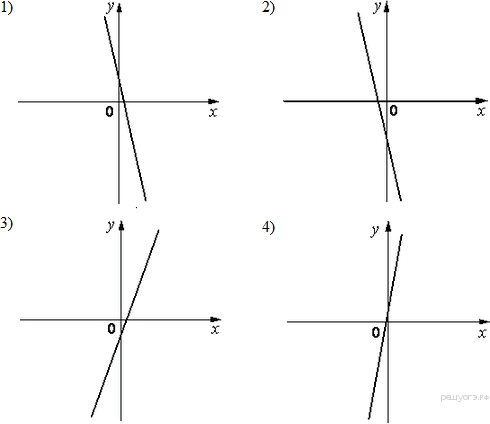
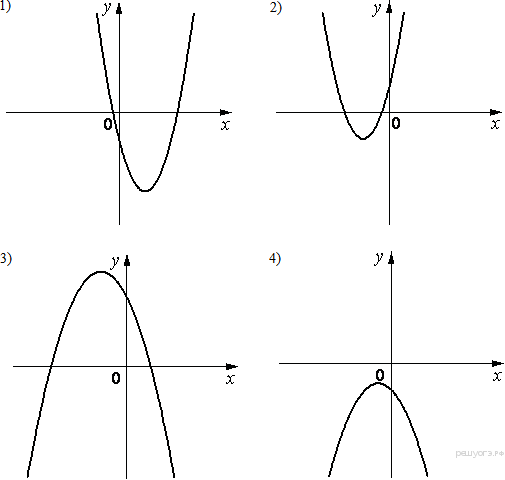
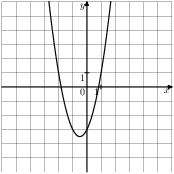
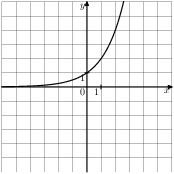
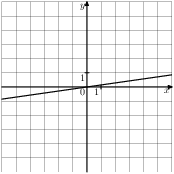
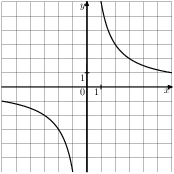
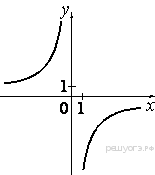
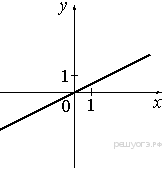
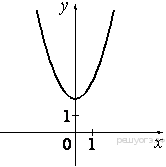
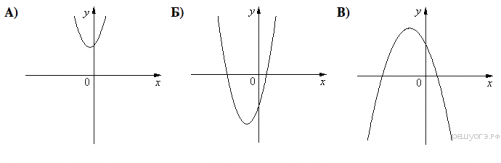
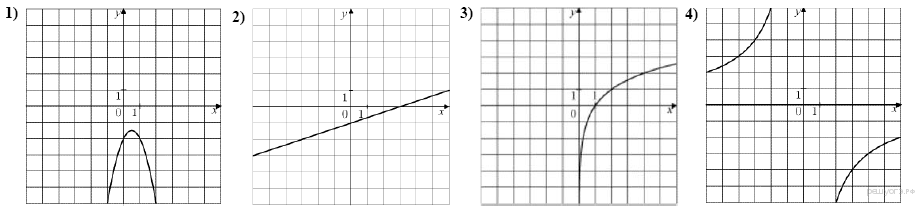
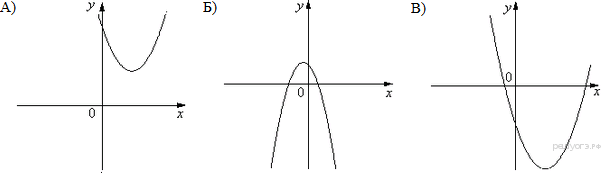
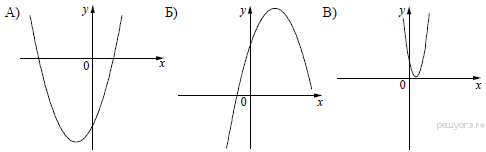
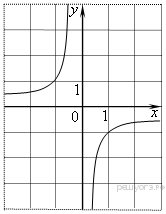
5. На одном из рисунков изображена парабола. Укажите номер этого рисунка.
6. Дана арифметическая прогрессия (an), для которой a5 = 71, a11 = 149. Найдите разность прогрессии.
7. Найдите значение выражения 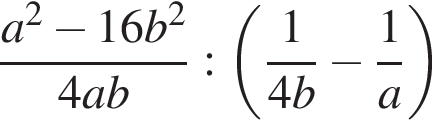 при
при 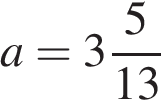 и
и 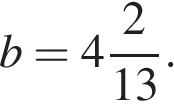
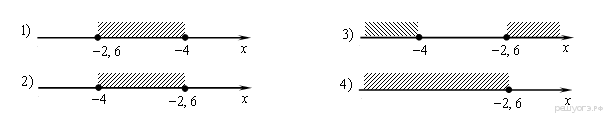
8. Решите систему неравенств
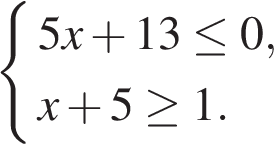
На каком рисунке изображено множество её решений?
В ответе укажите номер правильного варианта.
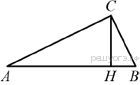
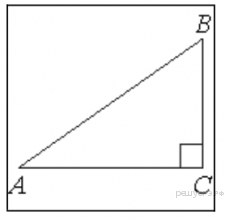
9. В прямоугольном треугольнике ABC катет AC = 90, а высота CH, опущенная на гипотенузу, равна 72. Найдите 
 .
.
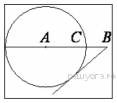
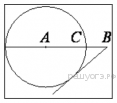
10. На отрезке 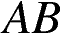 выбрана точка
выбрана точка  так, что
так, что 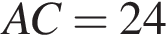 и
и  . Построена окружность с центром
. Построена окружность с центром 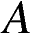 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 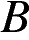 к этой окружности.
к этой окружности.
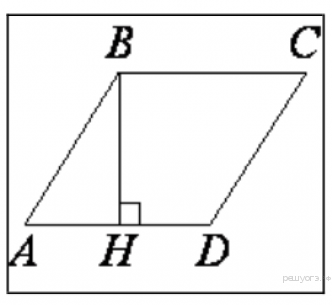
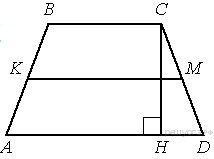
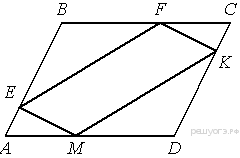
11. Высота 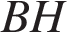 ромба
ромба 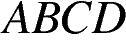 делит его сторону
делит его сторону  на отрезки
на отрезки  и
и  . Найдите площадь ромба.
. Найдите площадь ромба.
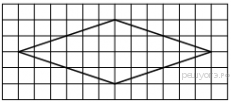
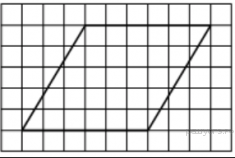
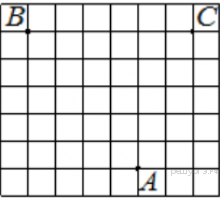
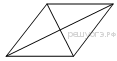
12. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
13. Какое из следующих утверждений верно?
1. Диагонали ромба равны.
2. Отношение площадей подобных треугольников равно коэффициенту подобия.
3. Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
14. В таблице даны результаты олимпиад по русскому языку и биологии в 9 «А» классе.
| Номер ученика | Балл по русскому языку | Балл по биологии |
| 5005 | 93 | 38 |
| 5006 | 70 | 92 |
| 5011 | 97 | 36 |
| 5015 | 50 | 90 |
| 5018 | 30 | 92 |
| 5020 | 49 | 93 |
| 5025 | 94 | 70 |
| 5027 | 47 | 55 |
| 5029 | 81 | 65 |
| 5032 | 66 | 32 |
| 5041 | 60 | 81 |
| 5042 | 41 | 47 |
| 5043 | 88 | 89 |
| 5048 | 99 | 79 |
| 5054 | 69 | 36 |
Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 140 или хотя бы по одному предмету набрано не меньше 75 баллов. Сколько человек из 9 «А», набравших меньше 75 баллов по русскому языку, получат похвальные грамоты?
1) 5
2) 4
3) 2
4) 3
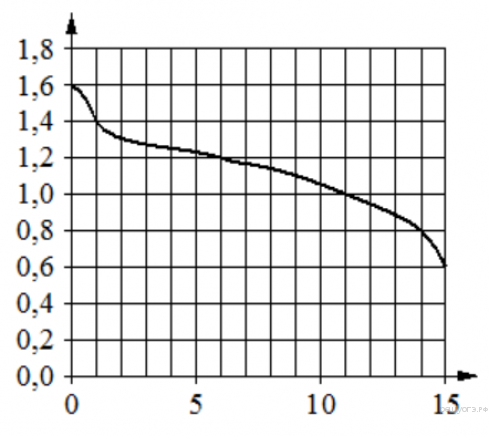
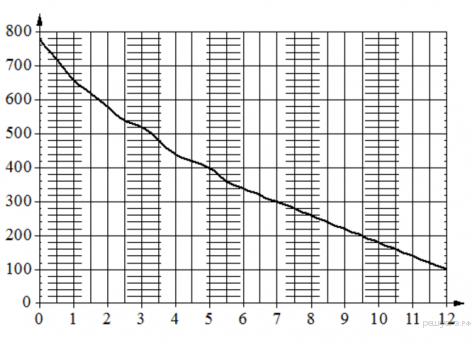
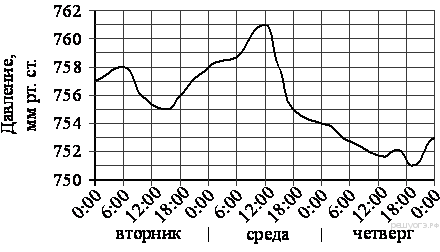
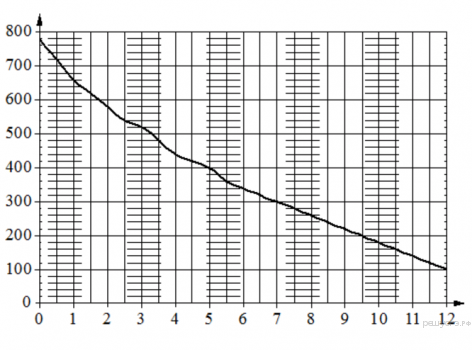
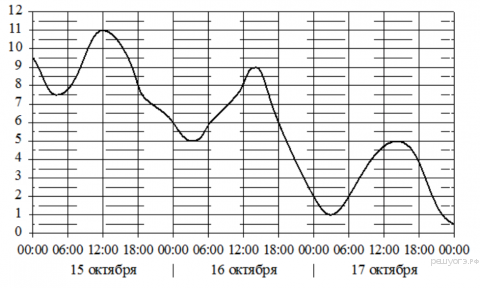
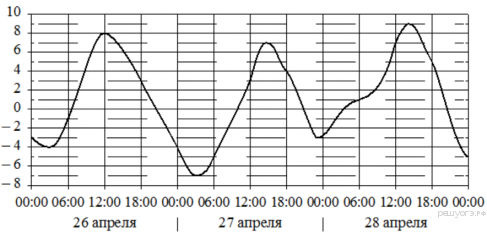
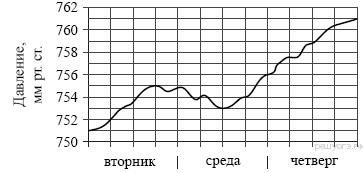
15. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси - напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 11 часов работы фонарика.
16. В начале года число абонентов телефонной компании «Восток» составляло 800 тыс. человек, а в конце года их стало 880 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
17. Сколько спиц в колесе, если угол между соседними спицами равен 24°?
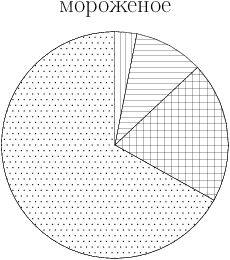
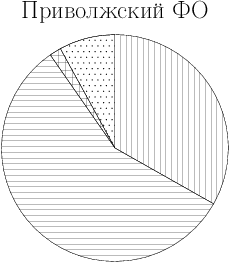
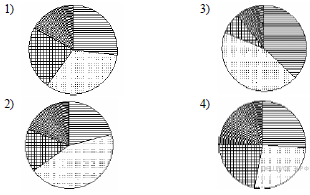
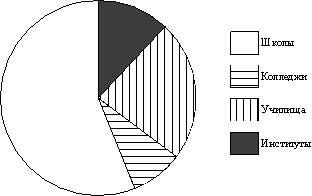
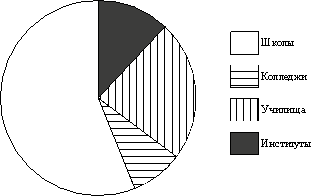
18. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.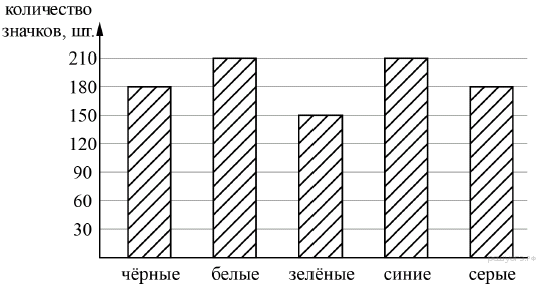
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5
2) 10
3) 15
4) 20
19. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
20. Полную механическую энергию тела (в джоулях) можно вычислить по формуле  где
где  — масса тела (в килограммах),
— масса тела (в килограммах), 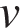 — его скорость (в м/с),
— его скорость (в м/с), 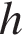 — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а
— высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а 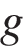 — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите
— ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите 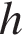 (в метрах), если а
(в метрах), если а
21. Сократите дробь .
22. От пристани А к пристани В, расстояние между которыми равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью, на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
23. Постройте график функции
и определите, при каких значениях  прямая
прямая  имеет с графиком одну или две общие точки.
имеет с графиком одну или две общие точки.
24. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
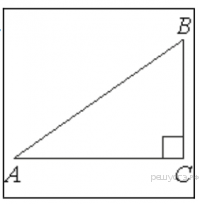
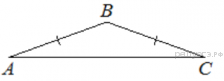
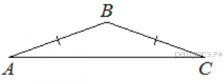
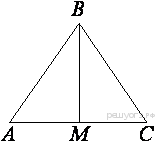
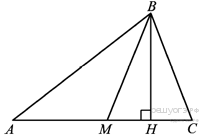
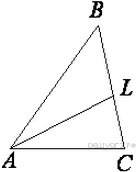
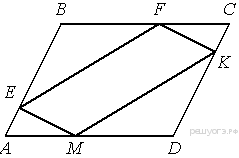
25. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
26. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC.
21. Сократите дробь .
Решение.
Используем свойства степеней:
Ответ: 96.
22. От пристани А к пристани В, расстояние между которыми равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью, на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
Решение.
Пусть  км/ч — скорость первого теплохода, тогда
км/ч — скорость первого теплохода, тогда  км/ч — скорость второго теплохода. Расстояние между пристанями 70 км, второй теплоход отправился в путь через час после выхода первого, причём в конечный пункт оба теплохода прибыли одновременно, составим уравнение:
км/ч — скорость второго теплохода. Расстояние между пристанями 70 км, второй теплоход отправился в путь через час после выхода первого, причём в конечный пункт оба теплохода прибыли одновременно, составим уравнение:
Корень −28 не подходит по условию задачи, следовательно, скорость первого теплохода равна 20 км/ч.
Ответ: 20.
23. Постройте график функции
и определите, при каких значениях  прямая
прямая  имеет с графиком одну или две общие точки.
имеет с графиком одну или две общие точки.
Решение.
Построим график функции при  и график функции при
и график функции при 
Прямая  имеет с графиком одну или две общие точки при
имеет с графиком одну или две общие точки при  и при
и при 
Ответ:
24. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Решение.
Из треугольника найдем
 — биссектриса, следовательно,
— биссектриса, следовательно,
Треугольник  — прямоугольный, следовательно:
— прямоугольный, следовательно:
Найдём угол
Ответ: 20°.
25. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
Решение.
Треугольник  — равнобедренный, следовательно, . Углы
— равнобедренный, следовательно, . Углы  и
и  — развёрнутые, поэтому:
— развёрнутые, поэтому:
Рассмотрим треугольники  и следовательно, эти треугольники равны, а значит, то есть треугольник
и следовательно, эти треугольники равны, а значит, то есть треугольник  — равнобедренный.
— равнобедренный.
26. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC.
Решение.
Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. AQ и AO — биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AM2 = MQ · MO. Следовательно,
Ответ: 4,5.
№ п/п Номер Тип Ваш ответ Правильный ответ
1 316366 1 Не решено 64
2 311392 2 Не решено 3
3 350334 3 Не решено 4
4 338555 4 Не решено -46,5
5 193097 5 Не решено 1
6 353085 6 Не решено 13
7 340918 7 Не решено 20
8 311672 8 Не решено 2
9 351333 9 Не решено 0,6
10 349996 10 Не решено 32
11 351995 11 Не решено 540
12 352579 12 Не решено 30
13 352932 13 Не решено 3
14 351652 14 Не решено 1
15 351326 15 Не решено 0,6
16 341387 16 Не решено 10
17 341123 17 Не решено 15
18 316379 18 Не решено 3
19 132744 19 Не решено 0,6
20 316355 20 Не решено 5
21 47 21 (C1) Набрано баллов: 0
22 338967 22 (C2) Набрано баллов: 0
23 333320 23 (C3) Набрано баллов: 0
24 315007 24 (C4) Набрано баллов: 0
25 315022 25 (C5) Набрано баллов: 0
26 340603 26 (C6) Набрано баллов: 0







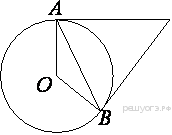 Касательные в точках A и B к окружности с центром O пересекаются под углом 18°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 18°. Найдите угол ABO. Ответ дайте в градусах.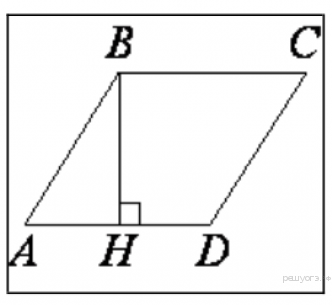
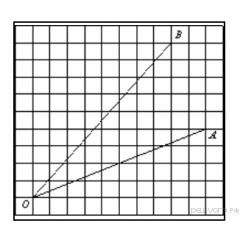
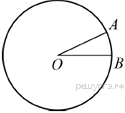
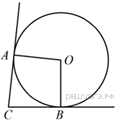
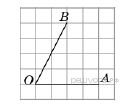 Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображенного на рисунке.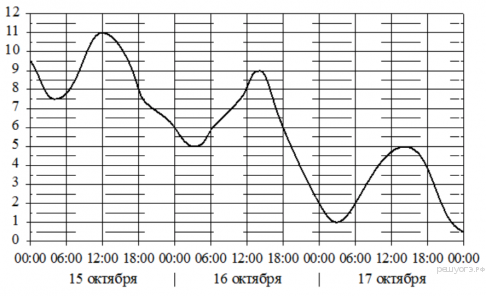


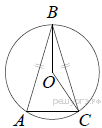 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 79°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 79°. Найдите величину угла BOC. Ответ дайте в градусах.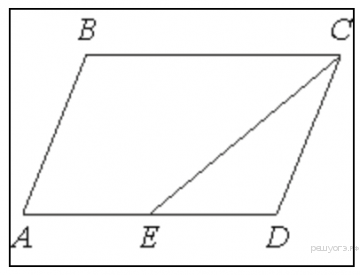
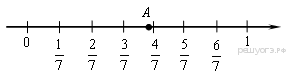
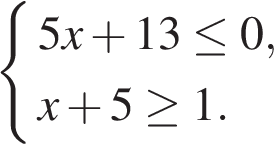







 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что 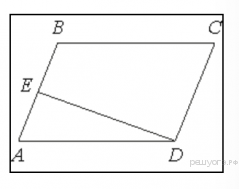
 На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.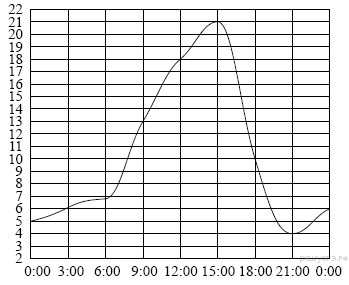
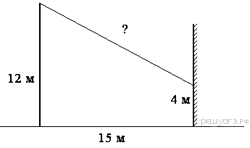
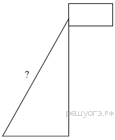
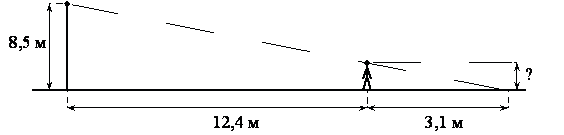 Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8,5 м. Тень человека равна 3,1 м. Какого роста человек (в метрах)?
Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8,5 м. Тень человека равна 3,1 м. Какого роста человек (в метрах)?
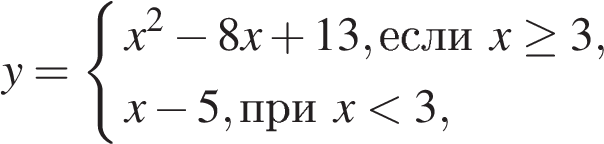
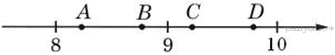
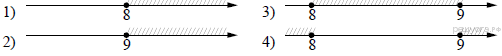
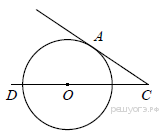
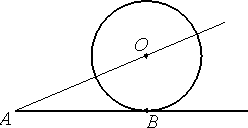 К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 14 , AO = 50 .
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 14 , AO = 50 .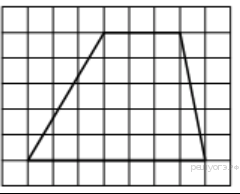

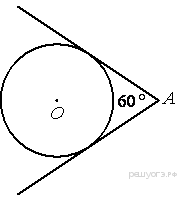 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60° , а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60° , а расстояние от точки А до точки О равно 6.




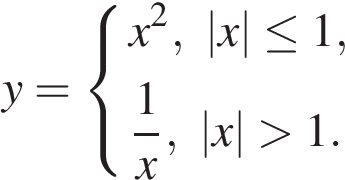

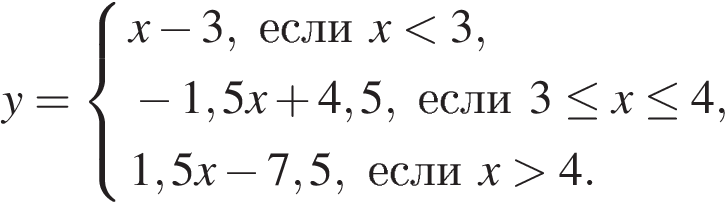
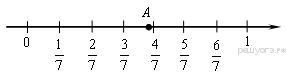
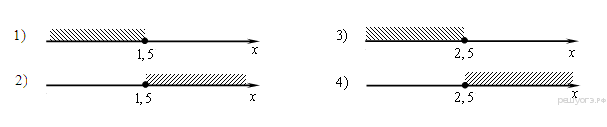
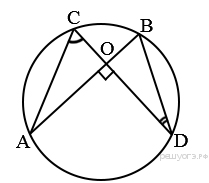 Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.
Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.
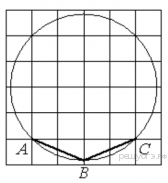
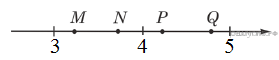
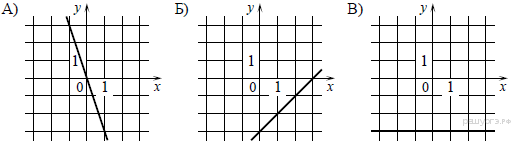
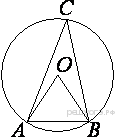 Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.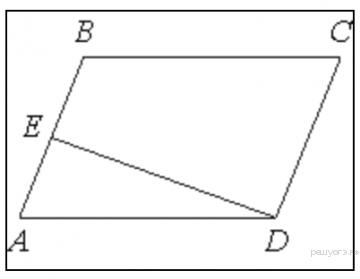
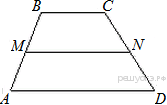
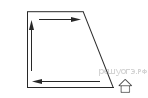
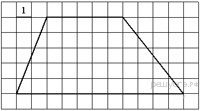 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
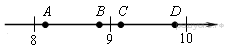
 Найдите площадь ромба, если его диагонали равны 14 и 6.
Найдите площадь ромба, если его диагонали равны 14 и 6.