Тренировочный лист №1
«ОГЭ: задания 16-20, геометрия»
2020 г
Ф. Имя ___________________________________________
| № | Задания | Ответы |
| 1 | На плоскости даны четыре прямые. Известно, что ˪1=120⁰, ˪2=60⁰ , ˪3=55⁰ . Найдите ˪4. Ответ дайте в градусах. 
|
|
| 2 | Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности. 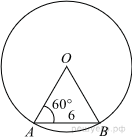
|
|
| 3 | Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры. 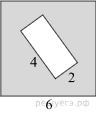
|
|
| 4 | Найдите тангенс угла AOB, изображенного на рисунке. 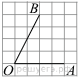
|
|
| 5 | Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой. Если утверждений несколько, запишите их номера в порядке возрастания.
|
|
Ответы:
-
125
-
6
-
28
-
2
-
12
Решение:
1. Так как ˪1 и ˪2, односторонние и их сумма равна 180°, прямые, которые заключают эти углы, — параллельны. Найдем угол, смежный с углом 3: 180⁰-55⁰=125⁰. Этот угол и угол 4 соответственные и равные, так как прямые параллельны. Таким образом, угол 4 = 125°.
Ответ: 125.
2. Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу.
Углы при основании равнобедренного треугольника равны. Пусть AOB равен x, тогда x + 60° + 60° = 180°, где x = 60°. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
Ответ: 6.
3. Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.
Ответ: 28.
4. Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4:2=2
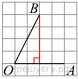
Ответ: 2.
5. Проверим каждое из утверждений.
1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.
2) «Вертикальные углы равны» — верно, это теорема планиметрии.
3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.
Ответ: 12.
Источники:
https://oge.sdamgia.ru/test?theme=20
https://math-oge.sdamgia.ru/test?theme=12
https://math-oge.sdamgia.ru/test?theme=15
https://math-oge.sdamgia.ru/test?theme=95
https://math-oge.sdamgia.ru/test?theme=41
https://math-oge.sdamgia.ru/test?theme=57






























