Основной государственный экзамен по МАТЕМАТИКЕ Тренировочный вариант от 3.03.2025г
Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.
Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если получилась обыкновенная дробь, ответ запишите в виде десятичной. Решения заданий части 2 и ответы к ним запишите на бланке ответов № 2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер. Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки.
Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям. При выполнении части 1 все необходимые вычисления, преобразования выполняйте в черновике.
Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом КИМ, и линейкой. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом КИМ и линейкой.
Для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2 баллов должны быть получены за решение заданий по геометрии (задания 15–19, 23–25).
После завершения работы проверьте, чтобы ответ на каждое задание в бланках ответов № 1 и № 2 был записан под правильным номером.
Желаем успеха!
Часть 1
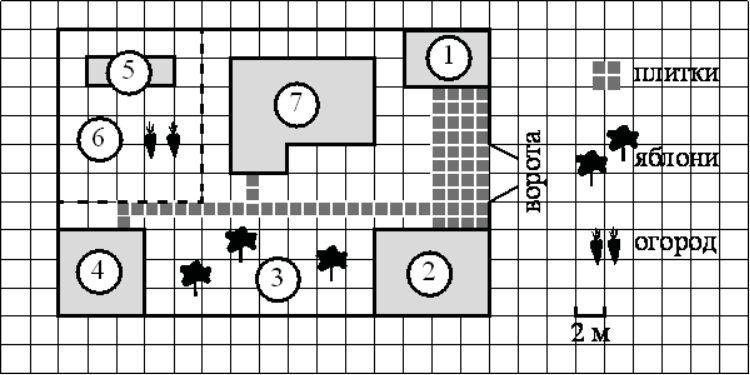
На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м×1 м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
-
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Ответ:
-
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки?
Ответ:
-
Найдите площадь, которую занимает баня. Ответ дайте в квадратных метрах.
-
Найдите значение выражения
a7 a19 : a 23
при a 2 .
Ответ:
Ответ:
-
На сколько процентов площадь, которую занимает теплица, меньше площади, которую занимает гараж?
Ответ:
-
Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
-
Решите уравнение x2 10 x 21 0. Если уравнение имеет более одного корня, то в ответ запишите больший из корней
Ответ:
-
В среднем из 50 карманных фонариков, поступивших в продажу, шесть неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Ответ:
-
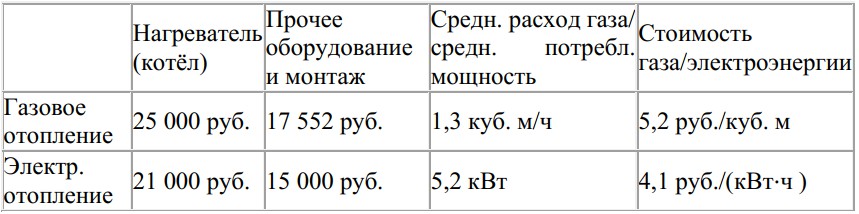 На рисунке изображены графики функций вида y kx b .
На рисунке изображены графики функций вида y kx b .
Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки и установки газового и электрического оборудования?
Ответ:
-
Найдите значение выражения 4, 7 8, 2
Ответ:
-
На координатной прямой отмечены числа p, q и r.
Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
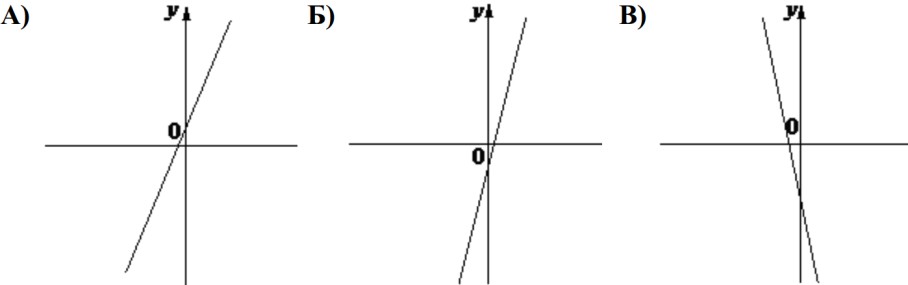
КОЭФФИЦИЕНТЫ
-
 k 0,
k 0,
b 0
-
k 0,
b 0
-
k 0,
b 0
Какая из разностей q p,
r q,
p r
отрицательна?
В таблице под каждой буквой укажите соответствующий номер
-
q p
-
r q
-
p r
-
ни одна из них
Ответ:
-
Сила Архимеда, выталкивающая на поверхность погружённое в воду тело, вычисляется по формуле F gV , где 1000
кг/м3 – плотность воды, g 9,8 м/с2 – ускорение свободного падения, а V – объём тела в кубических метрах. Сила F измеряется в ньютонах. Найдите силу Архимеда, действующую
на погружённое в воду тела объёмом 0,05 куб. м. Ответ дайте в ньютонах.
Ответ:
-
Укажите решение неравенства 3x x2 0
-
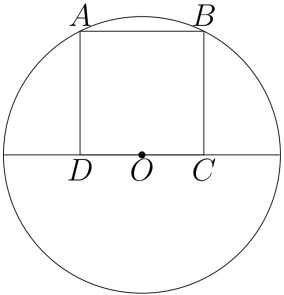
Точка О является серединой стороны CD квадрата ABCD. Радиус окружности с центром в точке O, проходящей через вершину А, равен 1,5. Найдите площадь квадрат ABCD.
 Ответ:
Ответ:
-
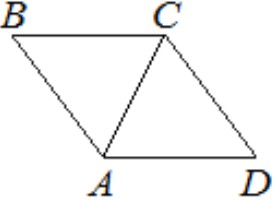 В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
Ответ:
1) 3;
3) 0;
2) ;0 3;
-
0;3
-
 На клетчатой бумаге с размером клетки
На клетчатой бумаге с размером клетки
1×1 изображён ромб. Найдите площадь
Ответ:
-
Каучуковый мячик с силой бросили на асфальт. Отскочив, мячик подпрыгнул на 5,4 м, а при каждом следующем прыжке он поднимался на высоту в три раза меньше предыдущей. При каком по счёту прыжке мячик в первый раз не достигнет высоты 10 см?
 Ответ:
Ответ:
-
В треугольнике ABC угол C равен 90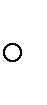 , M –
, M –
этого ромба.
Ответ:
-
Какое из следующих утверждений верно?
-
Отношение площадей подобных треугольников равно коэффициенту подобия.
-
Диагонали прямоугольника точкой пересечения делятся пополам.
-
Биссектриса треугольника делит пополам сторону, к которой проведена.
середина стороны AB, Найдите CM.
AB 20,
BC 10.
В ответ запишите номер выбранного утверждения. Ответ:
Не забудьте перенести в бланк ответов №1 в соответствии с инструкцией по выполнению работы
Ответ:

Модуль «Геометрия»
Часть 2
-
Решите систему уравнений:
Модуль «Алгебра»
9
x2 14
x
y,
9
x 14
y.
-
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 9, CK = 15.
-
Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
-
Окружности с центрами в точках P и Q не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
-
Постройте график функции
x2 8x 17 при
y
x 2 при
x 2,
x 2.
-
Окружности радиусов 33 и 99 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Определите, при каких значениях m прямая y m
графиком две общие точки.
имеет с
 ОТВЕТЫ К ТРЕНИРОВОЧНОМУ ВАРИАНТУ
ОТВЕТЫ К ТРЕНИРОВОЧНОМУ ВАРИАНТУ
| 1 | 7352 |
| 2 | 5 |
| 3 | 36 |
| 4 | 75 |
| 5 | 450 |
| 6 | – 3,5 |
| 7 | 3 |
| 8 | 8 |
| 9 | 7 |
| 10 | 0,88 |
| 11 | 312 |
| 12 | 490 |
| 13 | 4 |
| 14 | 5 |
| 15 | 10 |
| 16 | 1,8 |
| 17 | 70 |
| 18 | 20 |
| 19 | 2 |
| 20 | 1; 5, 14 ; 0 . 9 |
| 21 | 420. |
| 22 | 5; 4 1. |
| 23 | 66. |
| 24 |
|
| 25 | 99. |








 На рисунке изображены графики функций вида y kx b .
На рисунке изображены графики функций вида y kx b .
 Ответ:
Ответ:  В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах. На клетчатой бумаге с размером клетки
На клетчатой бумаге с размером клетки Ответ:
Ответ: 
 ОТВЕТЫ К ТРЕНИРОВОЧНОМУ ВАРИАНТУ
ОТВЕТЫ К ТРЕНИРОВОЧНОМУ ВАРИАНТУ 



















