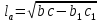ТРЕУГОЛЬНИКИ
Треугольником называется геометрическая фигура, которая состоит из трёх точек – вершин треугольника – и трёх соединяющих их отрезков, – сторон треугольника.
Виды треугольников:
1. Остроугольный. Все углы у него острые.
2. Тупоугольный. Один угол у него тупой, два других – острые.
3. Прямоугольный. Один угол у него прямой, два других – острые.
4. Равнобедренный. Две стороны у него равны.
5. Равносторонний. Все стороны у него равны.
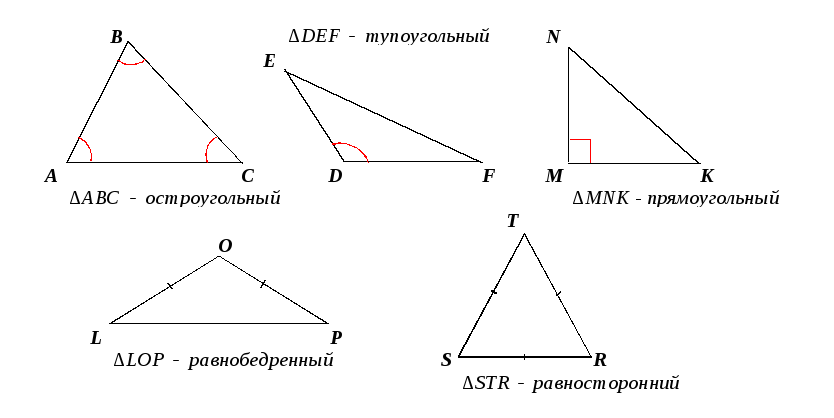
Треугольники называются равными, если у них все соответствующие стороны и углы равны.


ТЕОРЕМА: Если прямая, не проходящая ни через одну вершину треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ.
ТЕОРЕМА: Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ.
ТЕОРЕМА: Если сторона и два прилежащих к ней угла одного треугольника, равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ.
ТЕОРЕМА: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
ТЕОРЕМА: Сумма углов любого треугольника равна 180°.

СЛЕДСТВИЕ: У любого треугольника хотя бы два угла острые.
Внешним углом треугольника называется угол, смежный с углом треугольника при данной вершине.
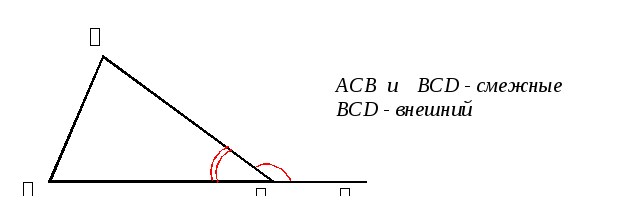
ТЕОРЕМА: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
(Евклидова геометрия)
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Против большей стороны лежит больший внутренний угол.
Против большего внутреннего угла лежит большая сторона.
В любом треугольнике каждая сторона меньше суммы двух других сторон, но больше разности большей и меньшей из оставшихся сторон.

ОПРЕДЕЛЕНИЕ ВИДА ТРЕУГОЛЬНИКА ПО ЕГО СТОРОНАМ
Пусть с – наибольшая сторона треугольника.
Треугольник остроугольный, если  .
.
Треугольник прямоугольный, если 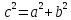 .
.
Треугольник тупоугольный, если  .
.
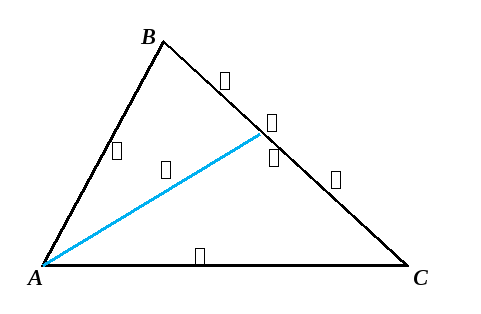
БИССЕКТРИСА ТРЕУГОЛЬНИКА
Биссектрисой треугольника, проведённой из данной вершины называется отрезок, выходящий из вершины данного угла и делящий этот угол пополам.
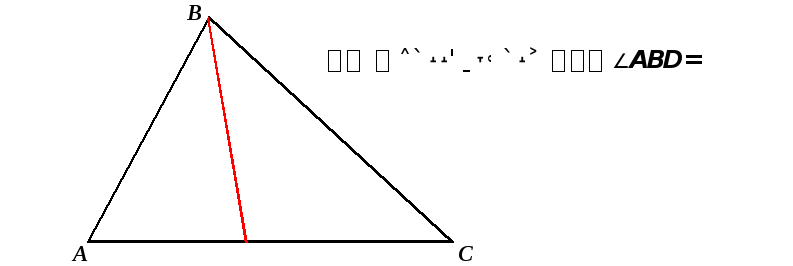
ТЕОРЕМА: Биссектрисы треугольника пересекаются в точке, являющейся центром вписанной в треугольник окружности.
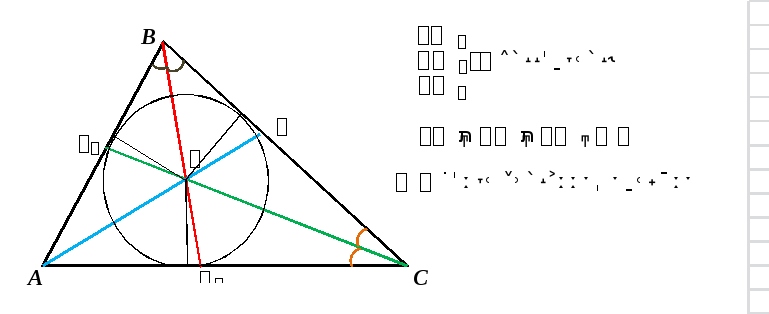
Свойства биссектрис треугольника.
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.
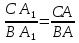 (из рисунка сверху)
(из рисунка сверху)
Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Если  биссектриса к стороне
биссектриса к стороне  , то длина биссектрисы равна:
, то длина биссектрисы равна:
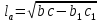
или

МЕДИАНА ТРЕУГОЛЬНИКА
Медианой треугольника, проведённой из данной вершины называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника.

ТЕОРЕМА: Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

Свойства медиан треугольника.
Медиана разбивает треугольник на два равновеликих треугольника (т.е. на треугольники с одинаковой площадью).
Весь треугольник разбивается своими медианами на шесть равновеликих треугольников.
Если медиана к стороне  , то длина медианы равна:
, то длина медианы равна:
или
ВЫСОТА ТРЕУГОЛЬНИКА
Высотой треугольника, проведённой из данной вершины называется отрезок, выходящий из данной вершины перпендикулярно (под углом 90°) противолежащей стороне.
Свойства медиан треугольника.
В остроугольном треугольнике высоты пересекаются внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – в вершине прямого угла.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Если высота к стороне  ,
,  – полупериметр треугольника, то длина высоты равна:
– полупериметр треугольника, то длина высоты равна:
3


















 .
.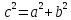 .
. .
.

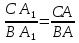 (из рисунка сверху)
(из рисунка сверху)
 биссектриса к стороне
биссектриса к стороне  , то длина биссектрисы равна:
, то длина биссектрисы равна: