ТРЕУГОЛЬНИКИ
ТЕОРЕМА ЧЕВЫ: Для того, чтобы прямые 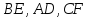 пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство:
пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство: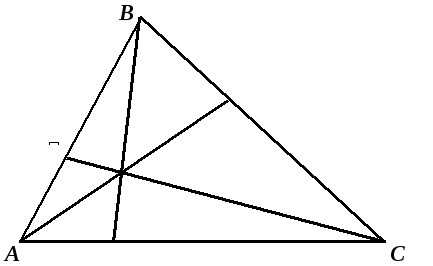
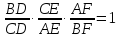
ТЕОРЕМА СИНУСОВ
Если 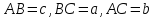 ,
, 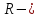 радиус описанной окружности, то
радиус описанной окружности, то
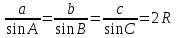
ТЕОРЕМА КОСИНУСОВ
Если 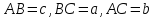 , то
, то

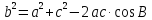
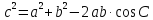
ТЕОРЕМА ТАНГЕНСОВ
Если 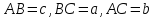 ,
,  , то
, то
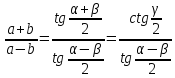
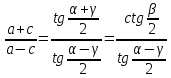
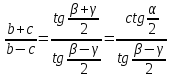
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Если 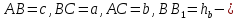 высота к стороне
высота к стороне 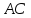 ,
, 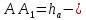 высота к стороне
высота к стороне 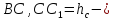 высота к стороне
высота к стороне  ,
, 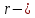 радиус вписанной окружности,
радиус вписанной окружности, 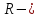 радиус описанной окружности,
радиус описанной окружности,  – полупериметр треугольника,
– полупериметр треугольника, 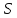 - площадь треугольника, то:
- площадь треугольника, то: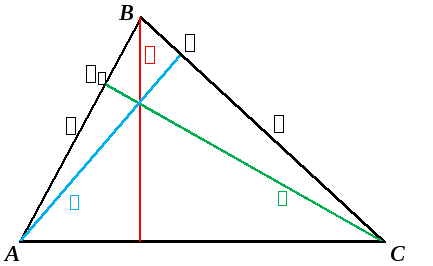
– формула Герона


СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
Средней линией треугольника называется отрезок, соединяющий середины двух сторон.
– средняя линия
ТЕОРЕМА: Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине:

Свойства средней линии треугольника.
Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия  .
.




Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника.


ПОДОБИЕ ТРЕУГОЛЬНИКОВ
Подобными называются треугольники, у которых углы равны, а соответствующие стороны пропорциональны. Соответствующие стороны – это стороны, которые лежат напротив равных углов.
Свойства подобных треугольников.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
 (из рисунка сверху)
(из рисунка сверху)
Отношение соответствующих линейных элементов (биссектрис, медиан, высот, серединных перпендикуляров и т.д.) равно коэффициенту подобия, т.е. в подобных треугольниках соответствующие линии пропорциональны.
Отношение периметров подобных треугольников равно коэффициенту подобия.
ПЕРВЫЙ ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ
ТЕОРЕМА: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
ВТОРОЙ ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ
ТЕОРЕМА: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
ТРЕТИЙ ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ
ТЕОРЕМА: Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
2







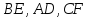 пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство:
пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство:
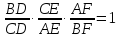
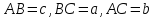 ,
, 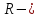 радиус описанной окружности, то
радиус описанной окружности, то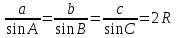

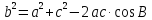
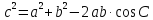
 , то
, то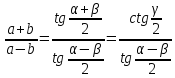
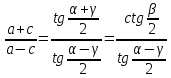
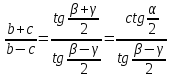
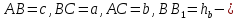 высота к стороне
высота к стороне 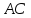 ,
, 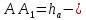 высота к стороне
высота к стороне 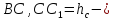 высота к стороне
высота к стороне  ,
, 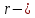 радиус вписанной окружности,
радиус вписанной окружности,  – полупериметр треугольника,
– полупериметр треугольника, 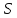 - площадь треугольника, то:
- площадь треугольника, то:


















