Вариант № 4
1. Найдите значение выражения 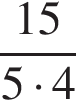
2. В таблице представлены нормативы по технике чтения в третьем классе.
| Отметка | Количество прочитанных слов в минуту |
| I и II четверти | III и IV четверти |
| «2» | 59 и менее | 69 и менее |
| «3» | 60−69 | 70−79 |
| «4» | 70−79 | 80−89 |
| «5» | 80 и более | 90 и более |
Какую отметку получит третьеклассник, прочитавший в феврале 65 слов за минуту?
В ответе укажите номер правильного варианта.
1) «2»
2) «3»
3) «4»
4) «5»
3. На координатной прямой отмечены числа 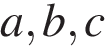 .
.
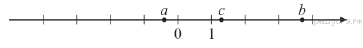
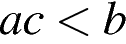
Какое из следующих утверждений неверно?
1) 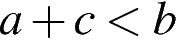
2) 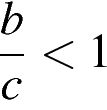
3) 
4) 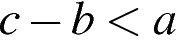
4. В каком случае числа расположены в порядке возрастания?
В ответе укажите номер правильного варианта.
1) 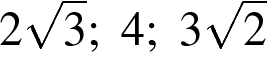
2) 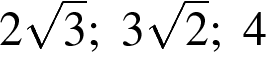
3) 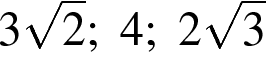
4) 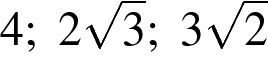
5. На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 9 августа. Ответ дайте в градусах Цельсия.
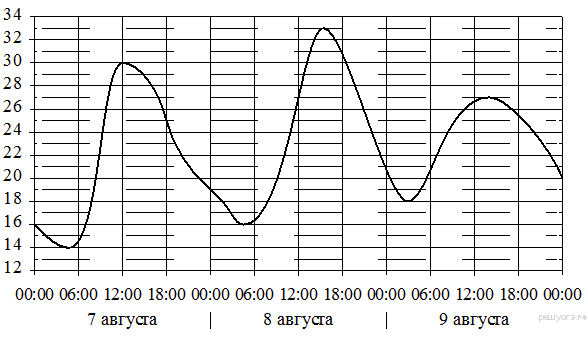
6. Найдите корни уравнения 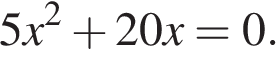
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. В начале 2010 г. в поселке было 730 жителей, а в начале 2011 г. их стало 803. На сколько процентов увеличилось число жителей поселка за год?
8.
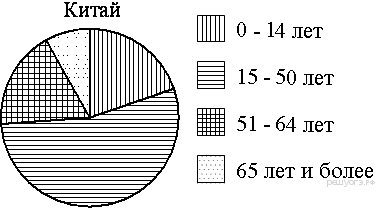 На диаграмме показан возрастной состав населения Китая.
На диаграмме показан возрастной состав населения Китая.
Сколько примерно людей младше 14 лет проживает в Китае, если население Китая составляет 1,3 млрд людей?
1) около 100 млн
2) около 260 млн
3) около 325 млн
4) около 150 млн
9. В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
10. На рисунках изображены графики функций вида 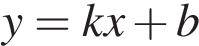 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов 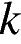 и
и 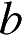 и графиками функций.
и графиками функций.
КОЭФФИЦИЕНТЫ
А) 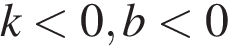
Б) 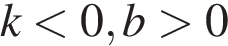
В) 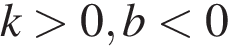
ГРАФИКИ
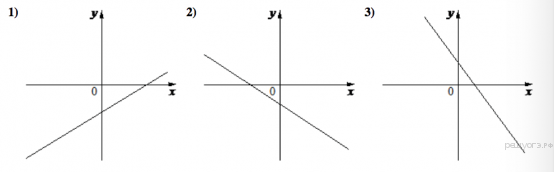
В таблице под каждой буквой укажите соответствующий номер.
11. Геометрическая прогрессия (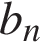 ) задана условиями:
) задана условиями: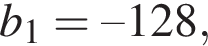
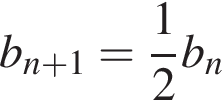 . Найдите
. Найдите 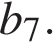
12. Найдите значение выражения при
13. Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
14. Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) x2 − 15
2) x2 + 15 0
3) x2 + 15
4) x2 − 15 0
15. На рисунке показано, как выглядит колесо с 7 спицами. Найдите величину угла (в градусах), который образуют две соседние спицы, если в колесе 45 спиц.
16.
В выпуклом четырехугольнике ABCD известно, что, , , . Найдите угол A. Ответ дайте в градусах.
17.
Центральный угол AOB, равный 60° , опирается на хорду АВ длиной 4. Найдите радиус окружности.
18.
Тангенс острого угла прямоугольной трапеции равен  Найдите её большее основание, если меньшее основание равно высоте и равно 58.
Найдите её большее основание, если меньшее основание равно высоте и равно 58.
19.
Найдите тангенс угла .
20. Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Если утверждений несколько, запишите их номера в порядке возрастания.
21. Сократите дробь
22. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько требуется свежих фруктов для приготовления 80 кг высушенных фруктов?
23. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
24. Каждое основание  и
и  трапеции
трапеции  продолжено в обе стороны. Биссектрисы внешних углов
продолжено в обе стороны. Биссектрисы внешних углов  и
и  этой трапеции пересекаются в точке
этой трапеции пересекаются в точке  , биссектрисы внешних углов
, биссектрисы внешних углов  и
и  пересекаются в точке
пересекаются в точке  . Найдите периметр трапеции
. Найдите периметр трапеции  , если длина отрезка
, если длина отрезка  равна 24.
равна 24.
25. Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
26. Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 54°, 62° и 64°.








 На диаграмме показан возрастной состав населения Китая.
На диаграмме показан возрастной состав населения Китая.










