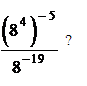Только до 31 августа! Материалы для учителей на каждый урок со скидкой до 45%

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 19.05.2025 19:30

Астахова Вера Григорьевна

учитель математики

58 лет

9 756

4 458

Подписчики

Подписки

Местоположение

Россия, Рубцовск

Специализация

Математика

Обо мне Блог Файлы Тесты Галерея Активность Награды

Тренировочный вариант по математике,№5 (ОГЭ)

Категория: Математика

05.01.2018 19:46

Тренировочный вариант №5 по математике в формате ОГЭ.

Просмотр содержимого документа
«Тренировочный вариант по математике,№5 (ОГЭ)»

Вариант №5

1. Найдите значение выражения 30−0,8⋅(− 10)².

2. В таблице приведены нормативы по бегу на 60 метров для учащихся 9 класса.

	Мальчики			Девочки
Отметка	«5»	«4»	«3»	«5»	«4»	«3»
Время (в секундах)	8,5	9,2	10,0	9,4	10,0	10,5

Какую отметку получит девочка, пробежавшая 60 метров за 9,52 секунды?

	1)	отметка «5»		2)	отметка «4»
	3)	отметка «3»		4)	норматив не выполнен

3. На координатной прямой отмечены числа x и y .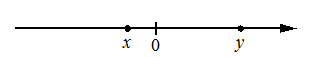

Какое из приведённых утверждений для этих чисел неверно?

y−x

x 2 y 0

x+y 0

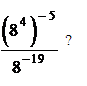
4. Какое из данных ниже чисел является значением выражения

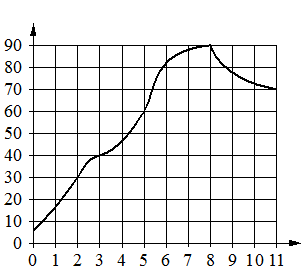
5. На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 30 °C до 40 °C.

6. Решите уравнение 10x²=80x.

Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

7. Спортивный магазин проводит акцию. Любой джемпер стоит 400 рублей. При покупке двух джемперов — скидка на второй джемпер 75%. Сколько рублей придётся заплатить за покупку двух джемперов в период действия акции?

8. На диаграммах показаны возрастные составы населения Китая, Индонезии, Японии и России. Определите по диаграммам, в какой из стран доля населения 0–14 лет наибольшая.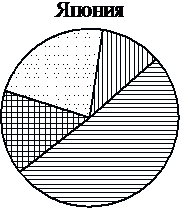

Китай

Индонезия

Япония

В ответе запишите номер выбранного варианта ответа.

9. В фирме такси в данный момент свободно 20 машин: 2 чёрных, 2 жёлтых
и 16 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

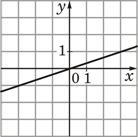
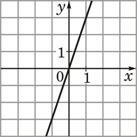
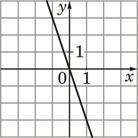
10. Установите соответствие между функциями и их графиками.

ФУНКЦИИ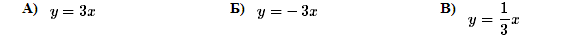

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

11. Выписаны первые три члена арифметической прогрессии: 20; 13; 6; …

Найдите 7-й член этой прогрессии.

12.

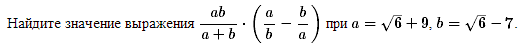
13. Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R,
где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите сопротивление R, если мощность составляет 150 Вт, а сила тока равна 5 А. Ответ дайте в омах.

14. Укажите решение системы неравенств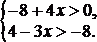

	1)	нет решений		2)
	3)			4)

15. Найдите угол, который минутная стрелка описывает за 2 минуты. Ответ дайте в градусах.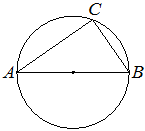

16. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.

17. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.

18. Синус острого угла треугольника равен . Найдите .

19. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.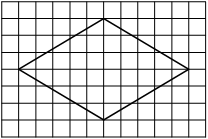

20. Какое из следующих утверждений верно?

	1)	В параллелограмме есть два равных угла.
	2)	Каждая из биссектрис равнобедренного треугольника является его медианой.
	3)	Площадь прямоугольного треугольника равна произведению длин его катетов.

В ответ запишите номер выбранного утверждения.

21. Решите систему уравнений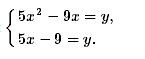

22. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

23. Постройте график функции y=|x|(x−1)−5x. Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

24. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=3, CK=19.

25. Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка L — середина стороны AB. Докажите, что DL — биссектриса угла ADC.

26. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.