Тренировочные задания к учебнику ФИЗИКА - 8.
Уроки 1 – 6. Тема «Тепловые явления».
Задание 1. Что происходит с молекулами при нагревании столбика спирта в термометре?
Решение. Температура характеризует среднюю скорость движения молекул вещества. Соответственно, при увеличении температуры молекулы, двигаясь в среднем быстрее, находятся в среднем на большем расстоянии друг от друга.
Ответ: увеличивается расстояние между молекулами.
Задание 2. Является ли примером броуновского движения беспорядочное движение цветочной пыльцы в капельке воды?
Решение. Броуновское движение — это беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием толчков со стороны молекул окружающей среды. Малыми частицами являются частички пыли цветов, их средой — капелька воды.
Ответ: да.
Задание 3. Как изменилась внутренняя энергия воды и пара после того как пар, имеющий температуру 120°С, впустили в воду при комнатной температуре?
Решение. Внутренняя энергия пропорциональна температуре тела и потенциальной энергии взаимодействия молекул тела между собой. После впускания горячего пара в холодную воду температура пара понизилась, а воды повысилась. Таким образом, внутренняя энергия пара уменьшилась, а воды увеличилась.
Ответ: внутренняя энергия пара уменьшилась, а воды увеличилась.
Задание 4. Какой(-ие) из видов теплопередачи осуществляется(-ются) без переноса вещества?
Ответ: без переноса вещества осуществляется теплопроводность и излучение.
Задание 5. В отсутствие теплопередачи объем газа увеличился. Как при этом изменились температура и внутренняя энергия газа?
Решение. В процессе без теплообмена при увеличении объёма температура уменьшается. Внутренняя энергия пропорциональна температуре тела и потенциальной энергии взаимодействия молекул тела между собой. Следовательно, температура и внутренняя энергия газа уменьшились.
Ответ: температура и внутренняя энергия газа уменьшились.
Задание 6. Турист разжёг костёр на привале в безветренную погоду. Находясь на некотором расстоянии от костра, турист ощущает тепло. Каким способом в основном происходит процесс передачи теплоты от костра к туристу?
Решение. Воздух плохо проводит тепло, поэтому посредством теплопередачи тепло в данном случае не передаётся. Явление конвекции заключается в том, что более тёплые слои воздуха поднимаются выше, а холодные опускаются вниз. Если ветра нет, то тёплые массы воздуха не достигают туриста, а поднимаются вверх. Поэтому в основном передача теплоты осуществляется путём излучения.
Ответ: излучением.
Задание 7. Какие изменения энергии происходят в куске льда при его таянии?
Решение. Внутренняя энергия тела — это суммарная кинетическая энергия движения молекул тела и потенциальная энергия их взаимодействия. При таянии лёд превращается в воду, поэтому увеличивается внутренняя энергия молекул воды, из которых состоит кусок льда.
Ответ: увеличивается внутренняя энергия воды, из которой состоит кусок льда
Задание 8. Какие из утверждений верны?
А. Диффузию нельзя наблюдать в твёрдых телах.
Б. Скорость диффузии не зависит от температуры вещества.
Решение. Диффузию можно наблюдать в твёрдых телах, например, слипание гладких свинцовых цилиндров. Скорость диффузии зависит от температуры вещества: как правило, чем выше температура ,тем скорость диффузии выше.
Ответ: оба утверждения неверны.
Задание 9. Мяч массой m бросают вертикально вверх со скоростью v с поверхности земли. От чего зависит внутренняя энергия мяча?
Решение. Внутренняя энергия пропорциональна температуре тела и потенциальной энергии взаимодействия молекул тела между собой. Таким образом, внутренняя энергия мяча зависит от массы и температуры мяча.
Ответ: от массы и температуры мяча
Уроки 7 – 9. Тема «Тепловые явления».
Задание 1. На рисунке 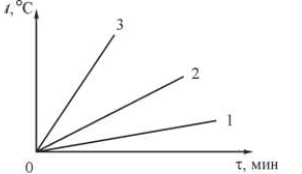 представлены графики зависимости температуры t от времени τ для трёх твёрдых тел одинаковой массы: из алюминия, из меди и из свинца. Тела нагревают на одинаковых горелках. Определите, какой график соответствует нагреванию тела из алюминия, какой — из меди, а какой — из свинца.
представлены графики зависимости температуры t от времени τ для трёх твёрдых тел одинаковой массы: из алюминия, из меди и из свинца. Тела нагревают на одинаковых горелках. Определите, какой график соответствует нагреванию тела из алюминия, какой — из меди, а какой — из свинца.
Решение. Количество теплоты Q, идущее на нагрев вещества равно mcΔt, где m — масса вещества, с — удельная теплоёмкость этого вещества, Δt — приращение температур.
Чтобы нагреть образцы одинаковой массы до одной температуры, нужно затратить разное количество тепла, пропорциональное их теплоёмкости. Поскольку горелки одинаковые, для передачи большего количества теплоты, нужно дольше нагревать образцы. Таким образом, чем больше теплоёмкость образца, тем меньший наклон на графике ему соответствует. Из табличных данных находим, что cсвинца меди алюм. Значит, график 1 — алюминий, график 2 — медь, график 3 — свинец.
Ответ: 1 — алюминий, 2 — медь, 3 — свинец
Задание 2. На рисунке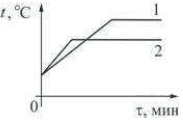 представлены графики нагревания и плавления двух твёрдых веществ — «1» и «2» — одинаковой массы, взятых при одинаковой начальной температуре. Образцы нагреваются на одинаковых горелках. Сравните удельные теплоёмкости этих двух веществ и температуры их плавления.
представлены графики нагревания и плавления двух твёрдых веществ — «1» и «2» — одинаковой массы, взятых при одинаковой начальной температуре. Образцы нагреваются на одинаковых горелках. Сравните удельные теплоёмкости этих двух веществ и температуры их плавления.
Решение.
Плавлению соответствуют участки графиков, параллельные оси времени, т. к. в это время полученная энергия идет не на нагрев, а на разрушение кристаллических связей. Чем выше располагается этот участок, тем выше температура плавления, в данном случае у вещества 1 она выше.
На нагревание вещества идёт количество теплоты: Q =cm(t2 – t1);
где m — масса вещества, с — удельная теплоёмкость этого вещества, Δt — приращение температур. Чтобы нагреть образцы до одной температуры, нужно затратить разное количество тепла, пропорциональное их удельной теплоёмкости. Поскольку горелки одинаковые, для передачи большего количества теплоты нужно дольше нагревать образцы. Первый образец греется дольше, поэтому вещество 1 обладает большей теплоёмкостью.
Ответ: У вещества «1» больше удельная теплоёмкость и температура плавления, чем у вещества «2».
Задание 3. Удельная теплоёмкость стали равна 500 Дж/кг·°С. Что это означает?
Решение. Удельная теплоемкость характеризует количество энергии, которое необходимо сообщить одному килограмму вещества для того, из которого состоит тело, для того, чтобы нагреть его на один градус Цельсия. Таким образом, для нагревания 1 кг стали на 1 °С необходимо затратить энергию 500 Дж.
Ответ: для нагревания 1 кг стали на 1 °С необходимо затратить энергию 500 Дж.
Задание 4. На рисунке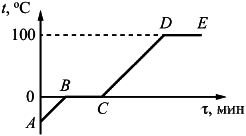 представлен график зависимости температуры от времени для процесса нагревания воды при нормальном атмосферном давлении. Первоначально вода находилась в твёрдом состоянии.
представлен график зависимости температуры от времени для процесса нагревания воды при нормальном атмосферном давлении. Первоначально вода находилась в твёрдом состоянии.
Какое из утверждений является неверным?
Решение. Неверным является утверждение под номером 3, поскольку процесс АВ — это нагревание. При нагревании внутренняя энергия тела увеличивается, поскольку средняя скорость движения молекул увеличивается.
Ответ В процессе АВ внутренняя энергия льда не изменяется.
Задание 5. На рисунке 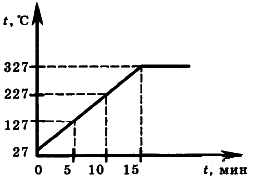 представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания? Удельную теплоёмкость свинца считать равной 130 Дж/кг∙°С
представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания? Удельную теплоёмкость свинца считать равной 130 Дж/кг∙°С
| Дано: m= 1 кг t = 10 мин. = 600c t2 – t1 = 200 C°. c =130 Дж/кг∙°С | Решение. Из графика находим, что за 10 минут свинец нагрелся на 200 C°. Вычислим количество теплоты, полученное свинцом: Q =cm(t2 – t1); Q = 1 кг 130 Дж/(кг∙°С)200∙°С = 26000Дж = 26 кДж Ответ: 26 кДж
|
| Q -? |
Задание 6. Какая из ложек нагреется быстрее при опускании в стакан с горячей водой деревянная или алюминиевая?
Решение. Алюминиевая ложка нагревается быстрее, так как теплопроводность алюминия выше.
Ответ: алюминиевая.
Задание 7. Удельная теплота плавления стали равна 78 кДж/кг. Что это означает?
Решение. По определению удельная теплота плавления — это количество теплоты, необходимое для того, чтобы перевести 1 кг вещества, взятого при температуре плавления, из твёрдого состояния в жидкое. Это означает, что для плавления 1 кг стали при температуре её плавления потребуется 78 кДж энергии.
Ответ: для плавления 1 кг стали при температуре её плавления потребуется 78 кДж энергии
Задание 8. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
| Дано: m0 = 4 кг t0 = 20 °C t1 = 83 °C. Cв =4200 Дж/кг∙°С | Решение. Плотность воды равна 1 кг/л, теплоемкость равна 4 200 Дж/кг. Таким образом, изначально мы имеем m0 = 4 кг воды при температуре t0 = 20 °C. Добавляется некоторое количество воды массой m1 при температуре t1 = 83 °C. Конечная температура смеси равна tкон, а её масса m0 + m1. Составим уравнение теплового баланса для процесса: Q =cв m 1(t1 – tкон ) — отданное в процессе тепло; Q =cв m 0(tкон – t0 ) — полученное в процессе тепло; cв m 1(t1 – tкон ) = cв m 0(tкон – t0. m1 = m0 (tкон – t0 ) / (t1 – tкон ); m1 = 4 кг ∙ ( 65 – 20) / ( 83 – 65) = 10 кг; следовательно, необходимо V = 10 л воды. Ответ: 10 л.
|
| V -? |
Задание 9. Три литра воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
| Дано: m1 = 3 кг t0 = 20 °C t1 = 100 °C. t = 40°C Cв =4200 Дж/кг∙°С | Решение. Составим уравнение теплового баланса для процесса: Qполученное = Qпереданное Получала тепло вода при температуре 20°С, отдавала — при 100 °С. Обозначим массу воды при 20 °С за m1, при 100 °С — за m2. Тогда Qполученное =cв m 1 ∙ (40 - 20 ); Вода отдала: Qпереданное =cв m 2 ∙ (100 -40 ); cв m 1∙ 20 = cв m 2∙ 60; m 2 = m 1 ∙ 20 / 60 = m1 ∙ 1/3; Учитывая, что плотность воды 1 кг/л, находим, что m1 = 3 кг, тогда m2 = 1 кг. Ответ: 1 кг.
|
| m2 -? |
Задание 10. Какое количество теплоты необходимо, чтобы нагреть 1 л воды от 20 °С до 100 °С? Вода нагревается в алюминиевой кастрюле массой 200 г. Тепловыми потерями пренебречь.
| Дано: m1 = 1 кг m2 = 200 г = 0,2 кг t0 = 20 °C t1 = 100 °C. Cв =4200 Дж/кг∙°С | Решение. В данном случае тепло получают кастрюля и вода. Для нагревания воды необходимо: Qводы =cв m 1(100 - 20 ); Для нагревания кастрюли: Qкастр =cал m 2(100 - 20 ); Qводы =cв m 1∙ 80 = 1 кг ∙ 4200 (Дж/кг °С) ∙ 80°С = 336 кДж; Qкастр = 0,2 кг ∙ 920 (Дж/кг °С) ∙ 80°С = 14,72 кДж; Таким образом: Q = Qводы+ Qкастр = 336 кДж + 14,72 кДж = 350,72 кДж, Ответ: 350,72 кДж. |
| Q -? |
Задание 11. При охлаждении стальной детали массой 100 г до температуры 32 С° выделилось 5 кДж энергии. Какова была температура стали до охлаждения?
| Дано: m= 100г = 0,1 кг t2 = 32 C°. сст =500 Дж/(кг∙°С) Q = 5000 Дж | Решение. Количество теплоты, выделяющееся при охлаждении стали: Q =с cт m (t1 – t2); где cст — удельная теплоёмкость стали, m — масса стали, t1 и t2 — температура стали до и после охлаждения соответственно. Выразим t1: (t1 – t2)= Q / (с cт m); t1= Q / (с cт m) + t2; t1=5000 Дж / (500 Дж/(кг∙°С) ∙ 0,1 кг) + 32 C° = 132∙°С; Ответ: 132∙°С
|
| t1-? |
Задание 12. При нагревании куска металла массой 200 г от 20 °С до 60 °С его внутренняя энергия увеличилась на 2400 Дж. Какова удельная теплоёмкость металла?
| Дано: m= 0,2 кг t1 = 20 C°. t2 = 60C°. Q = 2400 Дж
| Решение. Удельная теплоёмкость металла — это количество теплоты, которое необходимо сообщить одному килограмму металла для того, чтобы он нагрелся на 1 C°. Изменение внутренней энергии обозначим через Q. Вычислим удельную теплоёмкость данного металла из: Q =c m (t2 – t1); С = Q / (m (t2 – t1); С = 2400 Дж / 0,2 кг∙(60 – 20) C° = 300 Дж/(кг∙°С); Ответ: 300 Дж/(кг∙°С).
|
| c -? |
Уроки 1 – 7. Тема «Изменение агрегатных состояний вещества»
Задание 1. На рисунке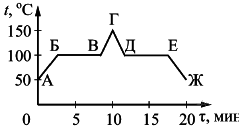 приведён график зависимости температуры t воды от времени τ при нормальном атмосферном давлении.
приведён график зависимости температуры t воды от времени τ при нормальном атмосферном давлении.
Какое из утверждений является неверным?
1) Участок АБ соответствует процессу нагревания воды.
2) В процессе, соответствующем участку ЕЖ, внутренняя энергия воды уменьшается.
3) Точка Е соответствует твёрдому состоянию воды.
4) В процессе, соответствующем участку БВ, внутренняя энергия системы вода-пар увеличивается.
Решение. Проанализируем утверждения.
1) Утверждение верно: участок АБ соответствует процессу нагревания воды.
2) Внутренняя энергия тела пропорциональна средней скорости движения молекул и энергии потенциального взаимодействия между ними. При охлаждении средняя скорость движения молекул уменьшается, следовательно, утверждение верно.
3) Поскольку вода при атмосферном давлении кипит при 100 °C, точка Е не может соответствовать твёрдому состоянию воды.
4) На участке БВ системе сообщается энергия, которая идёт на испарение воды. Молекулы пара двигаются в среднем быстрее молекул воды. Следовательно, внутренняя энергия системы увеличивается.
Ответ: 3.
Задание 2. На рисунке приведен график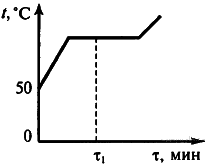 зависимости температуры воды от времени. Начальная температура воды 50 °С. В каком состоянии находится вода в момент времени τ1?
зависимости температуры воды от времени. Начальная температура воды 50 °С. В каком состоянии находится вода в момент времени τ1?
Решение. Горизонтальный участок на графике соответствует 100 °C, следовательно, В момент времени τ1 происходило парообразование воды и часть воды находилась в жидком состоянии, часть — в газообразном.
Ответ: часть воды — в жидком состоянии и часть воды — в газообразном.
Задание 3. На рисунке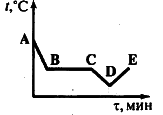 приведен график зависимости температуры спирта от времени при его охлаждении и последующем нагревании. Первоначально спирт находился в газообразном состоянии. Какой участок графика соответствует процессу конденсации спирта?
приведен график зависимости температуры спирта от времени при его охлаждении и последующем нагревании. Первоначально спирт находился в газообразном состоянии. Какой участок графика соответствует процессу конденсации спирта?
Решение. Процессу конденсации соответствует горизонтальный участок графика. Поскольку изначально спирт находился в газообразном состоянии, процессу конденсации спирта соответствует участок ВС.
Ответ: ВС
Задание 4. Испарение и кипение — два процесса перехода вещества из одного агрегатного состояния в другое. Общей характеристикой этих процессов является то, что они
А. представляют собой процесс перехода вещества из жидкого состояния в газообразное.
Б. происходят при определённой температуре.
Какое (ие) из данных утверждений являются правильными?
Решение. Испарение — процесс перехода вещества из жидкого состояние в газообразное. Кипение — процесс интенсивного парообразования, происходящий как со свободной поверхности жидкости, так и внутри неё. Испарение происходит при любой температуре, а кипение — только при температуре кипения.
Ответ: только А.
Задание 5. Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении?
| Дано: mп = 2 кг t0 = 100 °C t1 = 40 °C. Cв =4200 Дж/кг∙°С λп = 2300 кДж / кг | Решение. В данном случае тепло отдавали пар и вода. Пар отдал: Qпара =λ m п; Qпара = 2 кг ∙2300 кДж / кг = 4600 кДж; вода отдала: Qводы =cв m п(100 - 40); Qводы =cв m п∙ 60 = 2 кг ∙ 4200 (Дж/кг °С) ∙ 60°С = 504 кДж; Таким образом: Q = Qводы+ Qпара = 4600 кДж + 504кДж = 5104кДж,
Ответ: 5104 кДж. |
| Q -? |
Задание 6. Сколько спирта надо сжечь, чтобы нагреть воду массой 2 кг на 29° С? Считать, что вся энергия, выделенная при сгорании спирта, идёт на нагревание воды.
| Дано: m1 = 2 кг t0 - t1 = 29 °C q = 2,9 ∙ 107 Дж/кг Cв =4200 Дж/кг∙°С | Решение. Составим уравнение теплового баланса для процесса: Qполученное = Qпереданное Получала тепло вода, отдавал —спирт. Обозначим массу воды за m1, спирта — за m2. Тогда Qполученное =cв m 1 ∙ 29 °С; Спирт отдал: Qпереданное = q ∙m 2; Из уравнения теплового баланса находим, что: cв m 1∙ 29 = q m 2; m 2 = cв m 1∙ 29 / q = 4200 Дж/кг∙°С∙2 кг∙29°C / 2,9 ∙ 107 Дж/кг = 8.4 ∙ 10-3кг = 8,4 г; Ответ: 8.4 г.
|
| m2 -? |
Задание 7. В стакан, содержащий лед при температуре −5 °С, налили воду, имеющую температуру 40 °С. Каково отношение массы воды к массе льда, если весь лед растаял и в стакане установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь.
| Дано: t0 - t1 = 5 °C t2 – t0 = 40 °C λ = 330 кДж/кг Cв =4200 Дж/кг∙°С cл = 2,1 кДж/кг∙°С | Решение. Составим уравнение теплового баланса для процесса: Qполученное = Qпереданное Получал тепло лёд в процессе нагревания и плавления, отдавала — вода. Обозначим массу воды за m1, льда — за m2. Тогда Qполученное =Qнагрев+ Qплав = cл m 2 ∙ ( 0 –(- 5) °С) + m 2λ = m 2 (cл∙ 5°С + λ); Вода отдала: Qпереданное = св ∙m 1(40 – 0) °С Из уравнения теплового баланса находим, что: m 1 / m 2 = (cл∙ 5°С + λ)/ = св ∙40 °С = (2,1 кДж/кг∙°С∙5°С +330 кДж/кг) / 4,2 кДж/кг∙°С∙40 °С = 340,5 кДж/кг / 168 кДж/кг = 2,02; Ответ: 2,02.
|
| m2 -? |
Задание 8. Какое количество теплоты выделится при кристаллизации воды массой 1 кг, взятой при температуре 10 °С?
| Дано: m = 1 кг t0 = 10 °C t1 = 0 °C. λ = 330 кДж/кг Cв =4200 Дж/кг∙°С | Решение. Сначала вода охлаждается до температуры кристаллизации — 0 °C; при этом выделяется: Qохл =cв m ∙ (10 – 0) °С; Qохл =4200 Дж/кг∙°С∙1 кг ∙ 10 °C = 42 кДж; потом кристаллизуется; при этом выделяется: Qкрист = λ ∙m ; Qкрист =330 кДж/кг∙1 кг = 330 кДж. Таким образом, Q = Qкрист + Qохл =42 кДж + 330 кДж. = 372 кДж. Ответ: 372 кДж
|
| Q -? |
Уроки 8 – 13. Тема «Изменение агрегатных состояний вещества».
Задание 1. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
| Дано: А1 = 23 106 Дж m = 2 кг q = 4,6 ∙ 107 Дж/кг
| Решение. КПД есть отношение полезной работы A1 к полной совершённой работе A2. Полной работой является энергия, которая выделилась при сжигании 2 кг бензина. Тогда КПД равен: η = А1 / А2 = А1 / (m∙ q); η = 23 106 Дж / (2 кг∙4,6 ∙ 107 Дж/кг) = 0,25 = 25%. Ответ: 25%. |
| η -? |
Задание 2. Автомобиль УАЗ израсходовал 30 кг бензина за 2 ч. езды. Чему равна мощность двигателя автомобиля, если его КПД составляет 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
| Дано: η = 30% = 0,3 m= 30 кг q = 4,6 ∙ 107 Дж/кг t = 2 ч =2 ∙ 3600 с
| Решение. КПД определяется как отношение полезной работы к энергии, потребляемой двигателем η = A/Q. Мощность двигателя — это отношение полезной работы совершаемой двигателем ко времени: N = A/t. Энергия, полученная двигателем от 30 кг бензина Q = m q; Q = 30 кг∙4,6 ∙ 107 Дж/кг = 1,38 ∙ 109Дж. Работу А выразим из первой формулы и подставим в N = A/t = Q∙η / t; подставим цифры: N = 1,38 ∙ 109Дж∙0,3 / 2 ∙ 3600 с = 0,00575∙107Вт = 57,5 кВт Ответ: 57,5 кВт |
| η -? |
Задание 3. Найдите массу бензина, израсходованную автомобилем УАЗ за 3 ч. езды, если мощность его двигателя равна 57,5 кВт, а его КПД 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
| Дано: η = 30% = 0,3 N = 57,5 кВт = 57500 Вт q = 4,6 ∙ 107 Дж/кг t = 3 ч = 3 ∙ 3600 с
| Решение. КПД определяется как отношение полезной работы к энергии, потребляемой двигателем η = A/Q. Мощность двигателя — это отношение полезной работы совершаемой двигателем ко времени: N = A/t. Энергия, полученная двигателем от сжигания 30 кг бензина Q = m q; A=N∙t; тогда m = Q / q = N ∙ t / η ∙ q; m = 57500 Вт ∙ 3 ∙ 3600 с/0,3 ∙ 4,6 ∙ 107 Дж/кг = 45 г.
Ответ: 45 г.
|
| m -? |
Задание 4. Сколько граммов воды можно нагреть на спиртовке на 30 °С, если сжечь в ней 21 грамм спирта? КПД спиртовки (с учётом потерь теплоты) равен 30%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
| Дано: η = 30% = 0,3 q = 2,9 ∙ 107 Дж/кг Cв =4200 Дж/кг∙°С Δ t = 30 °С m сгор = 21 г = 0,021кг
| Решение. При нагревании тела на температуру 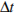 тело получает количество теплоты: Q =c m Δ t; тело получает количество теплоты: Q =c m Δ t; При сгорании тела выделяется энергия Qсгор = m сгор q. Учитывая, что КПД спиртовки равен 30%, получаем: Q = 0,3 Qсгор, тогда c m Δ t = 0,3 m сгор q.и m =0,3 m сгор q / c Δ t m = 0,3∙2,9 ∙ 107 Дж/кг∙0,021кг / 4200 Дж/кг∙°С∙30 °С = 1450 г. Ответ: 1450 г.
|
| m -? |
Задание 5. Определите энергию, необходимую для превращения в пар 1 кг спирта при температуре его кипения. Сколько энергии выделится при его конденсации при этой температуре? (Удельная теплота парообразования спирта 0,9·106 Дж/кг).
Решение. Удельная теплота парообразования показывает, сколько энергии необходимо для превращения в пар 1 кг вещества при температуре его кипения или сколько энергии выделится при его конденсации при этой температуре. Следовательно, для превращения в пар 1 кг спирта необходимо 0,9·106 Дж энергии. При конденсации спирта выделится столько же энергии, 0,9·106 Дж.
Ответ: 0,9·106 Дж
Уроки 8 – 13. Тема «Электрические явления».
Задание 1. Положительно заряженная стеклянная палочка притягивает подвешенный на нити лёгкий шарик из алюминиевой фольги. Может ли заряд шарика быть отрицательным либо равным нулю?
Решение. Заряд шарика может быть как отрицательным, так и равен нулю. В последнем случае возникает индуцированный (наведённый) заряд, т. к. алюминий является проводником.
Ответ: да.
Задание 2 Ученик положил металлическую линейку на выключенную электрическую лампочку, поднес к её концу, не касаясь, отрицательно заряженную палочку и начал осторожно перемещать палочку по дуге окружности. 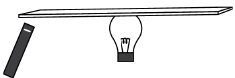 Линейка при этом поворачивалась вслед за палочкой. Почему?
Линейка при этом поворачивалась вслед за палочкой. Почему?
Решение. 1) Предположим, что между палочкой и линейкой действует сила гравитационного тяготения. Но сила тяготения прямо пропорциональна гравитационной постоянной и произведению масс. Гравитационная постоянная имеет порядок 10-11 кг, а массы линейки и палочки порядок 10-3 кг, следовательно, её явно недостаточно для того, чтобы повернуть линейку.
2) Предположим, на ближайшем к палочке конце линейки образуется избыточный отрицательный заряд, и она притягивается к линейке. Тогда линейка бы не вращалась, а вся перемещалась бы к палочке.
3) Предположим, на ближайшем к палочке конце линейки образуется избыточный положительный заряд, и она притягивается к линейке. Поскольку палочка заряжена отрицательно, частицы, имеющие отрицательный заряд в линейке стремятся удалиться от палочки, таким образом, на ближайшем к палочке конце линейки образуется избыточный положительный заряд, и она притягивается к линейке.
Ответ: на ближайшем к палочке конце линейки образуется избыточный положительный заряд, и она притягивается к линейке.
Задание 3. К одному из незаряженных электрометров, 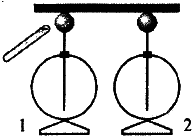 соединенных проводником, поднесли отрицательно заряженную палочку. Как распределится заряд на электрометрах?
соединенных проводником, поднесли отрицательно заряженную палочку. Как распределится заряд на электрометрах?
Решение. Заметим, что палочку подносят, но не касаются ею электрометра, поскольку палочка заряжена отрицательно, то она притягивает положительные заряды, на электрометре 1 образуется избыточный положительный заряд. При этом будет создан недостаток положительных зарядов на втором электрометре, или, что то же самое, избыток отрицательного заряда.
Ответ: на электрометре 1 будет избыточный положительный заряд, на электрометре 2 — избыточный отрицательный заряд
Задание 4. В вершинах равностороннего треугольника (см. рисунок) 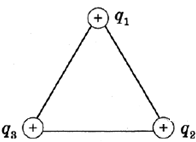 расположены заряды q1 = q, q2 = 2q и q3 = 3q .Для каких зарядов сила электрического взаимодействия, действующая между ними, максимальна?
расположены заряды q1 = q, q2 = 2q и q3 = 3q .Для каких зарядов сила электрического взаимодействия, действующая между ними, максимальна?
Решение. Сила электрического взаимодействия зависит от величины зарядов: чем больше заряды, тем больше сила., действующая между ними. Поэтому сила будет максимальна для зарядов q3 и q2, поскольку они имеют максимальный по модулю заряд.
Ответ: для зарядов q3 и q2.
Задание 5. В вершинах равностороннего треугольника (см. рисунок)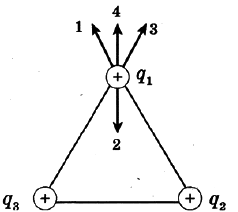 расположены равные по модулю заряды q1, q2 и q3. Какому вектору сонаправлена суммарная сила, действующая на заряд q1 со стороны зарядов q2 и q3?
расположены равные по модулю заряды q1, q2 и q3. Какому вектору сонаправлена суммарная сила, действующая на заряд q1 со стороны зарядов q2 и q3?
Решение. Сила электрического взаимодействия между первым и вторым шаром направлена по направлению 1, между первым и третьим — по направлению 3. Равнодействующая этих сил, равная их векторной сумме, будет направлена по направлению 4.
Ответ: вектору 4.
Задание 6. Два маленьких шарика — А и В — удерживают (см. рисунок) в равновесии. 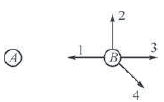 Оба шарика заряжены положительно. Какой из векторов, изображённых на рисунке, правильно указывает направление электрической силы, действующей на шарик В со стороны шарика A?
Оба шарика заряжены положительно. Какой из векторов, изображённых на рисунке, правильно указывает направление электрической силы, действующей на шарик В со стороны шарика A?
Решение. По закону Кулона на одноимённо заряженные шарики действует сила отталкивания вдоль прямой, соединяющей заряды.
Ответ: 3.
Задание 7. Из какого материала может быть сделан стержень (см. рис.),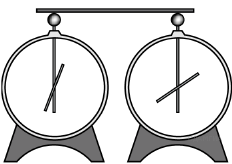 соединяющий электроскопы?
соединяющий электроскопы?
А. Сталь
Б. Стекло
Решение. Материал, из которого изготовлен стержень, явно не является проводником, поскольку в этом случае стрелки электрометров бы отклонились на одинаковый угол. Так как стекло является диэлектриком, стержень может быть только стеклянным.
Ответ: только Б.
Задание 8. В течение 600 с через потребитель электрического тока проходит заряд 12 Кл. Чему равна сила тока в потребителе?
Решение. Сила тока равна заряду, протекающему через поперечное сечение проводника за единицу времени, поэтому сила тока равна 12 Кл : 600 с = 0,02 А.
Ответ: 0,02 А
Задание 9. По проводнику течет ток 8 А. Какой электрический заряд проходит через поперечное сечение проводника за 40 с?
Решение. Сила тока есть заряд, проходящий через поперечное сечение проводника за единицу времени, поэтому в условиях задачи через поперечное сечение проводника за единицу времени, пройдёт заряд, равный 8 А · 40 с = 320 Кл.
Ответ: 320 Кл
Уроки 14 – 18. Тема «Электрические явления».
Задание 1.
Имеется три резистора (см. рисунок)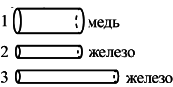 , изготовленных из различных материалов и имеющих различные размеры Наименьшее электрическое сопротивление имеет(-ют)
, изготовленных из различных материалов и имеющих различные размеры Наименьшее электрическое сопротивление имеет(-ют)
Решение. Сопротивление проводника опреде
R = ρ·L / S
где ρ — удельное сопротивление проводника, зависящее от материала, из которого изготовлен проводник, l — длина проводника, S — площадь сечения.
Удельное сопротивление меди меньше, чем железа. Кроме того, из рисунка видно, что площадь сечения первого проводника наибольшая.
Ответ: резистор 1.
Задание 2. Электрическая цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединённых последовательно. Лампочка станет гореть ярче, если
1) подсоединить к проволоке последовательно вторую такую же проволоку
2) железную проволоку заменить на нихромовую
3) поменять местами проволоку и лампочку
4) подсоединить к проволоке параллельно вторую такую же проволоку
Решение. Проанализируем все утверждения.
1) Если подсоединить к проволоке последовательно вторую такую же проволоку, то сопротивление цепи увеличится, поскольку оно прямо пропорционально длине проводника. Следовательно, сила тока в цепи уменьшаться и лампочка станет гореть тусклее.
2) Удельное сопротивление нихрома больше чем железа, следовательно, лампочка будет гореть тусклее.
3) При последовательном соединении сила тока в цепи одинакова на каждом участке, поэтому при перестановке любых элементов местами, яркость лампочки не измениться.
4) При параллельном соединении двух резисторов общее сопротивление участка вычисляется по формуле:
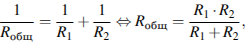
где R1 — сопротивление первого резистора, R2 — сопротивление второго резистора. Поскольку подсоединили точно такую же проволоку, R1 = R2 = R, тогда Rобщ = 0,5R. Так как сопротивление уменьшилось, ток в цепи увеличился, следовательно, лампочка станет гореть ярче.
Ответ:4.
Задание 3. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединённых последовательно. Лампочка станет гореть ярче, если
1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую
Решение. Проанализируем все утверждения.
1) Сопротивление проводника обратно пропорционально площади его сечения, следовательно, при замене проволоки на более тонкую, сопротивление цепи увеличиться, лампочка будет гореть тусклее.
2) Сопротивление проводника прямо пропорционально его длине. Следовательно, если уменьшить длину проволоки, лампочка будет гореть ярче.
3) При последовательном соединении сила тока в цепи одинакова на каждом участке, поэтому при перестановке любых элементов местами, яркость лампочки не изменится.
4) Удельное сопротивление нихрома больше чем железа, следовательно, лампочка будет гореть тусклее.
Ответ: 2.
Задание 4. Три резистора, сопротивления которых: R1 = 3 Ом; R2 = 6 Ом и R3 = 9 Ом, соединены последовательно. Вольтметр, подключённый параллельно второму резистору, показывает напряжение 12 В. Чему равно напряжение на всем участке цепи? Вольтметр считать идеальным.
| Дано: R1 = 3 Ом R2 = 6 Ом R3 = 9 Ом U2 = 12 B
| Решение. По закону Ома сила тока, протекающего через второй резистор I2 = U/R = 12 B/6 OM = 2 A. Поскольку соединение последовательное, сила тока на первом и третьем резисторе такая же. Вычислим напряжение на первомU1 = 3 Ом · 2 А = 6 В и третьем U3 = 9 Ом · 2 А = 18 В. Поскольку соединение последовательное напряжение на всём участке цепи U = 12 + 18 + 6 = 36 В. Ответ: 36 B.
|
| U -? |
Задание 5.Два алюминиевых проводника одинаковой длины имеют разную площадь поперечного сечения: площадь поперечного сечения первого проводника 0,5 мм, а второго проводника 4 мм2. Сопротивление какого из проводников больше и во сколько раз?
Решение. Сопротивление проводника вычисляется по формуле R = ρ · L/S
Где ρ— удельное сопротивление проводника, L — длина проводника, S — площадь сечения. Следовательно, сопротивление второго проводника меньше сопротивления первого в 4 мм2 / 0,5 мм2 = 8 раз.
Ответ: сопротивление первого проводника в 8 раз больше, чем второго.
Задание 6.В таблице представлены результаты исследования зависимости силы тока от напряжения на концах резистора. Какое значение напряжения должно стоять в пустой клетке?
Решение. Из первого столбца найдём сопротивление резистора: 8 В : 2 А = 4 Ом. Следовательно, в пустой клетке должно стоять значение напряжения 4 Ом · 4 А = 16 В.
Ответ: 16 В.
Задание 7. Что показывает амперметр A в цепи, 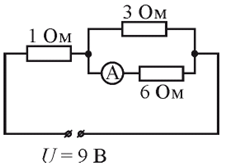 схема которой приведена на рисунке?
схема которой приведена на рисунке?
| Дано: R1 = 1 Ом R2 = 3 Ом R3 = 6 Ом U = 9 B | Решение. Амперметр показывает силу тока, проходящего через резистор сопротивлением в 6 Ом. Рассчитаем суммарное сопротивление цепи: Rобщ = 1 + 1: (1/3 + 1/6) = 1+2 = 3 Ом, т. к. R2 и R3 соединены параллельно. Ток, протекающий через резистор R1 равен сумме токов, протекающих через резисторы R2 и R3. Напряжение U складывается из напряжения на левом резисторе R1 и напряжения на параллельном участке сопротивлением R2 · R3/ (R2 + R3). U = I1 · R1+ I1 R2 · R3/ (R2 + R3). Следовательно, I1 = U: ( R1+ R2 · R3/ (R2 + R3). I1 = 9 : (1+ 3·6/(3+6) = 3 А. Напряжение, прикладываемое к параллельному участку: Uпарал = U - I1 · R1 = 9 – 3· 1 = 6 В. Найдём ток, протекающий через R2: I2 = Uпара / R2 = 6 / 6 = 1 A. Ответ: 1 A.
|
| I2 -? |
Уроки 19 – 20. Тема «Электрические явления».
Задание 1. Алюминиевая, железная и нихромовая проволоки, имеющие одинаковые размеры, соединены последовательно и подключены к источнику тока. На какой из проволок при прохождении электрического тока будет выделяться наибольшее количество теплоты за одно и то же время?
Решение. По закону Джоуля-Ленца количество теплоты, выделяемое проводником прямо пропорционально сопротивлению проводника. Сопротивление проводника вычисляется по формуле R = ρ · L/Sгде ρ — удельное сопротивление проводника, l — длина проводника, S — площадь сечения. Удельное сопротивление нихрома наибольшее, следовательно, на нихромовой проволоке выделиться наибольшее количество тепла.
Ответ: на нихромовой.
Задание 2. В электрической цепи (см. рисунок)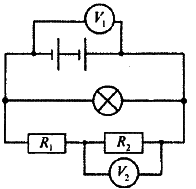 вольтметр V1 показывает напряжение 2 В, вольтметр V2 — напряжение 0,5 В. Чему равно напряжение на лампе?
вольтметр V1 показывает напряжение 2 В, вольтметр V2 — напряжение 0,5 В. Чему равно напряжение на лампе?
Решение. Лампа и первый вольтметр соединены параллельно. Следовательно, напряжение на них одинаково.
Ответ: 2,0 В.
Задание 3. К источнику постоянного тока (см. рисунок),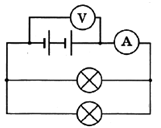 подсоединили две лампы, имеющие одинаковые электрические сопротивления. Чему равна мощность электрического тока, потребляемая каждой лампой, если показания идеального амперметра и вольтметра равны соответственно 3 А и 6 В ?
подсоединили две лампы, имеющие одинаковые электрические сопротивления. Чему равна мощность электрического тока, потребляемая каждой лампой, если показания идеального амперметра и вольтметра равны соответственно 3 А и 6 В ?
| Дано: I = 3 A U = 6 B
| Решение. Лампы соединены параллельно. Вычислим общее сопротивление участка цепи, на котором расположены обе лампы: 1/R = 1/r + 1/r; следовательно, R = r/2. где R — общее сопротивление участка цепи, на котором расположены обе лампы, включённые в цепь, изображённую на рисунке, r — сопротивление лампы. Из закона Ома находим, что R = 6 В/3 А = 2 Ом. Следовательно, сопротивление лампы равно 4 Ом. Мощность лампы. P = U·I = U2 / R; P = 36 B2/ 4 Ом = 9 Bт. Ответ: 9Вт.
|
| P -? |
Задание 4. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если R1 = 6 Ом, R2 = 2 Ом, R3 = 2 Ом?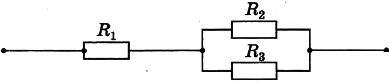
| Дано: R1 = 6 Ом, R2 = 2 Ом, R3 = 2 Ом
| Решение. Поскольку R2 = R3 = 2 Ом, сопротивление параллельного участка 1/R23 = 1/R + 1/R = 2/R; R23 = 2/2 = 1 Ом. Это сопротивление последовательно соединено с R23. Общее сопротивление последовательно соединённого участка есть сумма входящих в него сопротивлений: R = 6 + 1 = 7 Ом.
Ответ: 7 Ом.
|
| R23 -? |
Задание 5. На рисунке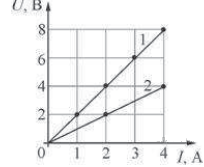 показаны два графика зависимости напряжения U на концах двух проводников — «1» и «2» — от силы тока I в них. Эти проводники соединили последовательно. Чему равно общее сопротивление проводников?
показаны два графика зависимости напряжения U на концах двух проводников — «1» и «2» — от силы тока I в них. Эти проводники соединили последовательно. Чему равно общее сопротивление проводников?
Решение. При последовательном соединении сопротивления суммируются. Из закона Ома U = I·R, откуда находим сопротивления первого и второго проводников:
R1 = 8 B: 4A = 2 OM; R2 = 4B : 4A =1 OM.
Тогда общее сопротивление проводников R = 3 Ом.
Ответ: 3 Ом.
Задание 6. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
| А) работа тока Б) сила тока B) мощность тока | 1) q/t 2) q·U 3) RS/L 4) U·I 5) U/I |
Решение. Сопоставим физическим величинам формулы.
А) Работа тока вычисляется по формуле 2.
Б) Сила тока вычисляется по формуле 1.
В) Мощность тока вычисляется по формуле 4.
Ответ: А – 2, Б – 1, В – 4.
Задание 7. Установите соответствие между научными открытиями и именами учёных, которым эти открытия принадлежат. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ОТКРЫТИЯ | ИМЕНА УЧЕНЫХ |
| А) экспериментальное открытие магнитного действия электрического тока Б) экспериментальное открытие явления электромагнитной индукции B) экспериментальное открытие электромагнитных волн | 1) А. С. Попов 2) Х. К. Эрстед 3) Г. Герц 4) Дж. Максвелл 5) М. Фарадей |
Решение. A) Экспериментальное открытие магнитного действия электрического тока в 1820 году осуществил Х. К. Эрстед.
Б) Экспериментальное открытие явления электромагнитной индукции сделал в 1831 году М. Фарадей.
B) Экспериментальное открытие электромагнитных волн осуществил Г. Герц.
Ответ: А - 2, Б – 5, В – 3.
Уроки 1– 5. Тема «Электромагнитные явления».
Задание 1.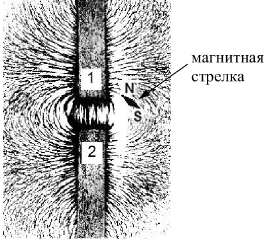 На рисунке представлена картина линий магнитного поля от двух полосовых магнитов, полученная с помощью железных опилок. Каким полюсам полосовых магнитов, судя по расположению магнитной стрелки, соответствуют области 1 и 2?
На рисунке представлена картина линий магнитного поля от двух полосовых магнитов, полученная с помощью железных опилок. Каким полюсам полосовых магнитов, судя по расположению магнитной стрелки, соответствуют области 1 и 2?
Решение. Поскольку магнитные линии замкнуты, полюса не могут быть одновременно южными или северными. Буква N (North) обозначает северный полюс, S (South) — южный. Северный полюс притягивается к южному. Следовательно, область 1 — южный полюс, область 2 — северный полюс.
Ответ: 1 — южному; 2 — северному полюсу.
Задание 2. Ток силой I протекает по прямолинейному участку провода (см. рисунок); 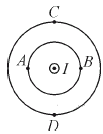 (ток направлен «на нас»). В какой точке вектор индукции магнитного поля, создаваемого током, направлен влево (в плоскости рисунка)?
(ток направлен «на нас»). В какой точке вектор индукции магнитного поля, создаваемого током, направлен влево (в плоскости рисунка)?
Решение. Направление вектора магнитной индукции для провода определяется правилом правой руки или правилом правого буравчика (буравчик выкручивается), следовательно, вектор индукции магнитного поля направлен влево в точке C.
Ответ: в точке С.
Уроки 1– 5. Тема «Световые явления».
Задание 1 Луч света падает на плоское зеркало. Угол между падающим лучом и отражённым увеличили на 20°. Как изменился угол между зеркалом и отражённым лучом
Решение. Угол падения равен углу отражения. При этом угол между зеркалом и отражённым лучом уменьшился на 10°.
Ответ: уменьшился на 10°
Задание 2. На рисунке 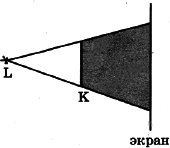 изображены точечный источник света L, предмет K и экран, на котором получают тень от предмета. Как изменятся размеры тени о мере удаления предмета от источника света и приближения его к экрану?
изображены точечный источник света L, предмет K и экран, на котором получают тень от предмета. Как изменятся размеры тени о мере удаления предмета от источника света и приближения его к экрану?
Решение. По мере удаления предмета от источника света и приближения его к экрану размеры тени будут уменьшаться (можно построить). Границы тени не будут ни размываться, ни становиться более чёткими.
Ответ: размеры тени будут уменьшаться.
Задание 3. Предмет ABCD отражается в плоском зеркале. Изображение A1B1C1D1 этого предмета в зеркале правильно показано на рисунке
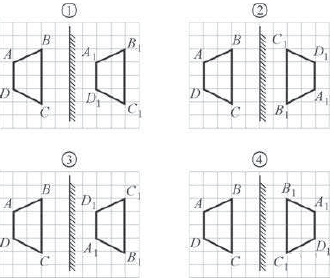
Решение. В плоском зеркале пересекаются все лучи испытывают только отражение без преломления, а продолжения лучей пересекаются симметрично относительно самих лучей, поэтому изображение получается прямое и повёрнутое в противоположную сторону.
Ответ: на 4.
Задание 4. На рисунке изображены оптическая ось ОО1 тонкой линзы, предмет А и его изображение А1, а также ход двух лучей, участвующих в формировании изображения.
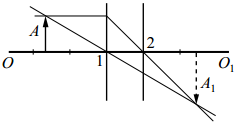
Согласно рисунку, в какой его точке находится фокус линзы?
Решение. Поскольку параллельный главной оптической оси луч после преломления прошёл через точку 2 на оптической оси, фокус расположен в точке 2. Причём линза является собирающей, поскольку луч отклонился в сторону главной оптической оси.
Ответ: в точке 2.
Задание 5. Каким бывает изображение предмета в рассеивающей линзе?
Решение. По построению изображение предмета в рассеивающей линзе всегда мнимое и уменьшенное.
Ответ: всегда мнимое и уменьшенное.
Задание 6.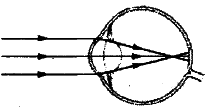 На рисунке приведена схема хода лучей внутри глазам. Какому дефекту зрения (дальнозоркости или близорукости) соответствует приведенный ход лучей и какие линзы нужны для очков в этом случае?
На рисунке приведена схема хода лучей внутри глазам. Какому дефекту зрения (дальнозоркости или близорукости) соответствует приведенный ход лучей и какие линзы нужны для очков в этом случае?
Решение. Из рисунка видно, что изображение фокусируется не на сетчатке, а ближе к хрусталику, следовательно, близкие предметы человек будет видеть лучше чем далёкие. Для очков требуется рассеивающая линза.
Ответ: близорукость; для коррекции нужны рассеивающие линзы.






 представлены графики зависимости температуры t от времени τ для трёх твёрдых тел одинаковой массы: из алюминия, из меди и из свинца. Тела нагревают на одинаковых горелках. Определите, какой график соответствует нагреванию тела из алюминия, какой — из меди, а какой — из свинца.
представлены графики зависимости температуры t от времени τ для трёх твёрдых тел одинаковой массы: из алюминия, из меди и из свинца. Тела нагревают на одинаковых горелках. Определите, какой график соответствует нагреванию тела из алюминия, какой — из меди, а какой — из свинца. представлены графики нагревания и плавления двух твёрдых веществ — «1» и «2» — одинаковой массы, взятых при одинаковой начальной температуре. Образцы нагреваются на одинаковых горелках. Сравните удельные теплоёмкости этих двух веществ и температуры их плавления.
представлены графики нагревания и плавления двух твёрдых веществ — «1» и «2» — одинаковой массы, взятых при одинаковой начальной температуре. Образцы нагреваются на одинаковых горелках. Сравните удельные теплоёмкости этих двух веществ и температуры их плавления. представлен график зависимости температуры от времени для процесса нагревания воды при нормальном атмосферном давлении. Первоначально вода находилась в твёрдом состоянии.
представлен график зависимости температуры от времени для процесса нагревания воды при нормальном атмосферном давлении. Первоначально вода находилась в твёрдом состоянии. представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания? Удельную теплоёмкость свинца считать равной 130 Дж/кг∙°С
представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания? Удельную теплоёмкость свинца считать равной 130 Дж/кг∙°С приведён график зависимости температуры t воды от времени τ при нормальном атмосферном давлении.
приведён график зависимости температуры t воды от времени τ при нормальном атмосферном давлении. зависимости температуры воды от времени. Начальная температура воды 50 °С. В каком состоянии находится вода в момент времени τ1?
зависимости температуры воды от времени. Начальная температура воды 50 °С. В каком состоянии находится вода в момент времени τ1? приведен график зависимости температуры спирта от времени при его охлаждении и последующем нагревании. Первоначально спирт находился в газообразном состоянии. Какой участок графика соответствует процессу конденсации спирта?
приведен график зависимости температуры спирта от времени при его охлаждении и последующем нагревании. Первоначально спирт находился в газообразном состоянии. Какой участок графика соответствует процессу конденсации спирта? Линейка при этом поворачивалась вслед за палочкой. Почему?
Линейка при этом поворачивалась вслед за палочкой. Почему? соединенных проводником, поднесли отрицательно заряженную палочку. Как распределится заряд на электрометрах?
соединенных проводником, поднесли отрицательно заряженную палочку. Как распределится заряд на электрометрах? расположены заряды q1 = q, q2 = 2q и q3 = 3q .Для каких зарядов сила электрического взаимодействия, действующая между ними, максимальна?
расположены заряды q1 = q, q2 = 2q и q3 = 3q .Для каких зарядов сила электрического взаимодействия, действующая между ними, максимальна? расположены равные по модулю заряды q1, q2 и q3. Какому вектору сонаправлена суммарная сила, действующая на заряд q1 со стороны зарядов q2 и q3?
расположены равные по модулю заряды q1, q2 и q3. Какому вектору сонаправлена суммарная сила, действующая на заряд q1 со стороны зарядов q2 и q3? Оба шарика заряжены положительно. Какой из векторов, изображённых на рисунке, правильно указывает направление электрической силы, действующей на шарик В со стороны шарика A?
Оба шарика заряжены положительно. Какой из векторов, изображённых на рисунке, правильно указывает направление электрической силы, действующей на шарик В со стороны шарика A? соединяющий электроскопы?
соединяющий электроскопы? , изготовленных из различных материалов и имеющих различные размеры Наименьшее электрическое сопротивление имеет(-ют)
, изготовленных из различных материалов и имеющих различные размеры Наименьшее электрическое сопротивление имеет(-ют)
 схема которой приведена на рисунке?
схема которой приведена на рисунке? вольтметр V1 показывает напряжение 2 В, вольтметр V2 — напряжение 0,5 В. Чему равно напряжение на лампе?
вольтметр V1 показывает напряжение 2 В, вольтметр V2 — напряжение 0,5 В. Чему равно напряжение на лампе? подсоединили две лампы, имеющие одинаковые электрические сопротивления. Чему равна мощность электрического тока, потребляемая каждой лампой, если показания идеального амперметра и вольтметра равны соответственно 3 А и 6 В ?
подсоединили две лампы, имеющие одинаковые электрические сопротивления. Чему равна мощность электрического тока, потребляемая каждой лампой, если показания идеального амперметра и вольтметра равны соответственно 3 А и 6 В ?
 показаны два графика зависимости напряжения U на концах двух проводников — «1» и «2» — от силы тока I в них. Эти проводники соединили последовательно. Чему равно общее сопротивление проводников?
показаны два графика зависимости напряжения U на концах двух проводников — «1» и «2» — от силы тока I в них. Эти проводники соединили последовательно. Чему равно общее сопротивление проводников? На рисунке представлена картина линий магнитного поля от двух полосовых магнитов, полученная с помощью железных опилок. Каким полюсам полосовых магнитов, судя по расположению магнитной стрелки, соответствуют области 1 и 2?
На рисунке представлена картина линий магнитного поля от двух полосовых магнитов, полученная с помощью железных опилок. Каким полюсам полосовых магнитов, судя по расположению магнитной стрелки, соответствуют области 1 и 2? (ток направлен «на нас»). В какой точке вектор индукции магнитного поля, создаваемого током, направлен влево (в плоскости рисунка)?
(ток направлен «на нас»). В какой точке вектор индукции магнитного поля, создаваемого током, направлен влево (в плоскости рисунка)? изображены точечный источник света L, предмет K и экран, на котором получают тень от предмета. Как изменятся размеры тени о мере удаления предмета от источника света и приближения его к экрану?
изображены точечный источник света L, предмет K и экран, на котором получают тень от предмета. Как изменятся размеры тени о мере удаления предмета от источника света и приближения его к экрану?

 На рисунке приведена схема хода лучей внутри глазам. Какому дефекту зрения (дальнозоркости или близорукости) соответствует приведенный ход лучей и какие линзы нужны для очков в этом случае?
На рисунке приведена схема хода лучей внутри глазам. Какому дефекту зрения (дальнозоркости или близорукости) соответствует приведенный ход лучей и какие линзы нужны для очков в этом случае?



















