Тригонометрия вокруг нас.

Индивидуальный проект по теме: “Тригонометрия вокруг нас”

Выполнил:

ученик 10 А класса

Першин Никита

Научный руководитель:

Сухненко Ирина Александровна,

учитель математики

Актуальность проекта

Актуальность заключается в том , что знания тригонометрии откроют новые способы решения различных задач во многих областях науки и упростят понимание некоторых аспектов различных наук.

Цель проекта

Узнать ученых , принявших участие в усовершенствовании тригонометрии . Изучить основные методы применения тригонометрии в различных науках.

Задачи проекта

1) Изучить литературу по данной теме.

2) Узнать о применениях тригонометрии в различных науках.

3) Проанализировать решение задач с использованием тригонометрии.

Почему знания тригонометрии необходимы для современного человека?

Большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.

Определение тригонометрии

Тригонометрия (от греч. trigonon – треугольник, metro – метрия) – раздел математики , в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраические тождества тригонометрических функций.

История тригонометрии

Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.). Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э. Вполне возможно, что китайцы открыли его независимо (см. «Математика в девяти книгах»); неясно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался.

В XVII – XIX вв. тригонометрия становится

одной из глав математического анализа.

Она находит большое применение в механике,

физике и технике, особенно при изучении колебательных движений и других

периодических процессов.

Франсуа Виет доказал, что всякое периодическое движение может быть представлено (с любой степенью точности) в виде суммы простых гармонических колебаний.

Разработал учение

о тригонометрических функциях

любого аргумента.

В XIX веке продолжил развитии

Теории тригонометрических функций

Геометрические рассмотрения,-пишет Лобачевский,- необходимы до тех пор в начале тригонометрии, покуда они не послужат к открытию отличительного свойства тригонометрических функций… Отсюда делается тригонометрия совершенно независимой от геометрии и имеет все достоинства анализа».

Стадии развития

1) Тригонометрия была вызвана к жизни необходимостью производить измерения углов.

2) Первыми шагами тригонометрии было установление связей между величиной угла и отношением специально построенных отрезков прямых. Результат - возможность решать плоские треугольники.

3) Тригонометрические функции превращались в самостоятельные объекты исследований.

4)В XVIII в. тригонометрические функции были включены

в систему математического анализа.

Применение тригонометрии в биологии

1) Создание формулы для ускорения установки диагноза:

В результате исследования, проведенного студентом иранского университета Шираз

Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить

информацию, относящуюся к электрической активности сердца или, другими

словами, электрокардиографии.  Формула, получившая название тегеранской, была представлена на многих конференциях по вопросам применения компьютерной техники в кардиологии,

состоявшейся в Нидерландах.  Эта формула представляет собой комплексное алгебраически-тригонометрическое

равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных

параметров, включая несколько дополнительных для расчетов в случаях аритмии.

Как утверждают медики, эта формула в значительной степени облегчает процесс

описания основных параметров деятельности сердца, ускоряя, тем самым,

постановку диагноза и начало собственно лечения.

2) При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.

Применение тригонометрии в астрономии

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Больших успехов достигла

тригонометрия и у индийских средневековых астрономов.

Одним из главных их достижений стала замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника.

Так в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Применение тригонометрии в физике

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений:

Гармонические колебания

Механические колебания

Гармонические колебании

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.

Например, гармонически колеблется величина, изменяющаяся во времени следующим образом: x(t)=Asin(wt+φ) Или x(t)=Acos(wt+φ)

Где х - значение изменяющейся величины, t - время, А - амплитуда колебаний, ω - циклическая частота колебаний, (wt+ φ) - полная фаза колебаний, r  - начальная фаза колебаний..

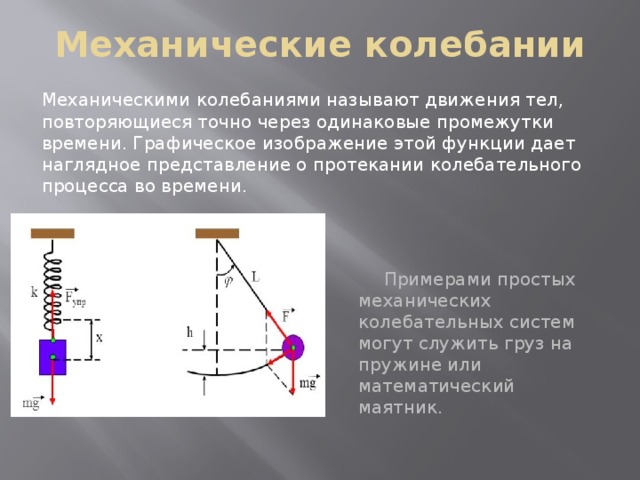
Механические колебании

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.

Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.

Примеры решения задач в физике с использованием тригонометрии

Задача 1

По прямой бежит кролик, его скорость все время равна . В точке,

отстоящей на L от этой прямой, сидит лиса. Она замечает кролика и

бросается в погоню, когда тот находится на минимальном расстоянии от

упомянутой точки. Лиса бежит с такой же по величине скоростью, вектор

скорости лисы направлен в любой момент в точку, где находится кролик.

Найди максимальное ускорение лисы в процессе погони. Лису и кролика

считать материальными точками.

Решение

Перейдем в систему отсчету, связанную с кроликом. В этой системе

ускорение лисы такое же, как и в неподвижной системе отсчета.

Проведем расчет для точки A (1 рисунок). Пусть угол AOB = α, OA = L.

Сумма расстояний OA + AB = L.

Ускорение лисы определяется вращением вектора ,

направленного вдоль биссектрисы угла, образованного двумя вектора .

Выберем интервал времени Δ t и рассмотрим треугольник AOB(рисунок 2).

Тогда, по теореме синусов,

или

Отсюда находим угловую скорость:

и ускорение:

Исследуем полученное выражение для ускорения на максимум:

Задача 2

Камень брошен на склоне горы под углом α к ее поверхности. Определите дальность полета камня, если начальная скорость камня равна , угол наклона горы к горизонту β. Сопротивление воздуха не учитывать.

Решение.  Сложное движение камня по параболе нужно представить как результат наложения двух прямолинейных движений: одного вдоль поверхности Земли, другого - по нормали к ней.

Выберем прямоугольную систему координат с началом отсчета в точке бросания камня так, чтобы оси OX и OY совпали с указанными направлениями, и найдем составляющие векторов начальной скорости v 0  и ускорения свободного падения g по осям. Проекции этих составляющих на оси  OX  и  OY  равны соответственно:

После этого сложное движение можно рассматривать как два более простых:

равнозамедленное движение вдоль поверхности Земли с ускорением 

и равнопеременное движение, перпендикулярное склону горы, с ускорением

Составляем уравнения движения для каждого направления с учетом того, что за

время t всего движения перемещение камня по нормали к поверхности (по оси  OY ) оказалось равным нулю, а вдоль поверхности (по оси  OX ) - равным s:

(1) (2)

Из первого уравнения определяем время полета камня:

Подставляя это выражение во второе уравнение, находим:

Заключение

Мы рассмотрели лишь малую часть того, где можно

встретить тригонометрические функции.

Мы выяснили, что тригонометрия была вызвана к жизни 

необходимостью производить измерения углов, но со 

временем развилась и в науку о тригонометрических 

функциях.

Мы доказали, что тригонометрия тесно связана с физикой, встречается в природе и медицине. Можно приводить 

бесконечно много примеров периодических процессов 

живой и неживой природы. Все периодические 

процессы можно описать с помощью тригонометрических функций и изобразить на графиках.

Спасибо за внимание!!!