

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

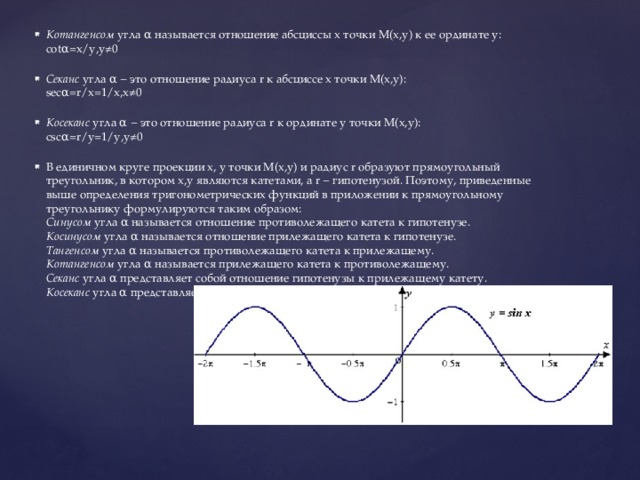
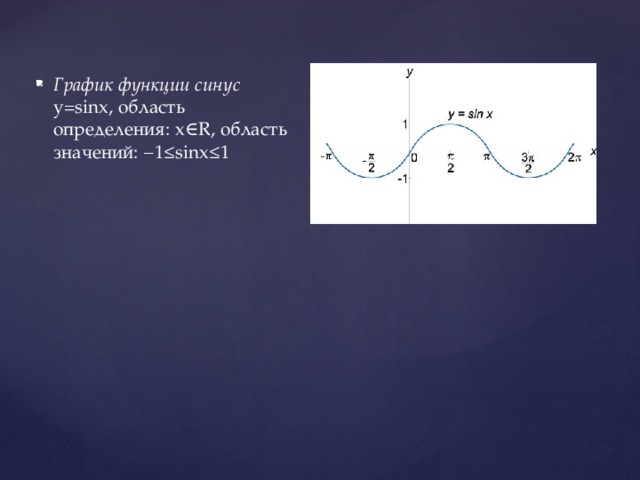
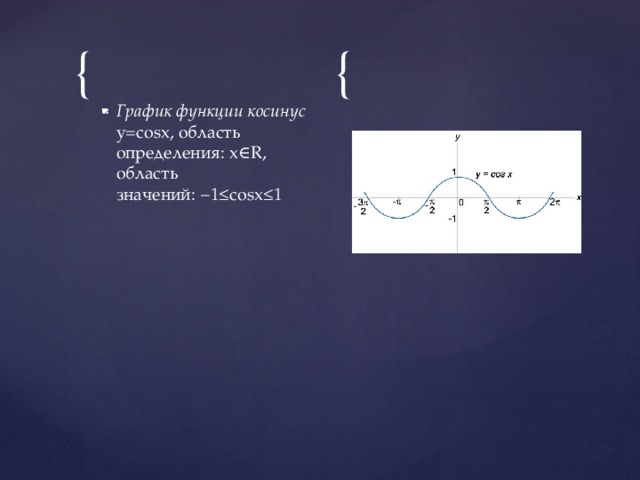
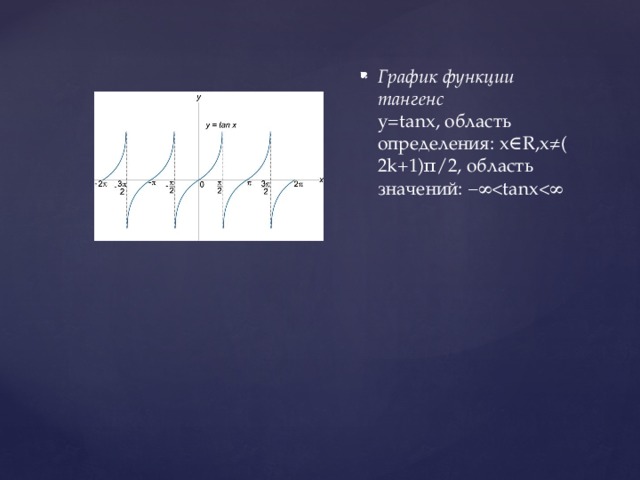
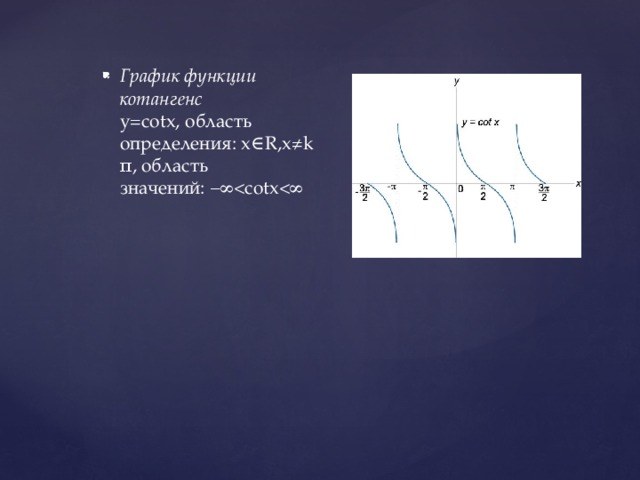
Тригонометрическая функция
Категория:
Математика
12.01.2019 17:39








![График функции секанс y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞)](https://fsd.multiurok.ru/html/2019/01/12/s_5c39fc2f0b834/img9.jpg)
![График функции косеканс y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞)](https://fsd.multiurok.ru/html/2019/01/12/s_5c39fc2f0b834/img10.jpg)










