Тригонометрия - это раздел математики, изучающий тригонометрические функции.

История
Тригонометрия – (от греч. Trigwnon-треугольник и metrew- измеряю)
По звездам вычисляли
местонахождение корабля в
море.
Древние люди вычисляли
высоту дерева,
сравнивая длину его тени с
длиной тени от шеста,
высота которого была известна.

Древняя Греция
Потребность в решении треугольников раньше всего возникла в астрономии: и в течении долгого времени тригонометрия развивалась и изучалась как один из отделов астрономии. Способы решения треугольников (сферических) первые были письменно изложены греческим астрономом Гиппархом в середине 2 века до н.э. Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею (2 век н.э.), создателю геоцентрической системы мира.

Индия
В Индии было положено начало тригонометрии как учению о тригонометрических величинах. Индийские ученые пользовались различными тригонометрическими соотношениями, в том числе и теми, которые используются в современной науке.

Значимые люди в тригонометрии
- Таблица числовых значений хорд
- Таблица для определения соотношений между элементами треугольников
Гиппарх Никейский
( 180 – 125 г. до н.э.)
- Первая таблица синусов, высчитанная по хордам в окружности
- «Альмагест» – самая значимая тригонометрическая работа всей античности
Клавдий Птолемей (90 – 168 г н.э)

- Построил таблицы тангенсов, котангенсов и косекансов
Ал-Батани
( ок. 900 г. н.э)
- Дал определения тригонометрическим функциям
- Установил формулу двойного угла
Абу-ль-Вефа
( 940 – 997 г. н.э)

- Автор трактата о полном четырехстороннике
Насир-эд-Дин из Туса
(1201 – 1274 г. н.э)
- Построил таблицы синусов и котангенсов
Ал-Хорезми
(783 – 850 г. н.э)

- Дополнил и систематизировал различные случаи решения плоских и сферических треугольников
- Доказал«плоскую» теорему косинусов
Франсуа Виет (1540 – 1603 г.)
- Разложил функции в ряды и открыл путь для их использования в математическом анализе
Исаак Ньютон
(1643 – 1727г.)

- Ввел понятие функции и принятую в наши дни символику
- Разъяснил вопрос о знаках всех тригонометрических функций любого аргумента
Леонард Эйлер
(1707 – 1783 г. н.э)
- Выразил тригонометрические функции как отношение координат x, y, z к длине элемента.
Ричард Саусвелл (1888-1970)

Тригонометрия в физике
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями .
Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания :

Тригонометрия и тригонометрические функции в медицине и биологии.
Одно из фундаментальных свойств живой природы - это цикличность большинства происходящих в ней процессов.
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
Модель биоритмов можно построить с помощью тригонометрических функций.
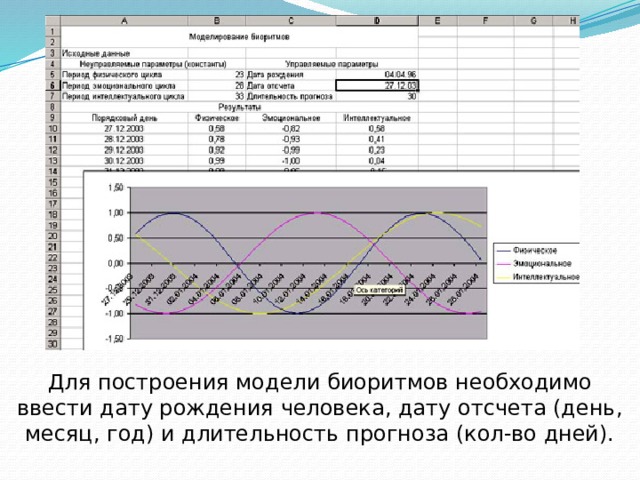
Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
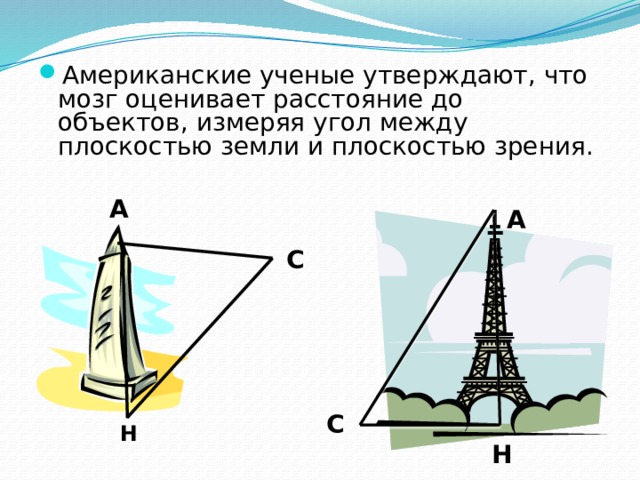
- Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
А
А
С
С
Н
Н

При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.

При полёте птицы траектория взмаха крыльев образует синусоиду.

Теория радуги
Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
n 1 - показатель преломления первой среды n 2 - показатель преломления второй среды
α -угол падения, β -угол преломления света
sin α / sin β = n 1 / n 2

Северное сияние
Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

Тригонометрия в музыке
- Согласно дошедшим из древности сведениям, первыми, кто попытался сделать это, были Пифагор и его ученики.
одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
- диатоническая гамма 2:3:5

Тетраэдр из различных типов аккордов четырех звуков:
синий – малые интервалы;
более теплые тона - более «разряженные» звуки аккорда; красная сфера- наиболее гармоничный аккорд с равными интервалами между нотами.

Тригонометрия в архитектуре
Детская школа Гауди в Барселоне

Сантьяго Калатрава Винодельня «Бодегас Исиос»

Страховая корпорация Swiss Re в Лондоне
x = λ
y = f ( λ )cos θ
z = f ( λ )sin θ

Феликс Кандела Ресторан в Лос-Манантиалесе

Заключение
- Мы выяснили , что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
- Мы доказали , что тригонометрия тесно связана с физикой, встречается в природе, музыке, архитектуре и медицине.
- Мы думаем , что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.

Спасибо за внимание.


















































