Тригонометрические функции. Графики

Графики тригонометрических функций и их свойства

• Функция у = sin x, ее свойства

• Функция у = cos x

• Преобразование графиков тригонометрических функций путем параллельного переноса
• Преобразование графиков тригонометрических функций путем сжатия и расширения

• Преобразование графиков тригонометрических функций путем зеркального отражения относительно оси абсцисс
• Построение графика функции гармонических колебаний
• y=A sin( ω x+ φ 0 )
• Построение графика y=sin x с помощью числового круга

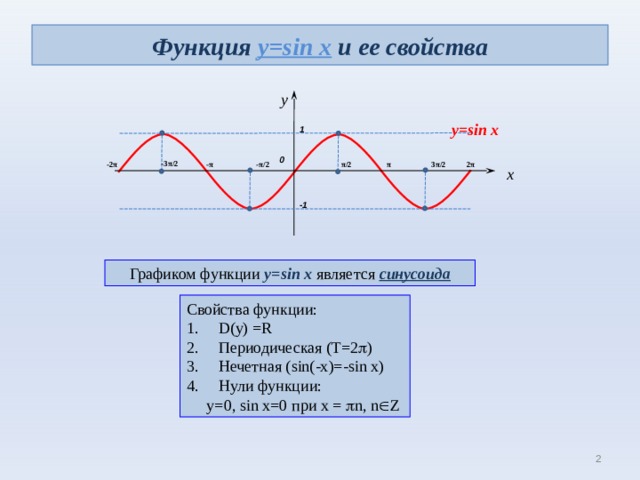
Функция y=sin x и ее свойства

y

y=sin x

1

0

-3 π /2

3 π /2

π /2

- 2 π

2 π

- π /2

- π

π

x

-1

Графиком функции y=sin x является синусоида

Свойства функции:

• D(y) =R
• Периодическая (Т=2  )
• Нечетная ( sin(-x)=-sin x)
• Нули функции:

у=0, sin x=0 при х =  n, n  Z

2

0 при х   (0+2  n ;  +2  n ) , n  Z У y y=sin x 1 0 -3 π /2 π /2 - 2 π 2 π 3 π /2 - π /2 - π π x -1 6. Промежутки монотонности: функция возрастает на промежутках вида:  -  /2 +2  n ;  / 2+2  n   n  Z функция убывает на промежутках вида:  /2 +2  n ; 3  / 2+2  n   n  Z 3 3 " width="640"

y

1

y=sin x

0

-3 π /2

2 π

π /2

π

- π

- π /2

3 π /2

- 2 π

x

-1

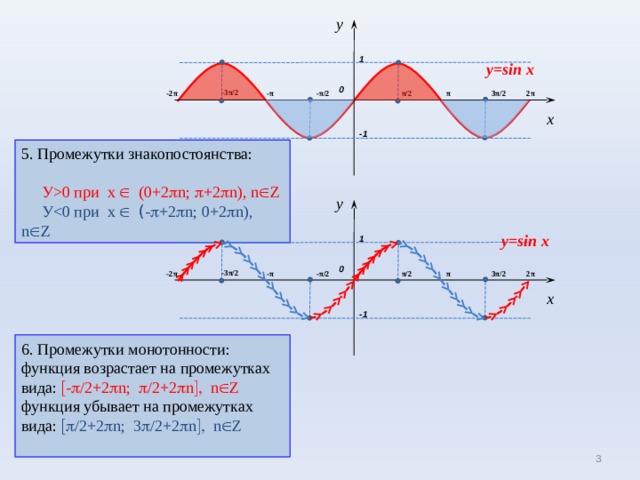
5. Промежутки знакопостоянства:

У 0 при х   (0+2  n ;  +2  n ) , n  Z

У

y

y=sin x

1

0

-3 π /2

π /2

- 2 π

2 π

3 π /2

- π /2

- π

π

x

-1

6. Промежутки монотонности:

функция возрастает на промежутках

вида:  -  /2 +2  n ;  / 2+2  n   n  Z

функция убывает на промежутках

вида:  /2 +2  n ; 3  / 2+2  n   n  Z

3

3

y

y=sin x

x мах

x мах

1

0

-3 π /2

π

π /2

3 π /2

2 π

- 2 π

- π

- π /2

x

-1

x min

x min

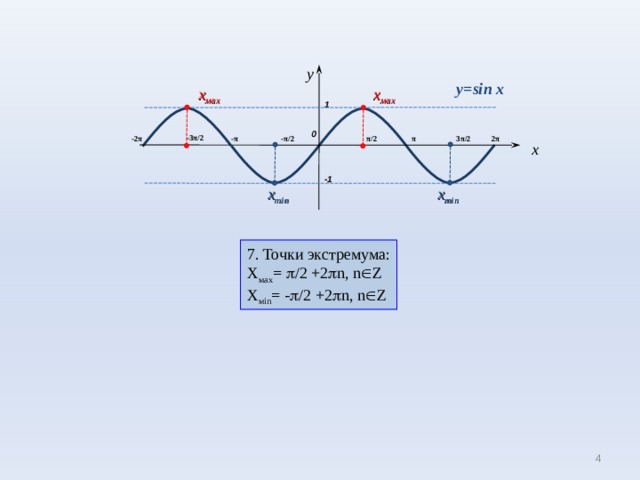
7. Точки экстремума:

Х мах =  / 2 +2  n , n  Z

Х м in = -  / 2 +2  n , n  Z

4

4

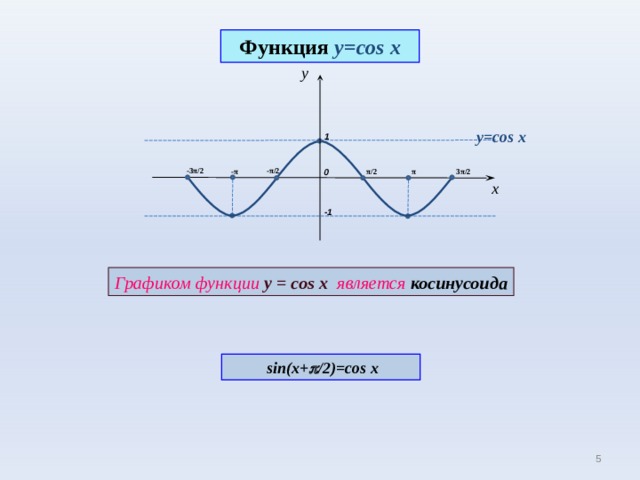
Функция y = cos x

y

y=cos x

1

-3 π /2

- π /2

π /2

3 π /2

0

- π

π

x

-1

Графиком функции у = cos x является косинусоида

sin(x+  /2)=cos x

5

5

0 при х   (-   +2  n ;   +2  n ) , n  Z У 6. Промежутки монотонности: функция возрастает на промежутках вида:  +2  n ; 2  +2  n   n  Z функция убывает на промежутках вида:   +2  n ;  +2  n   n  Z 7. Точки экстремума: Х мах =  +2  n , n  Z Х м in =  +2  n , n  Z 5 " width="640"

Свойства функции y = cos x

• D(y) =R
• Периодическая Т=2 
• Четная cos(-x)=cos x
• Нули функции:

у=0, cos x=0 при х = 1/2  n, n  Z

5. Промежутки знакопостоянства:

У 0 при х   (-   +2  n ;   +2  n ) , n  Z

У

6. Промежутки монотонности:

функция возрастает на промежутках вида:

 +2  n ; 2  +2  n   n  Z

функция убывает на промежутках вида:

  +2  n ;  +2  n   n  Z

7. Точки экстремума:

Х мах =  +2  n , n  Z

Х м in =  +2  n , n  Z

5

Преобразование графиков тригонометрических функций путем параллельного переноса

• График функции у = f (x +в) получается из графика функции

у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс

• График функции у = f (x )+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат

5

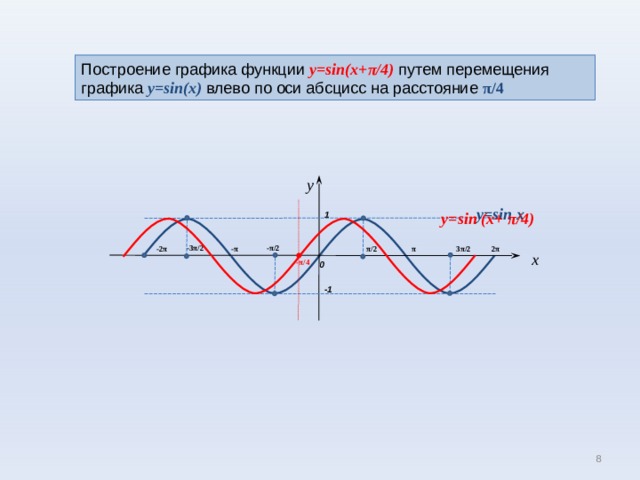
Построение графика функции y=sin(x+ π /4) путем перемещения графика y=sin(x) влево по оси абсцисс на расстояние π /4

y

y=sin x

y=sin (x+ π /4)

1

-3 π /2

- π /2

- 2 π

- π

3 π /2

2 π

π

π /2

x

- π /4

0

-1

8

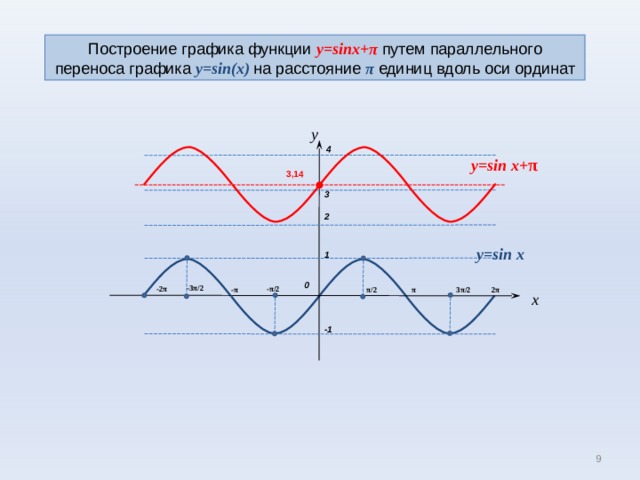
Построение графика функции y=sinx+ π путем параллельного переноса графика y=sin(x) на расстояние π единиц вдоль оси ординат

y

4

y=sin x + π

3 ,14

3

2

y=sin x

1

0

-3 π /2

- π /2

- 2 π

3 π /2

- π

2 π

π

π /2

x

-1

9

1) вдоль оси ординат График функции у = k f (x ) получается из графика функции у = f(x) путем его сжатия в k раз (при 09 " width="640"

Преобразование графиков тригонометрических функций путем сжатия и растяжения

• График функции у = k f (x ) получается из графика функции у = f(x) путем его растяжения в k раз (при k1) вдоль оси ординат
• График функции у = k f (x ) получается из графика функции у = f(x) путем его сжатия в k раз (при 0

9

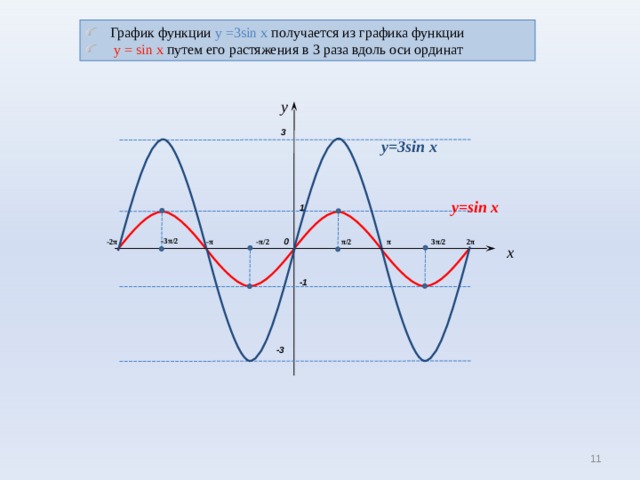
• График функции у = 3sin x получается из графика функции
• у = sin x путем его растяжения в 3 раза вдоль оси ординат

y

3

y= 3 sin x

y=sin x

1

-3 π /2

0

3 π /2

2 π

- 2 π

- π

π /2

π

- π /2

x

-1

-3

11

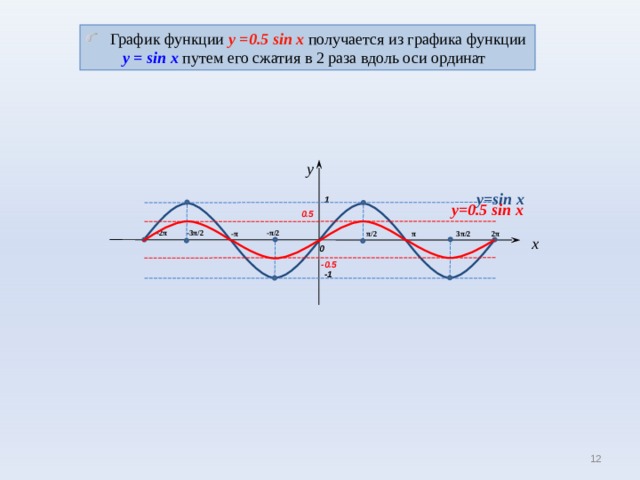
• График функции у = 0. 5 sin x получается из графика функции у = sin x путем его сжатия в 2 раза вдоль оси ординат

y

y=sin x

1

y= 0.5 sin x

0.5

-3 π /2

- π /2

- 2 π

- π

π

3 π /2

2 π

π /2

x

0

- 0.5

-1

11

1) вдоль оси абсцисс График функции у = f (kx ) получается из графика функции у = f(x) путем его растяжения в k раз (при 012 " width="640"

Преобразование графиков тригонометрических функций путем сжатия и растяжения

График функции у = f (kx ) получается из графика функции

у = f(x) путем его сжатия в k раз (при k1) вдоль оси абсцисс

График функции у = f (kx ) получается из графика функции

у = f(x) путем его растяжения в k раз (при 0

12

График функции у = cos (0.5x ) получается из графика функции у = cos x путем его растяжения в 2 раза ( 0

y

T = 2 π

y=cos x

1

y=cos 0.5 x

x

- 2 π

-3 π /2

- π /2

2 π

0

π /2

π

3 π /2

- π

-1

T = 4 π

Видно, что период (T) функции увеличился в 2 раза, т.к. T = 2 π / ω ,

где ω – коэффициент при переменной x ( частота колебаний)

12

1) вдоль оси абсцисс y y=cos x T = 2 π T = 2 π y=cos 2 x 1 - 2 π -3 π /2 - π /2 2 π π π /2 3 π /2 0 - π x -1 Видно, что период (T) функции уменьшился в 2 раза, т.к. T = 2 π / ω , где ω – коэффициент при переменной x ( частота колебаний) 14 " width="640"

График функции у = cos 2x получается из графика функции у = cos x путем его сжатия в 2 раза ( k1) вдоль оси абсцисс

y

y=cos x

T = 2 π

T = 2 π

y=cos 2 x

1

- 2 π

-3 π /2

- π /2

2 π

π

π /2

3 π /2

0

- π

x

-1

Видно, что период (T) функции уменьшился в 2 раза, т.к. T = 2 π / ω ,

где ω – коэффициент при переменной x ( частота колебаний)

14

Преобразование графиков тригонометрических функций путем зеркального отражения относительно оси абсцисс

Графики функций у = -f (kx ) и у=- k f(x) получаются из графиков функций у = f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс

синус – функция нечетная, поэтому sin(-kx) = - sin (kx)

косинус –функция четная, значит cos(-kx) = cos(kx)

15

Графики функций y = - 3 sin x получается из графика функции y = 3 sin x путем ее зеркального отображения относительно оси абсцисс

y

3

y= -3 sin x

1

-3 π /2

0

- 2 π

2 π

3 π /2

- π /2

- π

π

π /2

x

y= 3 sin x

-1

-3

15

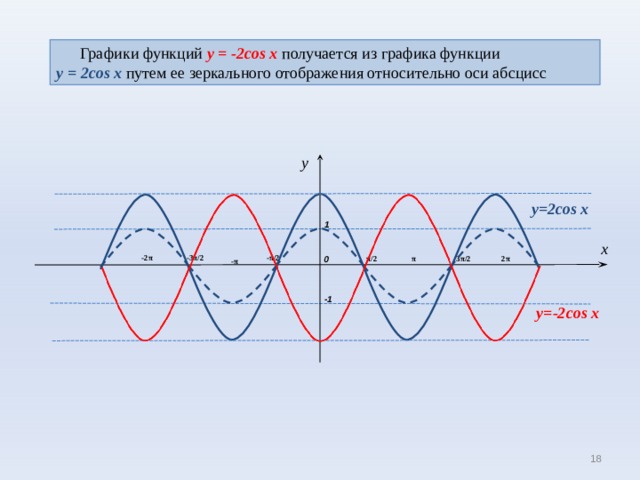
Графики функций y = -2cos x получается из графика функции

y = 2cos x путем ее зеркального отображения относительно оси абсцисс

y

y= 2 cos x

1

x

- 2 π

-3 π /2

- π /2

2 π

3 π /2

π

π /2

0

- π

-1

y= -2 cos x

15

Построение графика функции гармонических колебаний

y=A sin( ω x+ φ 0)

Для примера строим график функции y=3 sin (2x+ π /3) .

Здесь амплитуда колебаний А равняется 3 единицам,

круговая частота колебаний ω равна 2,

а начальная фаза колебаний φ 0 равна π / 3, т.е.:

A=3, ω =2 и φ 0 = π / 3. Период колебаний T =2 π / ω .

15

Последовательность построения графика функции y=3 sin (2x+ π /3)

y

3

2

y=3 sin (2x+ π /3)

y=sin x

y=sin (x+ π /3)

1

y=sin (2x+ π /3)

-3 π /2

- π /2

- 2 π

2 π

3 π /2

- π

π

π /2

x

- π /3

0

-1

-2

-3

• Строим исходный график функции y= sin x

• Используя параллельный перенос сдвигаем график функции y= sin x

влево по оси абсцисс на расстояние π /3

• Сжимаем график функции y= sin ( x + π /3) в 2 раза по оси абсцисс

• Растягиваем график функции y= sin (2 x + π /3) в 3 раза по оси ординат

15

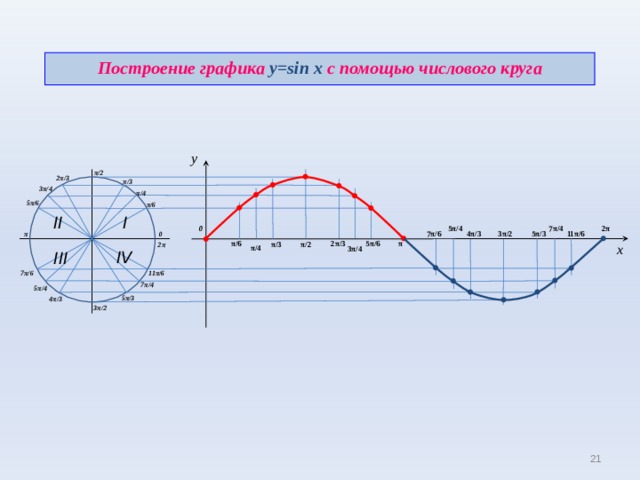
Построение графика y=sin x с помощью числового круга

y

π /2

2 π /3

π /3

3 π /4

π /4

5 π /6

π /6

I

II

0

2 π

5 π /4

7 π /4

7 π /6

11 π /6

5 π /3

4 π /3

3 π /2

0

π

5 π /6

π

π /6

2 π /3

π /3

π /2

x

2 π

π /4

3 π /4

IV

III

11 π /6

7 π /6

7 π /4

5 π /4

5 π /3

4 π /3

3 π /2

20

20