Тригонометрия в жизни человека

Тригонометрия в жизни человека

Тригонометрия в нашей жизни

  Тригонометрия (от греч. Trigwnon -треугольник и metrew - измеряю) – это раздел математики, изучающий тригонометрические функции. Сложно представить, но с этой наукой мы сталкиваемся не только в математике, но и в повседневной жизни, а также в физике, биологии, в медицине, даже в музыке и архитектуре.

Тригонометрия в математике

В настоящее время тригонометрические функции лежат в основе специального математического аппарата, так называемого гармонического анализа, при помощи которого изучаются различного рода периодические процессы: колебательные движения, распространение волн, некоторые атмосферные явления и пр.

Тригонометрия в медицине

Наше сердце, в какой-то степени, не может обойтись без тригонометрии, потому что без электрокардиографии мы бы не могли знать о состоянии нашего сердца, то есть:

·        о наличии аритмии;

·        в норме ли частота сердечных сокращений и ритм сердца;

·        есть ли изменения, указывающие на то, что сердце испытывает кислородное голодание, т.е. его кровоснабжение недостаточно;

·        наблюдается ли гипертрофия (утолщение) тех или иных отделов сердца, что может привести к серьезным последствиям.

Тригонометрия в архитектуре

Тригонометрия широко используется в строительстве, а особенно в архитектуре. Можно привести самый легкий пример в архитектуре: скульптура французского мастера Золотого века искусства. Пропорциональное соотношение в построении статуи было идеально. Но при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Дело в том, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Ситуация меняется, т.к. статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно, и синус угла падения увеличивается. 

Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (тоже самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку зрения.

Тригонометрия

помогает нашему мозгу определять расстояния до объектов, измеряя угол между плоскостью земли и плоскостью зрения.

Применение тригонометрии

Существует множество областей, в которых применяются тригонометрия и тригономет рические функции. Например, метод  триангуляции  используется в  астрономии  для измерения расстояния до ближайших звезд, в  географии  для измерения расстояний между объектами, а также в  спутниковых навигационных системах .  Синус  и  косинус  имеют фундаментальное значение для теории  периодических функций , например при описании звуковых и световых волн.

Тригонометрия в астрономии

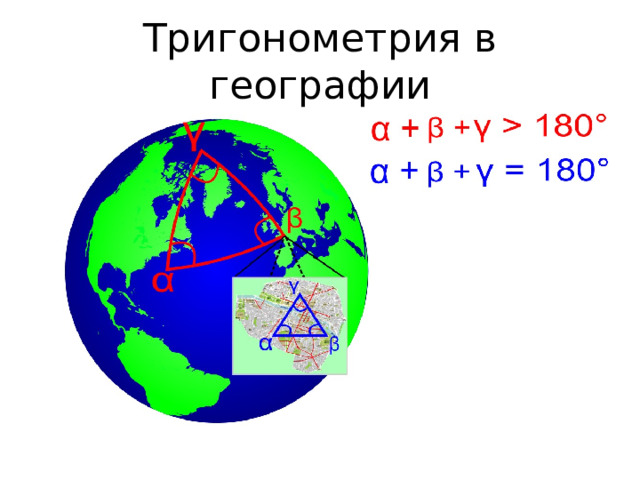
Тригонометрия в географии

Тригонометрия в спутниковых навигационных системах

Описание звуковых волн с помощью тригонометрии

Тригонометрия прошла длинный путь развития. Она была придумана с целью производить измерения углов, но со временем развилась и в науку о тригонометрии. Мы можем сказать, что тригонометрия не зависит от других наук, а другие науки зависят от тригонометрии.

Благодарю за внимание!