Трыганаметрычныя функцыі

«Трыганаметрычныя функцыі, іх ўласцівасці і графікі».

(абагульняючы ўрок па тэме)

Мэты:

1. Развіццё пазнавальнай цікавасці да навучання.

2. Ужыванне матэматычнага мадэлявання як спосабу актывізацыі аналітычнага мыслення.

3. Фарміраванне практычных навыкаў пабудовы графікаў функцый на аснове вывучанага тэарэтычнага матэрыялу.

Задачы:

1. Выкарыстоўваць існуючы патэнцыял ведаў пра ўласцівасці функцый у канкрэтных сітуацыях.

2. Умець адстойваць свой пункт гледжання.

3. Ужываць ўсвядомленае ўсталяванне сувязяў паміж аналітычнай і геаметрычнай мадэлямі трыганаметрычных функцый.

Ход ўрока.

І. Арганізацыйны момант.

ІІ. Вусныя практыкаванні (франтальна).

1. Праверце, ці належыць графікам функцый:

А) у = sin x пункт з каардынатамі (π; 0),

Б) у = cos x пункт з каардынатамі (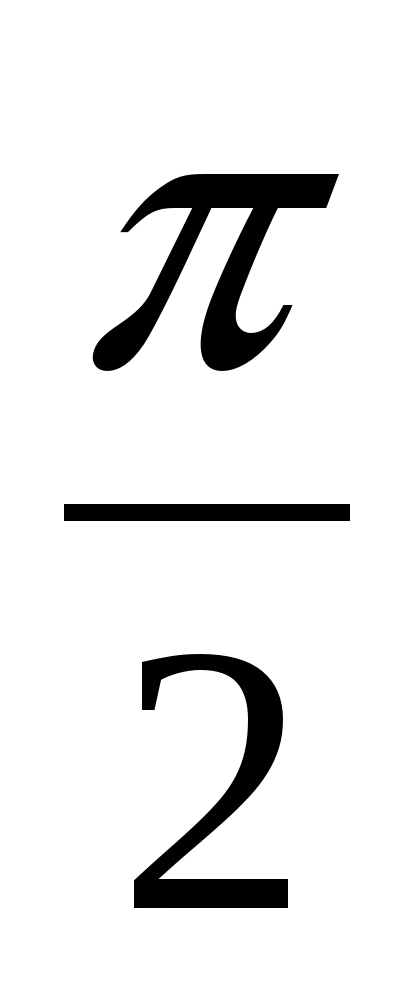; 1).

1. Знайсці найбольшае і найменшае значэнні функцый:

А) у = sin x на адрэзку ,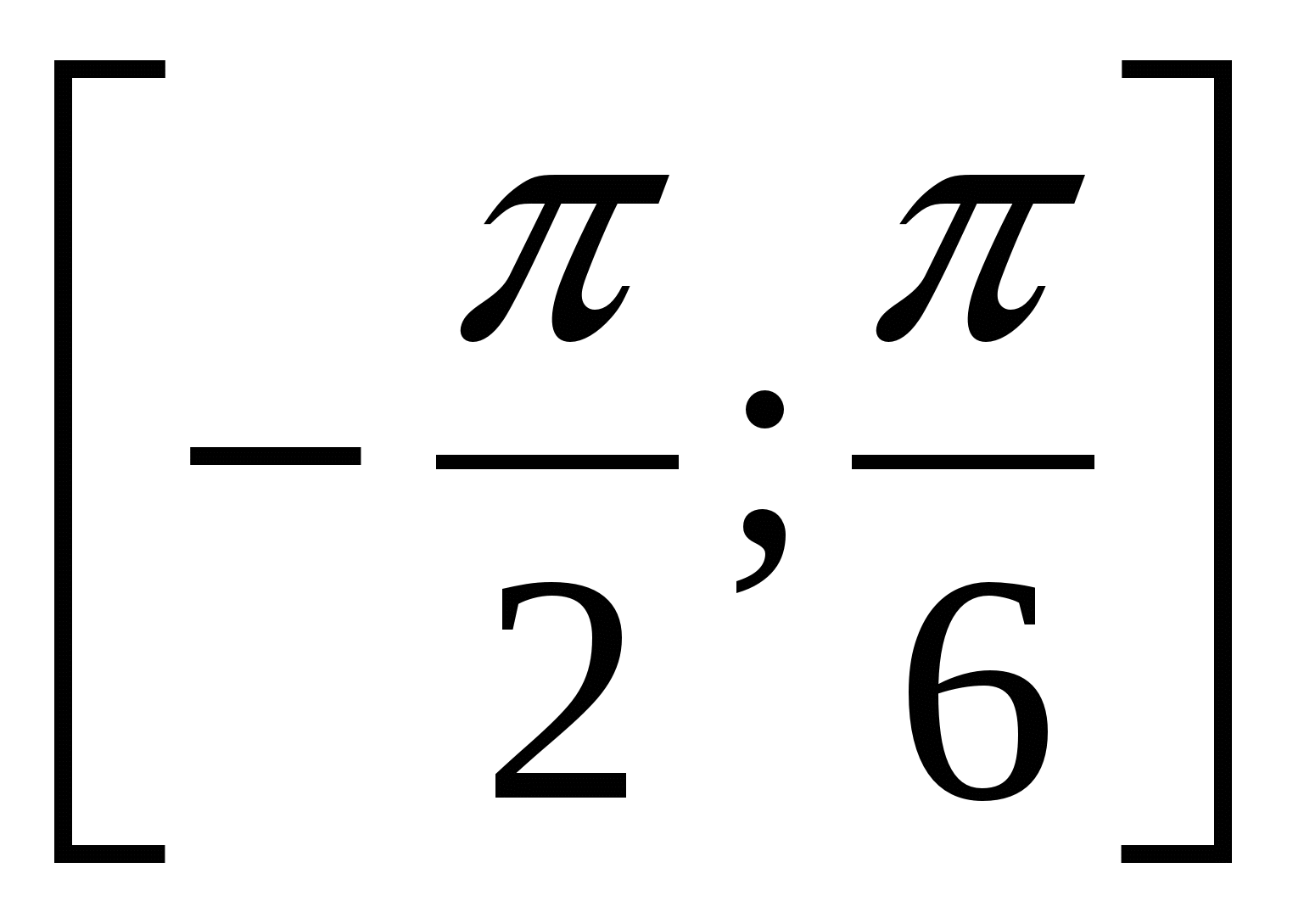

Б) у = cos x на паўінтэрвале ,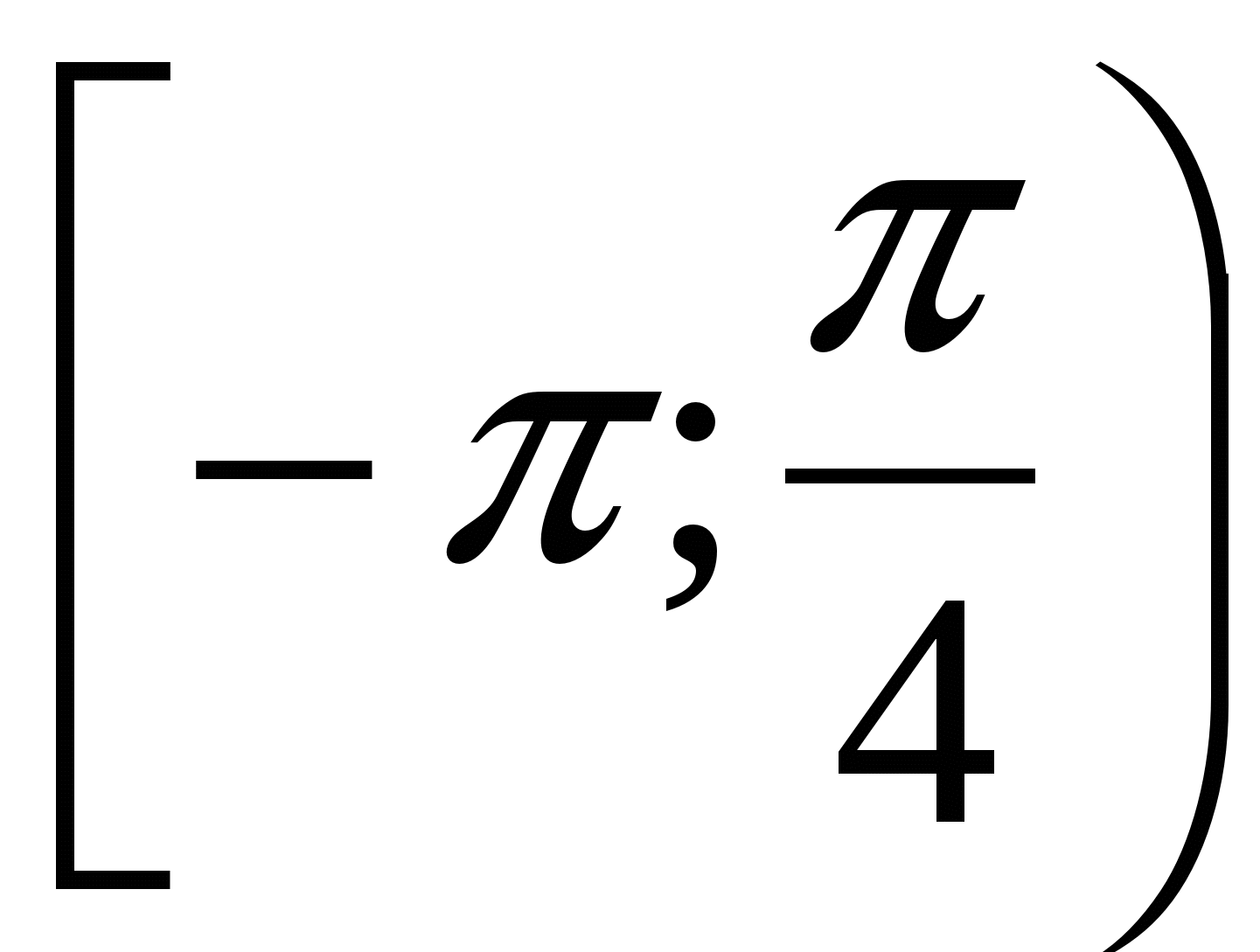

В) у = tg х на паўінтэрвале.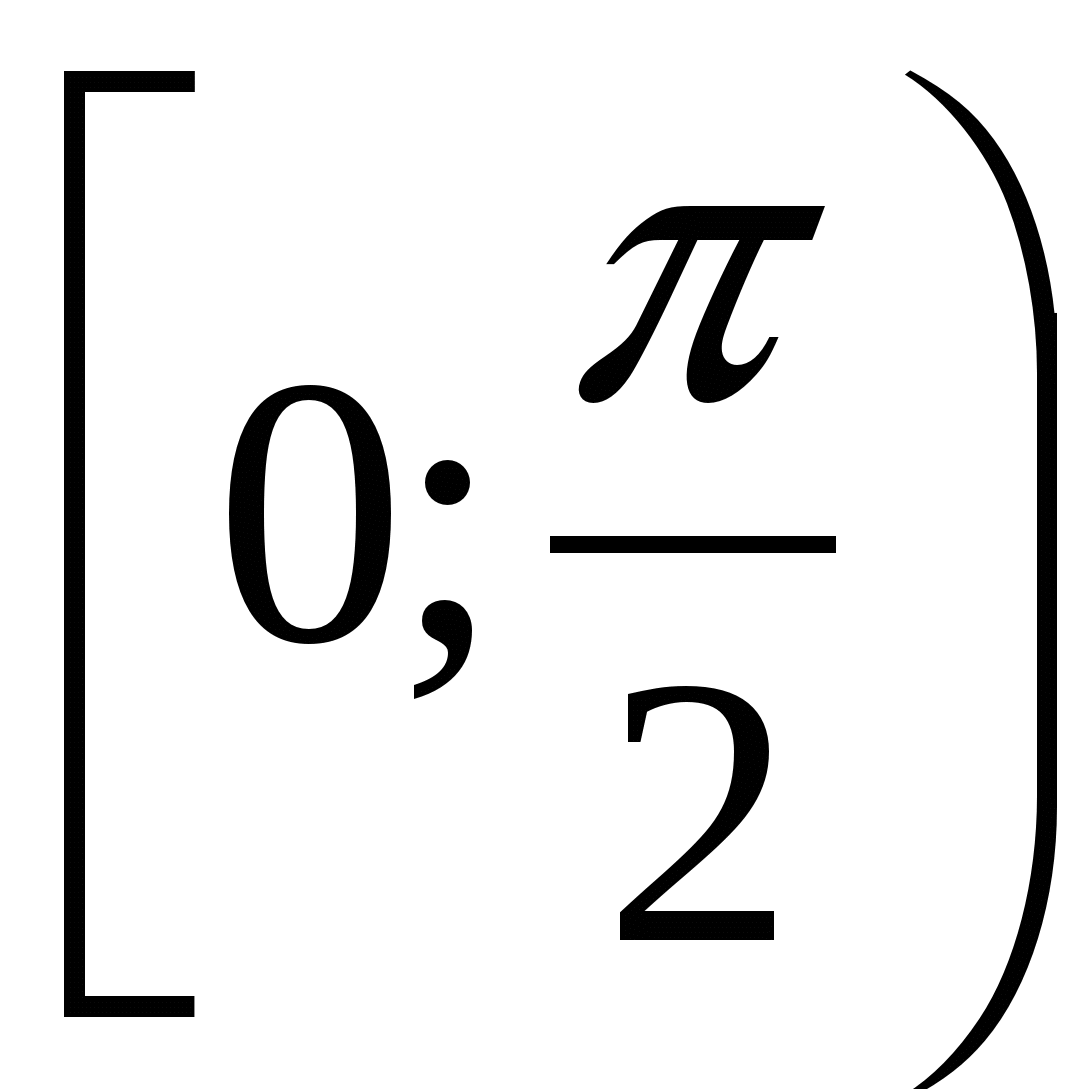

3) Рашыце ўраўненні: cos x = 0, tg х = -1, sin x = 2.

4) Ці з'яўляецца лік 15π перыядам функцый: у = sin x, у = cos x, у = tgх? Назавіце асноўны перыяд гэтых функцый.

ІІІ. Размінка

Рашыць ураўненне : cos(4х-25) = -1

ІV. Практычная работа

А) Рашыце графічна ўраўненне sin x = cos x.

V.Работа з падручнікам

№ 3.30(2) Адказ: ( )

VІ. Самастойная работа

1. Пабудаваць графік функцыі: у = 2 sin x – 1 ( у = 3 cos х)

2. Знайсці найбольшае і найменшае значэнні гэтых функцый.

3. Праверце, ці належаць графіку функцыі пункты з каардынатамі

(π;0), (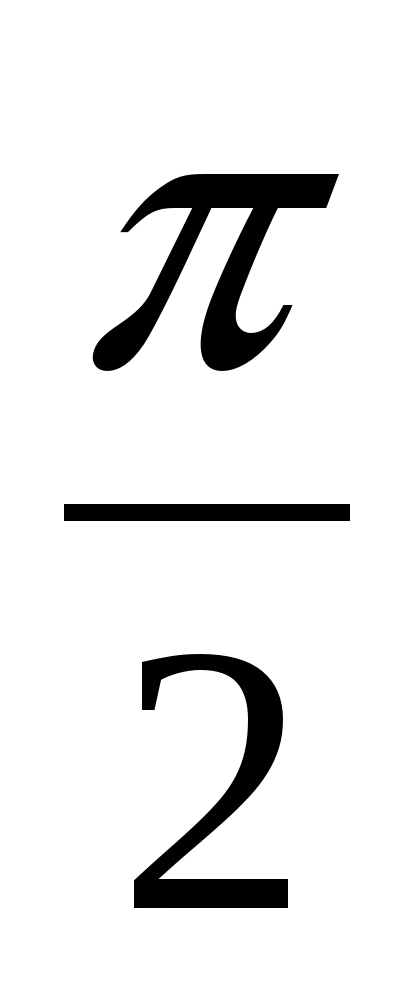; 1).

4. Рашыце ўраўненні: 2 sin x – 1 = 0. 3 cos 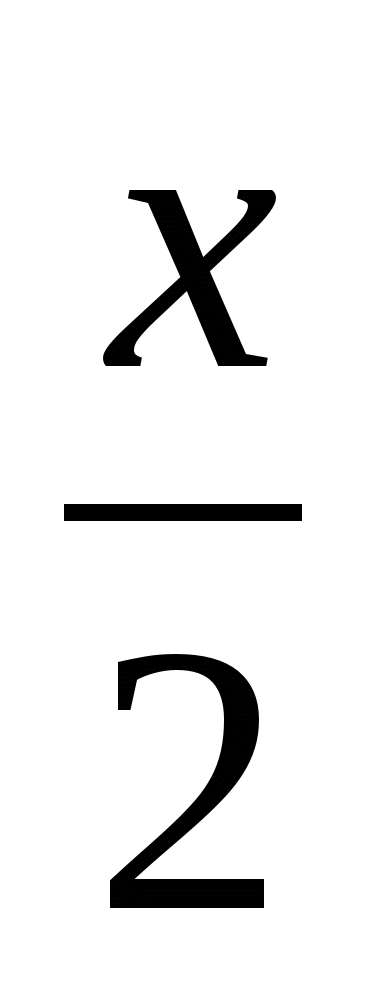 = 1/3.

VІІ. Рэфлексія

1. Чаму новаму вы навучыліся на ўроку?

2. Над чым яшчэ патрэбна папраць?

VІІІ. Дамашняе заданне: п. п.3.3-3.3.6, № 3.65(1,3), 3.84(ц.)