Творческий исследовательский проект "ПАРКЕТЫ"

Исследовательская работа на тему: «Исследование расположения и геометрических характеристик рисунков различных видов паркета»

Подготовили ученики 8 А класса

МБОУ СОШ №9 Ковалёва Елизавета и Толкочёва Надежда Руководитель: учитель математики

Ковтунова Е.С.

Новозыбков 2017

Введение

Многие из вас, наверняка, встречали рисунки на плоскости, например на полу или потолке. При которых вся плоскость оказывалась замощена различными причудливыми узорами, геометрическими фигурами, либо же изображениями животных или растений. Так вот, при некоторых условиях, данные способы замощения плоскости могут называться паркетом.

Паркет из многоугольников

Паркет из многоугольников – это такое разбиение плоскости на многоугольники, при котором любые два из них имеют общую точку, либо общую прямую, либо же не пересекаются.

Если все многоугольники паркета являются правильными, то такой паркет называется паркетом из правильных многоугольников. Именно данный вид паркетов мы и рассмотрим в нашей работе.

Цели и задачи работы

Цели:

• Исследовать, от чего зависят площади повторяющихся элементов, паркета и вывести формулы для их нахождения.
• Исследовать, от чего зависит количество повторяющихся элементов паркета, и вывести формулы для их нахождения.

Задачи:

• Рассмотреть понятие паркета, различные виды паркетов и способы замощения плоскости с помощью паркета.
• Вывести формулу площади правильного многоугольника.
• Рассмотреть 8 видов полуправильных паркетов
• Вывести формулы для нахождения площадей повторяющихся элементов паркета.
• Вывести формулы для нахождения количества повторяющихся элементов паркета, а также выяснить, от каких геометрических характеристик они зависят .

Объекти предмет ииследования

Объектом нашего исследования являются различные паркеты, состоящие из правильных многоугольников, а предметом – зависимости площадей и количества повторяющихся элементов паркета от его геометрических характеристик и площади, которую требуется замостить.

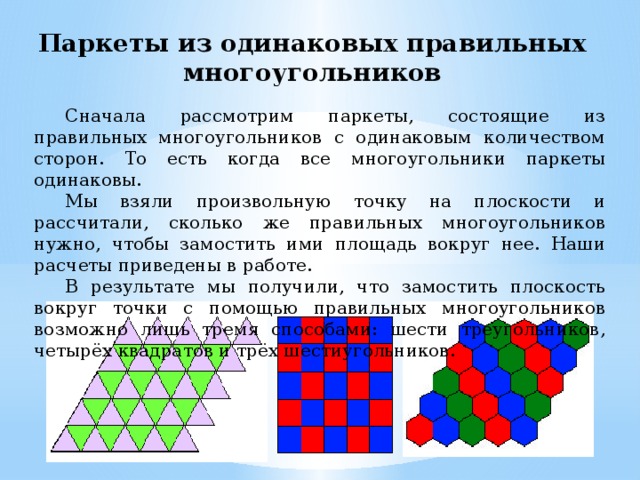
Паркеты из одинаковых правильных многоугольников

Сначала рассмотрим паркеты, состоящие из правильных многоугольников с одинаковым количеством сторон. То есть когда все многоугольники паркеты одинаковы.

Мы взяли произвольную точку на плоскости и рассчитали, сколько же правильных многоугольников нужно, чтобы замостить ими площадь вокруг нее. Наши расчеты приведены в работе.

В результате мы получили, что замостить плоскость вокруг точки с помощью правильных многоугольников возможно лишь тремя способами: шести треугольников, четырёх квадратов и трёх шестиугольников.

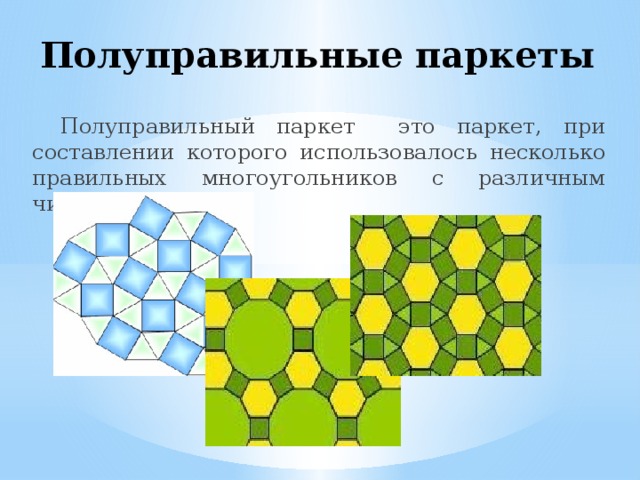
Полуправильные паркеты

Полуправильный паркет это паркет, при составлении которого использовалось несколько правильных многоугольников с различным числом сторон.

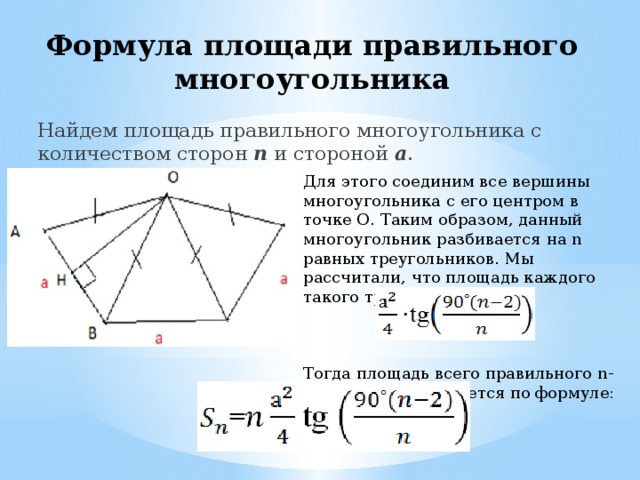
Формула площади правильного многоугольника

Найдем площадь правильного многоугольника с количеством сторон n и стороной a .

Для этого соединим все вершины многоугольника с его центром в точке О. Таким образом, данный многоугольник разбивается на n равных треугольников. Мы рассчитали, что площадь каждого такого треугольника равна

Тогда площадь всего правильного n-угольника вычисляется по формуле:

Площадь и количество повторяющихся элементов 8-ми видов полуправильных паркетов

Далее мы использовали полученную формулу для нахождения площади повторяющихся элементов для 8-ми видов полуправильного паркета.

А затем рассчитали количество правильных элементов, которое необходимо, чтобы уложить данным паркетом площадь, равную S.

Рассчеты представлены в нашей работе. Здесь мы приведем лишь полученные результаты.

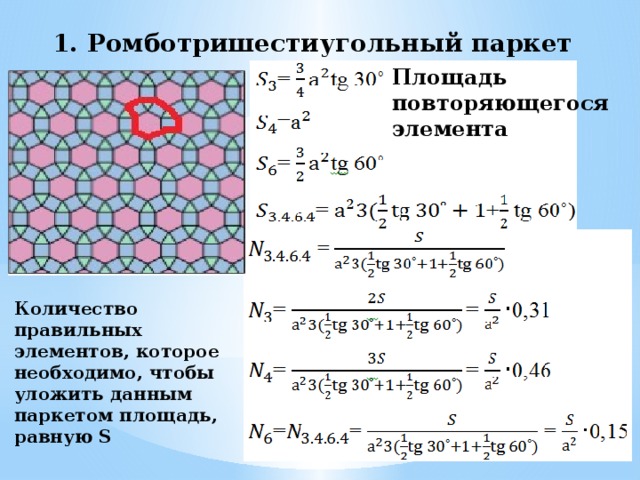
1. Ромботришестиугольный паркет 3.4.6.4

Площадь повторяющегося элемента

Количество правильных элементов, которое необходимо, чтобы уложить данным паркетом площадь, равную S

2. Курносый квадратный паркет 3.3.4.3.4.

Площадь повторяющегося элемента

Количество правильных элементов, которое необходимо, чтобы уложить данным паркетом площадь, равную S

3. Усечённый квадратный паркет 4.8.8

Площадь повторяющегося элемента

Количество правильных элементов, которое необходимо, чтобы уложить данным паркетом площадь, равную S

4. Тришестиугольный паркет 3.6.3.6

Площадь повторяющегося элемента

Количество правильных элементов, которое необходимо, чтобы уложить данным паркетом площадь, равную S

5. Усеченный шестиугольный паркет 3.12.12

Площадь повторяющегося элемента

Количество правильных элементов, которое необходимо, чтобы уложить данным паркетом площадь, равную S

6. Ромбоусеченный тришестиугольный паркет 4.6.12

7. Изокурносый треугольный паркет 3.3.3.4.4

8. Курносый тришестиугольный паркет 3.3.3.3.6

Заключение

В заключении подведем итоги. Мы рассмотрели 8 основных видов паркетов из правильных многоугольников и рассчитали для каждого из них зависимость количества различных повторяющихся элементов, как отдельных многоугольников, так и их укладок, от стороны a многоугольника, а также площади S , которую требуется замостить данным паркетом.

Таким образом, цели и задачи нашей работы были полностью достигнуты.