9
Оглавление
1.Задачи 2
1.1Ребусы: 2
1.2.Магические квадраты: 2
1.3. Логические задачи: 3
1.4. Комбинаторные задачи: 4
2. Ответы: 5
2.1. Ребусы 5
2.2.Магические квадраты: 6
2.3. Логические задачи: 6
2.4.Комбинаторные задачи: 8
1.Задачи 1.1Ребусы:
| 1 | 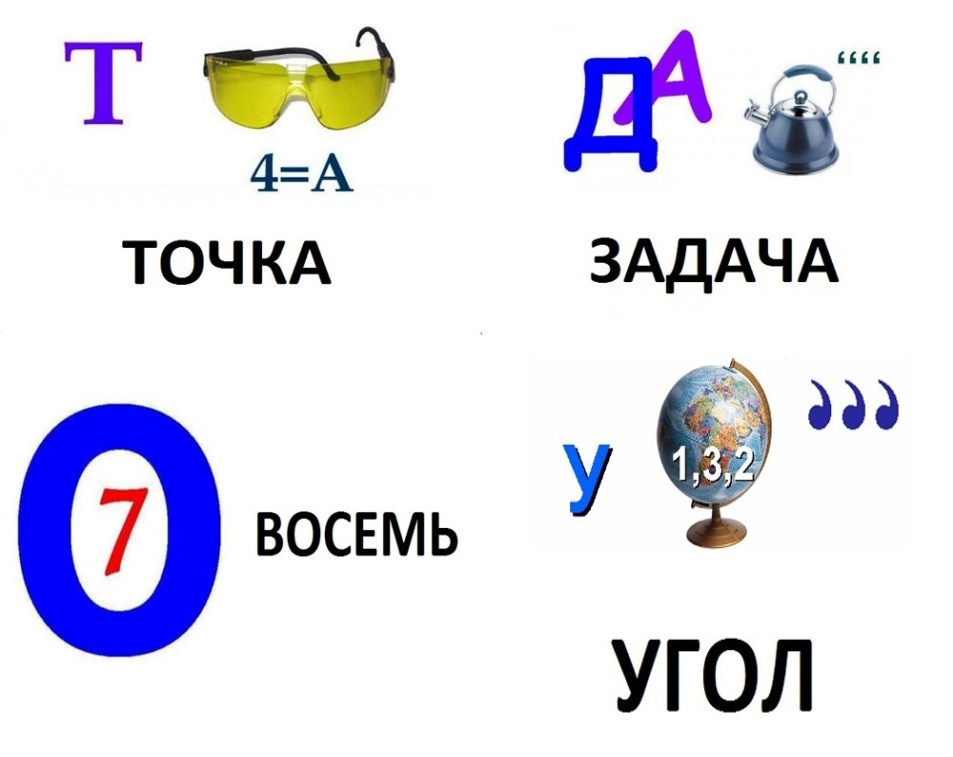
| 2 | 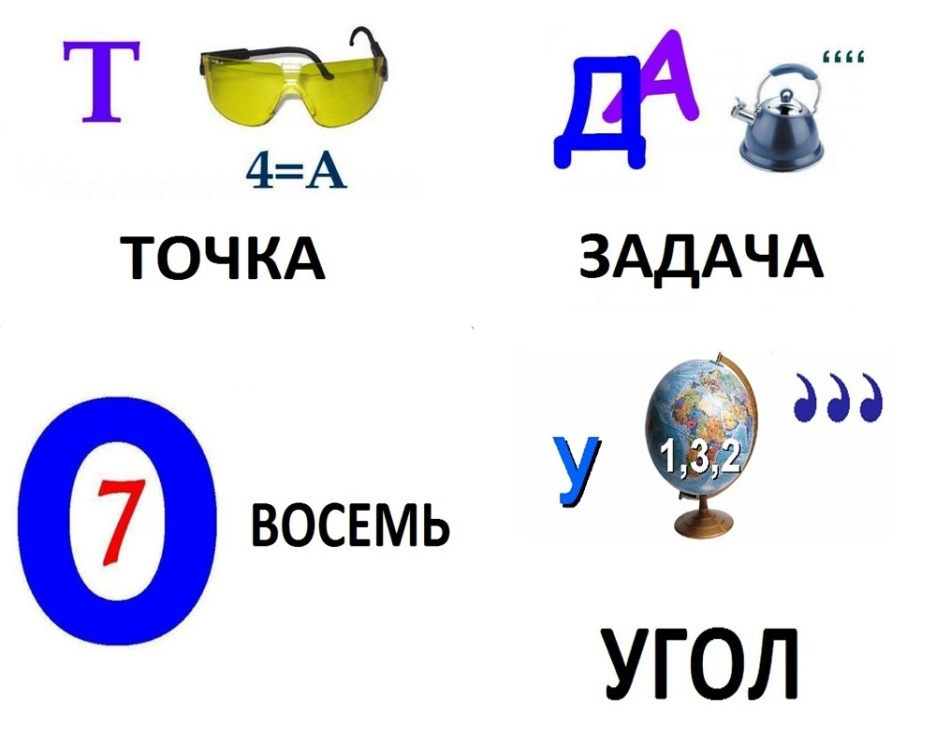
| 3 | 
|
| 4 | 
| 5 | 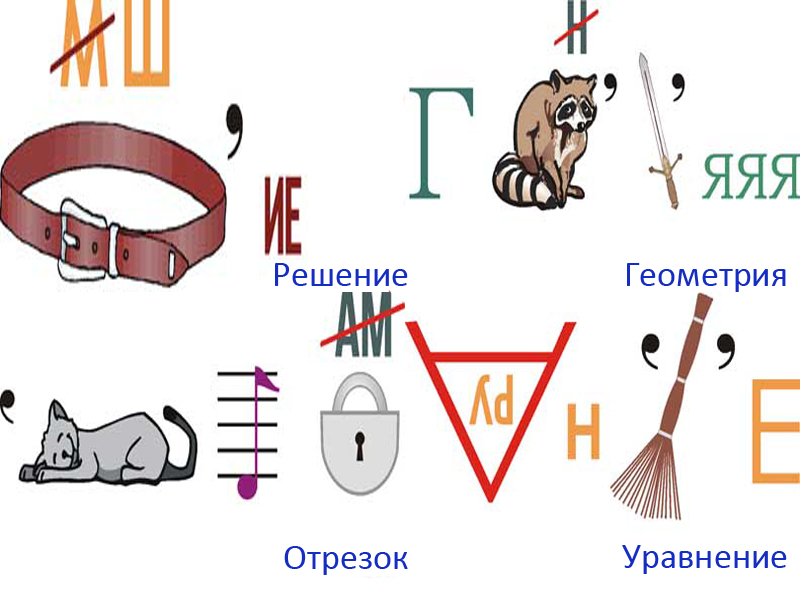
| 6 | 
|
| 7 | 
| 8 | 
| 9 | 
|
| 10 | 
| 11 | 
| 12 | 
|
| 13 | 
|
|
|
| 14 | 
|
|
|
1.2.Магические квадраты:
| 1 | 
| 2 | 
|
| 3 | 
| 4 | 
|
1.3. Логические задачи:
1)Кирпич весит 1 килограмм плюс половину собственного веса. Сколько весит кирпич?
2) Как умножать любое двухзначное число на 11?
3) Примерно за 40 секунд, не используя калькулятора, определите, что больше: 351х354 или 352х353.
4) Примерно за 10 секунд без подручных средств, чему равно выражение: (2/3) х (3/4) х (4/5) х (5/6) х (6/7)
5) Постарайтесь за 20 секунд определить, что больше:
А) 420/978 - 211/977
Б) 209/977
6) Междугородний автобус проехал расстояние между двумя городами со скоростью 60 км/ч. Обратный путь он проехал со скоростью 40 км/ч. Найдите среднюю скорость автобуса.
7) Как быстро сосчитать сумму чисел последовательности: 1 + 2 + 3 + ... + 99
8) Имеется две емкости, в одной трех процентный раствор спирта, в другой емкости тридцати процентный. В какой пропорции необходимо смешать обе жидкости, чтобы получить двенадцати процентный раствор?
9) Один рыбак поймал очень большую рыбу и решил узнать – сколько она весит целиком. Целиком рыба на весы не помещалась, поэтому он ее взвесил по частям: хвост весил 40кг, голова весила столько же, сколько хвост с половиной туловища, туловище весило столько же, сколько голова с хвостом. Сколько же весила рыба целиком?
10) Пассажир поезда, проехав половину пути, лег спать. Он спал до тех пор, пока не осталось ехать половину того пути, что он проехал спящим. Какую часть всего пути он проехал спящим? 11) На острове живут два племени: молодцы, которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник встретил островитянина, спросил его, кто он такой, и когда услышал, что он из племени молодцов, нанял его в проводники. Они пошли и увидели вдали другого островитянина, и путешественник послал своего проводника спросить его, к какому племени он принадлежит. Проводник вернулся и сказал, что тот утверждает, что он из племени молодцов. Спрашивается: был проводник молодцом или лгуном?
12) Пять землекопов за 5 часов выкапывают 5 м канавы. Сколько потребуется землекопов, для того чтобы выкопать 100 м канавы за 100 часов?
13) Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
14) Трехлитровый сосуд полностью заполнен тремя литрами воды. Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды. При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.
15) Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
16) Как вы думаете, если полста разделить на половину, то сколько в итоге получится?
17) Если три десятка умножить на четыре десятка, то сколько получится?
1.4. Комбинаторные задачи:
1)При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов?
2)В хоровом кружке занимаются 9 человек. Необходимо выбрать двух солистов. Сколькими способами это можно сделать?
3)Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях?
4)Пятеро друзей сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно?
5)В меню столовой предложено на выбор 2 первых блюда, 6 вторых и 4 третьих блюда. Сколько различных вариантов обеда, состоящего из первого, второго и третьего блюда, можно составить?
6)В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими разными способами можно выбрать покупку из одного блокнота и одной ручки?
7)На прививку в медпункт отправились 7 друзей. Сколькими разными способами они могут встать в очередь у медицинского кабинета?
8)Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются).
9)При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей?
10)В спортивной команде 9 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
2. Ответы: 2.1. Ребусы
Точка
Задача
Восемь
Угол
Решение
Геометрия
Отрезок
Уравнение
Равенство
Числитель
Знаменатель
Диагональ
Модуль
Квадрат
2.2.Магические квадраты:
2.3. Логические задачи:
1)Вам поможет обычное уравнение: 1 кирпич = 1кг + ½ кирпича, то есть x=1+x/2, откуда x-x/2=1, откуда 2x-x=2, откуда x=2, то есть кирпич весит 2кг.
2) Для того, чтобы умножать на 11 существует специальный метод, позволяющий совершать операции даже с очень большими множителями. Для начала продемонстрирую пример того, как можно умножить на 11 любое двузначное число.
Пример 42*11 решается просто. Пишем цифры «4» и «2», а между ними «4+2». Получается 462 – это и есть верный ответ. Если сумма в скобках больше 10, тогда пишем по центру количество единиц от суммы, а к первой цифре добавляем «1». Например:
93*11 = 9 (9+3) 3 = 1023
3) 352х353 больше, чем 351х354. Здесь минимум два варианта решения. Первый: всем известно, что площадь квадрата является максимально возможной из всех вариантов прямоугольников с одинаковой суммой сторон А и В. В данном примере, по аналогии, сумма чисел также равна в обоих случаях (352 + 353 = 351 + 354). При этом ближе "к сторонам квадрата" будет вторая пара чисел (352 и 353). Второй вариант решения: необходимо каждое из двух выражений поделить на 353х351 . Получим 354/353 и 352/351. Или 1+1/353 и 1+1/351 . Очевидно, что второе число больше.
4) (2/7). Необходимо сократить все одинаковые числа (в числителях и знаменателях).
5) Б) 209/977. Решение: если прибавить к каждому выражению 211/977, то получим: 420/978 и 420/977. Очевидно, что второе больше.
6) 48 км/ч. Решение: простое деление на два сумму скоростей 60 и 40 не дает правильный результат, т.к. время движения автобуса в одну и в другую сторону отличается. Обозначим среднюю скорость через "х", а расстояние между городами "у". Из условия задачи получим уравнение: (2у : х) = (у/69 + у/40). Делим обе части уравнения на "у", получим: (2/х) = (1/60 + 1/40), откуда х = 48.
7) Решение: если к данной последовательности прибавить последовательность обратную: 99 + 98 + 97 + ... + 1 . Очевидно, что получится 100 * 99 = 9900. Так как суммы последовательностей равны, то необходимо разделить пополам 9900. Получим = 4950.
8) 1 : 2. Решение: пусть для двенадцати процентной смеси требуется "х" 3%-го раствора и "у" 30%-го. Тогда в первой смеси содержится 0,03х грамм чистого спирта, а во второй 0,3у, в всего 0,03х + 0,3у. В результате получается (х + у) грамм раствора, в котором чистого спирта должно быть 0,12 * (х + у). Получится уравнение 0,03х + 0,3у = 0,12(х + у). Отсюда: х = 2у, иными словами, 3%-го раствора надо взять вдвое больше, чем 30%-го.
9) Рыба весила целиком 320кг. Хвост = 40кг, голова = 120 кг, туловище = 160кг.
10) Выигрыш составил 2500 рублей. Каждый получил по 500 рублей: первый = 100 + 400 (осталось 2000), второй = 200 + 300 (осталось 1500), третий = 300 + 200 (осталось 1000), четвертый = 400 + 100 (осталось 500), пятый = 500.
11) Пассажир поезда спал 2/3 от половины всего пути, следовательно, он спал на протяжении 1/3 всего пути.
12) На острове на данный вопрос никто не мог ответить ничего, кроме того, что он молодец. Так как проводник воспроизвел правильно этот единственно возможный ответ, то ясно, что он молодец.
13) Понадобятся те же пять землекопов, не больше. В самом деле, пять землекопов за 5 часов выкапывают 5 м канавы; значит, пять землекопов за 1 час вырыли бы 1 м канавы, а в 100 часов — 100 м.
14) Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1.
15) Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев. Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
16) Равноудаленносьтю всех точек обладает любая линя, лежащая на поверхности шара.
17) Получится не 25, как многие могут подумать, а 100. Так как если 50 разделить на 1/2, то это равносильно умножению на 2.
18) Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200.
2.4.Комбинаторные задачи:
Ответ: 3
Ответ: 36
Ответ: 720
Ответ: 10
Ответ: 48
Ответ: 28
Ответ: 5040
Ответ: 6
Ответ: 15
Ответ: 72






























