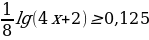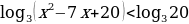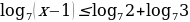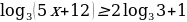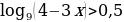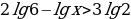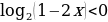Государственное бюджетное профессиональное образовательное учреждение «Саткинский медицинский техникум»
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
для обучающихся медицинских техникумов и колледжей
на тему: «Логарифмы»
ОДБ.05 Математика
Специальность 34.02.01 Сестринское дело
Сатка 2021
Учебно-методическое пособие для обучающихся медицинских техникумов и колледжей разработано в соответствии с требованиями Федерального Государственного образовательного стандарта по специальности 34.02.01 Сестринское дело
Организация–разработчик: ГБПОУ «Саткинский медицинский техникум»
Разработчик: Валеев Р.Ф. – преподаватель
Рассмотрена на заседании предметно-цикловой комиссии общих гуманитарных социально-экономических, общих профессиональных и естественнонаучных дисциплин.
Протокол №____от «____»_________________20___г. Председатель____________________Р.Ф. Дмитренко
Утверждена:
Зам.директора по УВР_________________А.Н.Гильмиярова
Оглавление
Пояснительная записка 4
Методические указания 4
Требования к результатам освоения дисциплины 5
1. Логарифм числа. 8
2. Функция y=logax, ее свойства. 13
3. Логарифмические неравенства 17
Список использованных источников 20
Пояснительная записка
Цель преподавания математики в ССУЗе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развивать логическое мышление и формировать математическую культуру; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.
Данное пособие предназначено для студентов 1-го курса специальности «Сестринское дело» для самостоятельной подготовки по теме «Логарифмы».
Методические указания
Уважаемые студенты вам предлагается поэтапное изучение темы «Логарифмы».
В каждом разделе предлагаются контрольные вопросы и задания, приводятся решения некоторых примеров и задач, а также приводятся задачи и упражнения, предназначенные для самостоятельной работы.
Выбор варианта производится соответственно номеру студента в списке группы.
Требования к результатам освоения дисциплины
• личностных:
- сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;
- понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
- готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
- готовность и способность к самостоятельной творческой и ответственной деятельности;
- готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
- отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;
• метапредметных:
- умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
- умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
- владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
- готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
- владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
- владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;
- целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;
• предметных:
- сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;
- сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
- владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;
- владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
- сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
- владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
- сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
- владение навыками использования готовых компьютерных программ при решении задач.
1. Логарифм числа.
1.1 Понятие логарифма.
Логарифмом положительного числа N по основанию а (а 0, а≠1) называется показатель степени х, в которую нужно возвести число а, чтобы получить число N, т.е.
logа N = х или ах = N.
Пример 1:
log 2 8 =?
Решение:
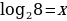
Идем от обратного:
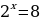
8 = 23
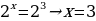
Ответ: log 2 8 =3
Пример 2:
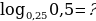
Решение:
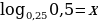
Идем от обратного:
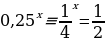
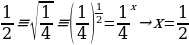
Ответ: 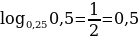
Пример 3:
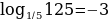 т.к. (1/5)-3 =125
т.к. (1/5)-3 =125
Пример 4:
log4 (1/64) = -4 т.к. 4-4 =1/64
Операцию нахождения логарифма числа называют логарифмированием. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием.
Вычисление значения логарифма сводится, как правило, к решению некоторого показательного уравнения.
Использование логарифма позволяет сводить умножение и деление чисел (представленных в виде степеней некоторого числа, принятого за основание) к сложению и вычитанию показателей степеней, а возведение в степень и извлечение корня – к умножению и делению на показатель степени, поэтому применение логарифмов упрощает и сокращает сложные вычисления.
-
Свойства логарифмов.
-
Логарифм единицы равен нулю.
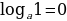
-
Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
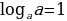
-
Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:
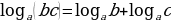
Например: 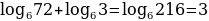
-
Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
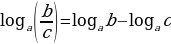
Например: 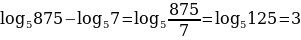
-
Если в основании и в аргументе логарифма стоят степени, показатели этих степеней можно вынести за знак логарифма:
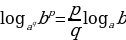
Например: 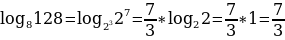
-
При работе с логарифмами можно перейти к новому основанию:
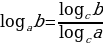
Данное свойство широко применятся при вычислении логарифмов при помощи калькулятора.
Например: 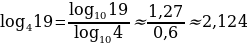
-
Можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе:
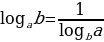
Например: 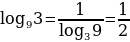
Если основанием логарифма является число е=2,71828…, то логарифм называется натуральным и обозначается lnx.
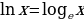
При нашей десятичной системе счисления самым удобным основанием является число 10.
Логарифм по основанию 10 называется десятичным логарифмом и обозначается lgx:
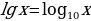
Вопросы для самоконтроля
-
Что называют логарифмом числа?
-
Что такое натуральный логарифм?
-
Что такое десятичный логарифм?
-
Перечислите свойства логарифмов?
Задания для самостоятельной работы.
Решите уравнения
Вариант 1.
а) 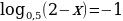 ;
;
б) 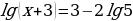 ;
;
в) 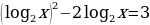 .
.
Вариант 2.
а) 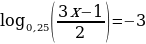 ;
;
б) 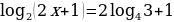 ;
;
в) 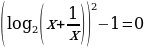 .
.
Вариант 3.
а) 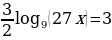 ;
;
б) 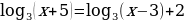 ;
;
в) 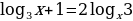 .
.
Вариант 4.
а) 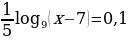 ;
;
б) 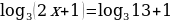 ;
;
в) 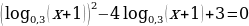 .
.
Вариант 5.
а)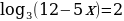 ;
;
б) 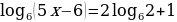 ;
;
в) 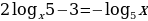 .
.
Вариант 6.
а) 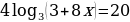 ;
;
б) 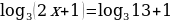 ;
;
в)  .
.
Вариант 7.
а) ;
;
б) 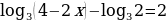 ;
;
в) 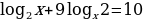 .
.
Вариант 8.
а) 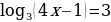 ;
;
б) 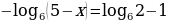 ;
;
в) 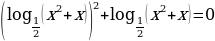 .
.
Вариант 9.
а)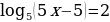 ;
;
б)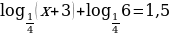 ;
;
в) 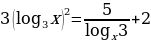 .
.
Вариант 10.
а) 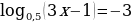 ;
;
б)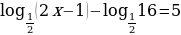 ;
;
в) 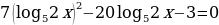 .
.
2. Функция y=log
ax, ее свойства.
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) - данная запись будет обозначать логарифм b по основанию а.
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x1, и отрицательной при 0(рис. 2.1).
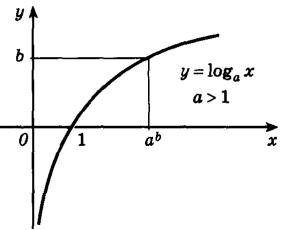
Рис. 2.1
Возрастающая логарифмическая функция
6. Убывающая логарифмическая функция, будет отрицательной при х1, и положительной при 0(рис. 2.2).
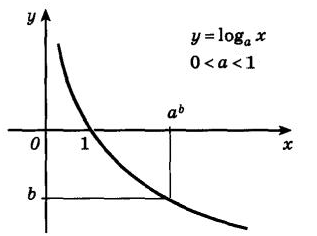
Рис. 2.2
Убывающая логарифмическая функция
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. (рис. 2.3).
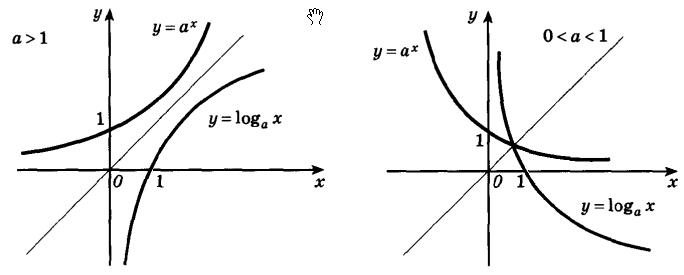
Рис. 2.3
Взаимное расположение графиков логарифмической и показательной функций
Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций.
Вопросы для самоконтроля
-
Что называют логарифмической функцией?
-
Чему равна область определения логарифмической функции?
-
Чему равна область значений логарифмической функции?
Задания для самостоятельной работы.
-
Найти область определения логарифмической функции
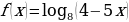 .
.
Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 - 5*x0. Решаем это неравенство и получаем x.
Таким образом, получается, что областью определения функции f(x) = log8(4 - 5*x) будет являться промежуток (-∞;0.8)
2. Найдите область определения функции 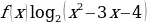 .
.
Как и в предыдущем примере, функция f определена для всех тех х, при которых 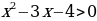 . Решая это квадратное неравенство, получаем что D(f) – объединение интервалов (-∞; -1) и (4;∞).
. Решая это квадратное неравенство, получаем что D(f) – объединение интервалов (-∞; -1) и (4;∞).
3. Найдите область определения функции.
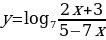 .
.
Найти:
D(y) -?
Решение:
Аргумент логарифмической функции всегда положителен, поэтому:
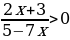
Если дробь положительна, то числитель и знаменатель имеют одинаковые знаки.
Решение производится методом интервалов.
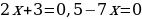
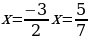
-
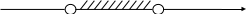 + -
+ -
-3/2 5/7
Ответ: 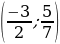 .
.
4. Найдите область определения следующих функций.
Вариант 1.
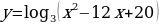
Вариант 2.
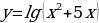
Вариант 3.
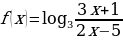
Вариант 4.
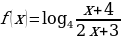
Вариант 5.
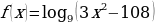
Вариант 6.
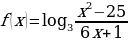
Вариант 7.
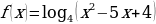
Вариант 8.
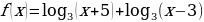
Вариант 9.
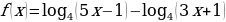
Вариант 10.
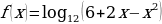
3. Логарифмические неравенства
Логарифмическим неравенством называется неравенство, в котором неизвестная величина стоит под знаком логарифма, т. е. неравенства вида:
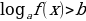

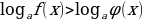
1 случай
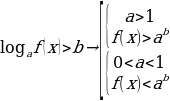
2 случай
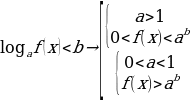
3 случай
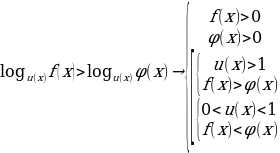
Задания для самоконтроля
1. Решить неравенство 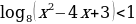
Решение:
Область определения данного неравенства будет определяться условием 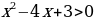 , основанием логарифма служит число 8. Т.к. знак неравенства «меньше», а основание больше 1, то при «избавлении» от знака логарифма, мы получим систему из 2 неравенств.
, основанием логарифма служит число 8. Т.к. знак неравенства «меньше», а основание больше 1, то при «избавлении» от знака логарифма, мы получим систему из 2 неравенств.
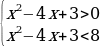
или
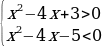
Решать данные неравентсва можно любым из известных способов.
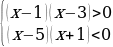
Решение верхнего неравенства
 + - +
+ - +
-
3
Решение нижнего неравенства
 + - +
+ - +
-1 5
Теперь накладываем друг на друга получившиеся промежутки
-1 1 3 5
Ответ: 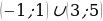 .
.
2. Решить неравенство:
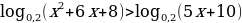
Решение:
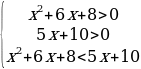
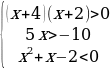
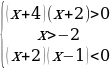
Решение верхнего неравенства
 + - +
+ - +
-4 -2
Решение среднего неравенства
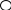
-2
Решение нижнего неравенства
 + - +
+ - +
-2 1
Теперь накладываем друг на друга получившиеся промежутки
 -4 -2 1
-4 -2 1
Ответ: 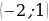 .
.
3. Решите неравенства
Вариант 1.
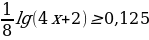
Вариант 2.
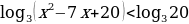
Вариант 3.
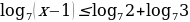
Вариант 4.
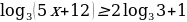
Вариант 5.
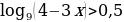
Вариант 6.
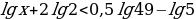
Вариант 7.
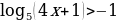
Вариант 8.
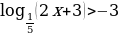
Вариант 9.
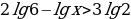
Вариант 10.
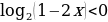
Список использованных источников
Основные источники:
-
Математика : алгебра и начала математического анализа; геометрия / Луканкин А. Г. - Москва : ГЭОТАР-Медиа, 2018. - 560 с. - ISBN 978-5-9704-4361-3. - Текст : электронный // URL : http://www.medcollegelib.ru/book/ISBN9785970443613.html
интернет-ресурсы
www.fcior.edu.ru (Информационные, тренировочные и контрольные материалы).
www.school-collection.edu.ru (Единая коллекции цифровых образовательных ресурсов).






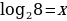
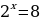
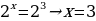
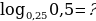
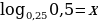
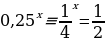
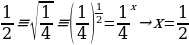
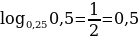
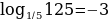 т.к. (1/5)-3 =125
т.к. (1/5)-3 =125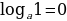
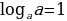
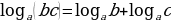
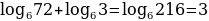
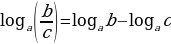
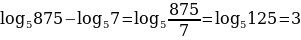
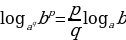
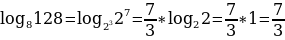
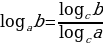
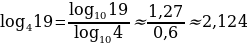
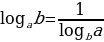
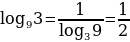
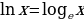
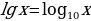
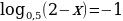 ;
;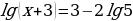 ;
;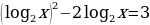 .
.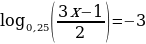 ;
;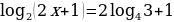 ;
;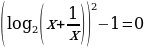 .
.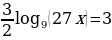 ;
;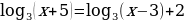 ;
;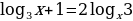 .
.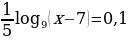 ;
;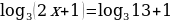 ;
;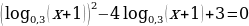 .
.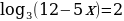 ;
;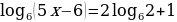 ;
;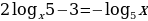 .
.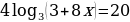 ;
; .
. ;
;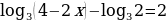 ;
;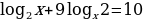 .
.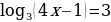 ;
;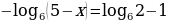 ;
;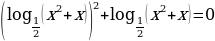 .
.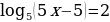 ;
;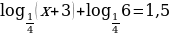 ;
;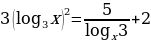 .
.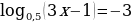 ;
;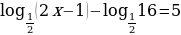 ;
;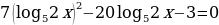 .
.


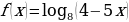 .
.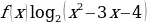 .
.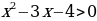 . Решая это квадратное неравенство, получаем что D(f) – объединение интервалов (-∞; -1) и (4;∞).
. Решая это квадратное неравенство, получаем что D(f) – объединение интервалов (-∞; -1) и (4;∞).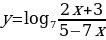 .
.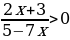
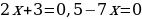
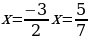
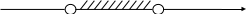 + -
+ - .
.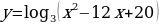
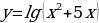
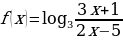
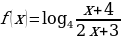
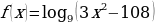
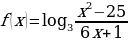
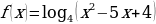
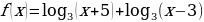
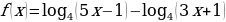
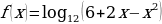
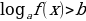

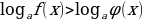
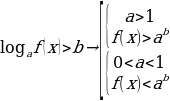
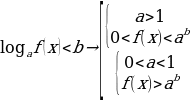
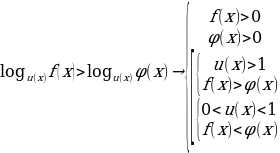
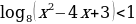
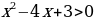 , основанием логарифма служит число 8. Т.к. знак неравенства «меньше», а основание больше 1, то при «избавлении» от знака логарифма, мы получим систему из 2 неравенств.
, основанием логарифма служит число 8. Т.к. знак неравенства «меньше», а основание больше 1, то при «избавлении» от знака логарифма, мы получим систему из 2 неравенств.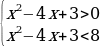
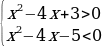
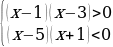
 + - +
+ - + + - +
+ - +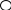
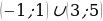 .
.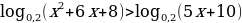
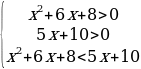
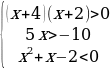
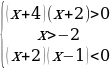
 -4 -2 1
-4 -2 1 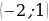 .
.