муниципальное образовательное учреждение
гимназия имени А.Л.Кекина
города Ростова Великого
УЧЕБНЫЙ ПРОЕКТ
ПО МАТЕМАТИКЕ
РАЗДЕЛ: АЛГЕБРА
НА ТЕМУ:
«КРИПТОГРАФИЯ В МАТЕМАТИКЕ»
Выполнила ученица
9 класса «В»
Миронова Виктория
Ростов
2019
Оглавление:
1.Введение стр. 3
2.Основная часть стр. 4
3.Заключение стр. 8
4.Список используемой литературы стр. 9
2
Сегодня ни один образованный человек не может обойтись без информации и передачи ее другим людям. Мы общаемся, обмениваемся данными в основном с помощью мобильных устройств, телефонов, смартфонов и других гаджетов. Нам не приходится думать, что послание, переданное другому человеку, защищено и надежно спрятано от не желательных читателей. Что позволяет скрыть нужную информацию от посторонних и передать ее нужному адресату, втайне от других?
Криптография – наука о шифрах. Долгое время она была засекречена, так как применялась, в основном, для защиты государственных и военных секретов. Современная криптография бурно развивается. В ней появляются новые направления. Наряду с термином «криптография» встречается термин «криптология». Он используется для обозначения всей области секретной связи. Криптография – прикладная наука, она использует самые последние достижения фундаментальных наук и, в первую очередь, математики.
Методы и результаты различных разделов математики (в частности, алгебры, теории чисел, теории алгоритмов, теории вероятностей и математической статистики) используются как при разработке шифров, так и при их исследованиях, в частности, при поиске методов вскрытия шифров.
Геометрия оказала определенное влияние на криптографию. Для защиты информации многие виды шифров представлены в виде геометрических фигур.
| Геометрическая фигура | Наименование шифра |
| Отрезок | Шифры Цезаря(фильм), линейка Энея |
| Цилиндр (конус) | Шифр Сцитала(2) |
| Круг | Диск Альберти(3) |
| Треугольник | Шифр Уилкинса |
| Квадрат | «Магический квадрат» Квадрат Полибия |
| Прямоугольник | Шифр перестановки по группам Шифр Чейза(4) |
1  2
2 
![]()
3  4
4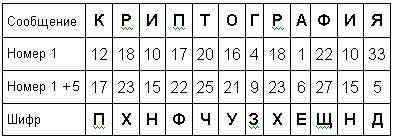
3
Из вышеперечисленных видов шифра больше всего меня заинтересовал диск Альберти, и я хочу поподробней про него рассказать.
«Диск Альберти» состоял из двух дисков — внешнего неподвижного (на нём были нанесены латинские буквы в алфавитном порядке и цифры 1, 2, 3, 4) и подвижного внутреннего диска, на котором буквы были переставлены. Диски крепились на одной оси так, чтобы внутренний мог вращаться. Окружность каждого диска разделена на 24 равные клетки. Скольжение алфавитов находится под контролем ключевых букв, включённых в тело криптограммы. Для того, чтобы расшифровать сообщение, написанное с использованием дисков Альберти вы должны были иметь соответствующий алфавит на ваш внутренний диск.
Принцип построения этого шифра заключается в следующем: для шифрования используются не один как в простой замене, а несколько шифралфавитов. Процесс шифрования заключался в нахождении буквы открытого текста на внешнем диске и замене её на букву с внутреннего диска, стоящую под ней. После этого внутренний диск сдвигался на одну позицию и шифрование второй буквы производилось уже по новому шифралфавиту. Ключом данного шифра являлся порядок расположения букв на внутреннем диске и его начальное положение относительно внешнего диска. Другим изобретением Альберти стали коды, он предложил заменять на упорядоченные двух-, трёх- и четырёх цифровые комбинации слоги, слова и целые предложения (всего таких комбинаций 336). После этого цифры перешифровывались многоалфавитной заменой. Как видим, диск — механическое устройство для осуществления простой замены. Изобретение такого устройства ещё не поясняет, почему Альберти признают отцом западноевропейской криптологии. Главная заслуга Альберти — использование не одного, а нескольких алфавитов, что затрудняет частотный анализ. Переключение с одного на другой алфавит Альберти предлагал делать через каждые 3-4 слова. Это делается поворотом внутреннего диска в ту или другую сторону на определённое число делений. Сигналом такого переключения служила заглавная буква. Без этой причины заглавные буквы в тексте не имели места быть. Сначала Альберти использовал два алфавита, потом больше. Таким образом, Альберти одним из первых выдвинул идею «двойного шифрования» — текст, полученный в результате первого шифрования, подвергался повторному шифрованию другим шифром. Идеи Альберти использовались при создании шифрмашин в первой половине XX века, некоторые из них использовались в разных странах до 1980-х годов.

4
Каждый может составить собственный шифр, кто-то сложнее, кто-то проще, придумав просто любые обозначения для каждой буквы алфавита. Примером могут служить такие шифры-полуфабрикаты:
Расшифруем послание:
| ø | А | µ | К | ¿ | Х |
| Ŧ | Б | ¢ | Л | Đ | Ц |
| ∫ | В | ð | М | × | Ч |
| ℓ | Г | ¤ | Н | Ŀ | Ш |
| ∑ | Д | ¶ | О | ſ | Щ |
| ∂ | Е | Ξ | П | ς | Ъ |
| √ | Ё | Ł | Р | ґ | Ы |
| ‡ | Ж | ł | С | џ | Ь |
| † | З | λ | Т | ћ | Э |
| ψ | И | δ | У | ≈ | Ю |
| φ | Й | ξ | Ф | θ | Я |
1. ðøλ∂ðøλψµø - ћλ¶ Ŧ¶¢џĿ∂ ×∂ð ¤øδµø, ћλ¶ θ†ґµ ¤øδµψ.
2. łλŁ¶ℓ¶łλџ ∫ ðøλ∂ðøλψµ∂ ¶†¤ø×ø∂λ, ΞŁ∂‡∑∂ ∫ł∂ℓ¶, ∑¶ŦŁ¶ł¶∫∂łλ¤¶łλџ ψ θł¤¶łλџ.
3. «¶×∂∫ψ∑¤ґφ» - łøð¶∂ ¶Ξøł¤¶∂ ł¢¶∫¶ ∫ ðøλ∂ðøλψµ∂.
4. ðøλ∂ðøλψµø - µ¶Ł¶¢∂∫ø ψ ł¢δ‡ø¤µø ¤øδµ.
5. ðøλ∂ðøλψµø ∑¢θ δ×√¤¶ℓ¶, λ¶ ‡∂ łøð¶∂, ×λ¶ łµø¢џΞ∂¢џ ∑¢θ ø¤øλ¶ðø.
1. Математика – это больше чем наука, это язык науки.
Нильс Бор
2. Строгость в математике означает, прежде всего, добросовестность и ясность.
Липман Берс
3. «Очевидный» – самое опасное слово в математике.
Эрик Темпл Белл
4. Математика – королева и служанка наук.
Эрик Темпл Белл
5. Математика для учёного – то же самое, что скальпель для анатома.
Нильс Абель
5
Решив не отставать от учёных, я придумала свой шифр. Он называется verschlüsseln, что в переводе с немецкого означает- зашифрованный.

Для составления шифра я использовала учебник математики 5 класса (Н.Я. Виленкин; В.И. Жохов 2009 год), учебник по алгебре 7 класса (Ю.Н. Макарычев; Н.Г Миндюк 2014 год), учебник математики 8 класса (Г.В. Дорофеев; С.Б. Суворова 2007 год) и теорию по геометрии и алгебре за 9 класс.
Если составлять такой шифр, можно пользоваться любыми источниками информации: учебники, энциклопедии, интернет-ресурсы. Можно придумать любую фигуру и разделить её под цифры по своему вкусу.
Суть шифра заключается в том, что для каждой цифры соответствует одно или несколько слов. Шифр можно разгадать 2 способами.
а)Собирая цепочку из цифр: нужно 1)написать термин о котором идёт речь 2)закончить предложение 3) написать условия 4)решить уравнение (оно включено в 21)
б)Выписать все слова и собрать предложения по смыслу
Цифры в нескольких предложениях могут повторяться.
Для начала ознакомимся со словами, принадлежащими той или иной цифре:
1-без
2-называют
3-графиком
4-синус
5-при
6-линейной
7-площади треугольника
8-периметр
9-косинус
10-функции
11-перестановке
12-десять
13-многоугольник
14-сантиметров
15-нарушение
16-если
17-симметрии
18-аксиома
19-это отношение
20-y=kx
21-x3 -5x2-6x=0
22-площади круга
23-правльным
24-сто
25-биссектриса угла
26-точки
27-принимаемое
28-формула
29-сумма
30-это
31-площади трапеции
32-y=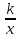
33-процент
34-вторая
35-цифры
36-слагаемых
37-знаки для
38-координата
39-утверждение
40-является
41-площади квадрата
6
Пример шифровок:
1) 24 14 2 сто сантиметров называют ….. дальше надо продолжить предложение -метром
2) 12 14 2 десять сантиметров называют - дециметром
3) 5 11 36 29 при перестановке слагаемых сумма - не меняется
4) 28 41 формула площади квадрата S=a2
5) 3 6 10 40 графиком линейной функции является - прямая
6) 4 19 синус это отношение - противолежащего катета к гипотенузе
7) 9 19 косинус это отношение - прилежащего катета к гипотенузе
8) 8 30 периметр это - сумма всех сторон геометрической фигуры
9) 13 2 23 16 многоугольник называют правильным если 1)все стороны равны
2)все углы равны
10) 21 решите уравнение x3-5x2-6x=0
x(x2-5x-6)=0
x=0 или x2-5x-6=0
x1=-1
x2=6
Ответ: 1; 0; 6.
11) 15 17 нарушение симметрии - асимметрия
12) 3 10 20 40 графиком функции y = kx является - прямая, проходящая через начало координат
13) 3 10 32 40 графиком функции y = 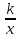 является - гипербола
является - гипербола
14) 28 7 формула площади треугольника - S= ah
ah
15) 28 31 формула площади трапеции - S=  h
h
16) 33 30 процент это - сотая часть числа
17) 35 30 37 цифры это знаки для - обозначения чисел
18) 18 39 27 1 аксиома утверждение принимаемое без - доказательств
19) 25 30 биссектриса угла это - луч, делящий угол пополам
20) 34 38 26 вторая координата точки - ордината
21) 28 22 формула площади круга - S= 2
2
С помощью такого шифра можно зашифровывать тайные послания и передавать информацию.
Понимание математического характера криптографии началось с работ все того же К. Шеннона. Его труд «Математическая теория криптографии» в секретном варианте появился в 1945 году. А рассекречен и опубликован был в США в 1949 году. В 1963 году по инициативе А. Н. Колмогорова сборник работ К. Шеннона был издан и на русском языке.

Криптографические методы и средства защиты информации, а также их математические основы являются фундаментальными исследованиями, связывающими воедино области математики, информатики и физики. Одним из разделов математики, который используется в криптографии, является комбинаторика. Она занимается разного рода наборами, которые можно образовывать из элементов некоего конечного множества.
7
Некоторые элементы комбинаторики были известны в Индии ещё во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют «сочетаниями».
В XII в. Баскара вычислял некоторые виды сочетаний и перестановок. Как научная дисциплина комбинаторика сформировалась в XVII в. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1665 г. работы 16 «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок.

Изучением размещений впервые занимался Я. Бернулли во второй части своей книги «Ars conjectandi» («Искусство предугадывания») в 1713 г.

Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в. Для криптографии важными являются такие алгоритмы комбинаторики как правило умножения, выборки и перестановки. На этих алгоритмах основываются способы формирования секретных ключей для симметричных шифров. Криптосистемы разделяются на симметричные и с открытым ключом (ассиметричные). В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ. В системах с открытым ключом используются два ключа - открытый и закрытый, которые математически связаны друг с другом. Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается с помощью закрытого ключа, известного только получателю сообщения.
Вывод:
Значение криптографии в математике имеет большую роль. С помощью неё передача секретной информации стала намного проще. Свой шифр может составить абсолютно каждый человек для своих целей. Специфика криптографии состоит в том, что она направлена на разработку методов, обеспечивающих стойкость к любым действиям злоумышленника, в то время как на момент криптосистемы невозможно предусмотреть все способы атаки, которые могут, изобретены в будущем на основе новых достижений теории и технологического прогресса.
Несомненно, криптография будет развиваться дальше весьма активно. Одна из её задач на будущее - разработка скоростных методов шифрования с высоким уровнем секретности. Эта задача обусловлена большим количеством каналов связи (беспроводные сети, сотовая связь), по которым передаются очень большие объёмы информации.
8
Источники:
учебник по математике 5 и 8 класс
учебник по алгебре 7 класс
Демпан И.Я.; Виленкин Н.Я.За страницами учебника математики: Пособие для учащихся 5-6 кл.сред.шк.- М.: Просвещение, 1989.-287с.
Информационный ресурс - http/moluch.ru/conf/tech/archive/163/8782/
Информационный ресурс - https://ru wikipidia
Соболева. Т.А. История информационного дела в России.- М.: 1994
Ященко В. В. Введение в криптографию
Баричев С.Г. Основы современной криптологии - М.: 2001
Информационный ресурс - htt://www.intuit.ru/studies/courses/
9







 2
2 
 4
4


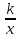


 2
2