Учебный проект. Тригонометрическая подстановка.

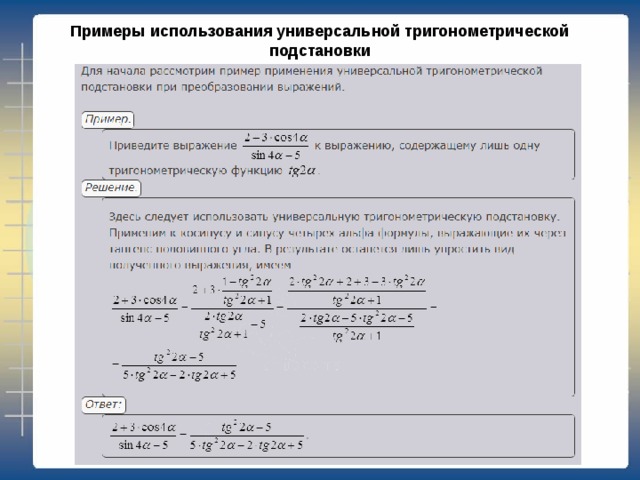
Примеры использования универсальной тригонометрической подстановки

ТРИГОНОМЕТРИЧЕСКОЙ ПОДСТАНОВКИ ПРИ РЕШЕНИИ ЗАДАЧ

• Решение уравнений:
• А) Иррациональные уравнения
• Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. Эквивалентность не нарушается при возведении обеих частей в нечетную степень. В противном случае требуется проверка найденных решений или оценка знака обеих частей уравнения. Но существуют и другие приемы, которые могут оказаться более эффективными при решении иррациональных уравнений. Например, метод тригонометрической подстановки.

Б) Рациональные уравнения

• Тригонометрическая подстановка применяется при решении рациональных уравнений, когда уравнение не имеет рациональных корней или найденные рациональные решения не исчерпывают всего множества решений уравнения.
• При решении иррациональных уравнений возможность введения тригонометрической подстановки была видна по структуре уравнения. В нескольких следующих задачах применение метода тригонометрической подстановки не так очевидно. Вот почему прежде чем ввести подстановку, нужно доказать законность такого введения.

2)Решение систем:

Формулы тригонометрической подстановки

Рекуррентные последовательности

• Последовательность  u 1 ,  u 2 , …,  u n , … элементов поля  P  принято называть  рекуррентной (возвратной) последовательностью  порядка  k , если её члены удовлетворяют равенству (рекуррентному соотношению) Здесь n  принимает значения во множестве N натуральных чисел.

• где  k  – фиксированное натуральное число, называемое  порядком рекуррентности,   C i   – фиксированные элементы поля  P , называемые коэффициентами рекуррентного соотношения,  f ( n ) – некоторая функция, натурального аргумента͵ принимающая значения в поле  Р .

Последовательность { u n }, члены которой удовлетворяют соотношению (1), принято называть решением соотношения (1). Рассмотрим примеры рекуррентных последовательностей над полем  R  действительных чисел.

Пример 1: Последовательность Фибоначчи

• Последовательность Фибоначчи, ставшая известной большинству благодаря фильму и книге «Код да Винчи», это ряд чисел, выведенный итальянским математиком Пизанским Леонардо, более известным под псевдонимом Фибоначчи, в тринадцатом веке. Последователи ученого заметили, что формула, которой подчинен данный ряд цифр, находит свое отображение в окружающем нас мире и перекликается с другими математическими открытиями, тем самым открывая для нас дверь в тайны мироздания. В этой статье мы расскажем, что такое последовательность Фибоначчи, рассмотрим примеры отображения этой закономерности в природе, а также сравним с другими математическими теориями.

• Ряд Фибоначчи – это математическая последовательность, каждый элемент которой равен сумме двух предыдущих. Обозначим некий член последовательности как хn. Таким образом, получим формулу, справедливую для всего ряда: х n +2 =х n +х n +1. При этом порядок последовательности будет выглядеть так: 1, 1, 2, 3, 5, 8, 13, 21, 34. Следующим числом будет 55, так как сумма 21 и 34 равна 55. И так далее по такому же принципу.

Пример 2:

Геометрическая прогрессия - рекуррентная последовательность первого порядка, её члены удовлетворяют соотношению  b n +1  =  qb n ,  q  - знаменатель прогрессии.

Пример 3:

• Арифметическая прогрессия - рекуррентная последовательность первого порядка:  a n +1  =  a n  +  d ,  d  - разность прогрессии.
• Определœение. Рекуррентная последовательность { u n } принято называть  однородной  порядка  k  ( k  Î N), если её члены удовлетворяют соотношению:
• u n+k + С 1  u n+k-1  +…+ С k  u n  =0
• где  С i  - произвольные постоянные из поля  Р .
• Свойство 1 . Сумма решений рекуррентного соотношения является решением соотношения.
• Свойство 2 . Произведение решения рекуррентного соотношения на элемент поля  Р  является решением соотношения.
• Следствие. Множество решений соотношения относительно операций сложения решений и умножения решений на скаляры из поля  Р  образует векторное пространство над полем  Р .
• Определœение. Система последовательностей { a n 1 }, { a n 2 }, …, { a n s }, заданных в поле  Р , принято называть  линœейно независимой , если из тождеств относительно  n :
• a 1  a n 1  + a 2   a n 2  + … +  a s  a n s  = 0,  a i  - скаляры из  Р ,
• следует, что  a 1  =  a 2  = … =  a s  = 0.
• Найдем частное решение соотношения в виде геометрической прогрессии  l n . Подставим в данное решение. Получим уравнение относительно  l , называемое характеристическим уравнением
• l k  +  C 1 l k -1  + … +  C k  = 0
• данного рекуррентного соотношения. Это уравнение имеет не более  k  корней над полем  Р . Пусть  l 1 ,  l 2 , …,  l k  – корни характеристического уравнения.

Задачи:

• Первое условие означает, что число посередине равно среднему арифметическому двух других: 8 sinxcot2x=cosx−sinx8sin⁡xcot⁡2x=cos⁡x−sin⁡x. Удвоенная разность прогрессии равна 2 d=cosx+sinx2d=cos⁡x+sin⁡x, поэтому  cosx=a1+(k+1)dcos⁡x=a1+(k+1)d, и седьмой член равен 15= a7=cosx+(5−k)d=cosx+5−k2(cosx+sinx)=7−k2cosx+5−k2sinx15=a7=cos⁡x+(5−k)d=cos⁡x+5−k2(cos⁡x+sin⁡x)=7−k2cos⁡x+5−k2sin⁡x.
• Решая первое уравнение, имеем  cosx−sinx=8sinxcos2x2sinxcosx=4cos2xcosx=4(cosx−sinx)(cosx+sinx)cosxcos⁡x−sin⁡x=8sin⁡xcos⁡2x2sin⁡xcos⁡x=4cos⁡2xcos⁡x=4(cos⁡x−sin⁡x)(cos⁡x+sin⁡x)cos⁡x, где  cosx≠0cos⁡x≠0, sinx≠0sin⁡x≠0. Получается, что или  cosx=sinxcos⁡x=sin⁡x, или  cosx=4cosx+4sinxcos⁡x=4cos⁡x+4sin⁡x, то есть 3 cosx+4sinx=03cos⁡x+4sin⁡x=0.
• В первом случае оказывается, что 15=(6− k)cosx15=(6−k)cos⁡x, где  cosx=±12√cos⁡x=±12, что невозможно ввиду целочисленности  kk  и иррациональности 2–√2.
• Второй случай даёт два подслучая:  cosx=45cos⁡x=45, sinx=−35sin⁡x=−35, чему соответствует  k=11k=11, или  cosx=−45cos⁡x=−45, sinx=35sin⁡x=35, чему соответствует  k=15k=15. Ответ после этого легко выписать.

Заключение

• Изучение тригонометрических уравнений позволяет учащимся овладеть конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, развития умственных способностей, умение извлекать учебную информацию на основе сопоставительного анализа графиков, самостоятельно выполнять различные творческие работы.
• В данной работе рассмотрены основные методы решения тригонометрических уравнений, причем, как специфические, характерные только для тригонометрических уравнений, так и общие функциональные методы решения уравнений, применительно к тригонометрическим уравнениям.
• Для успешного решения уравнений необходимо знать формулы корней простейших тригонометрических уравнений, значение тригонометрических функций для основных углов и значение обратных тригонометрических функций, универсальные правила решения уравнений. Рассмотрено решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Указано, что при решении тригонометрических уравнений широко используются тождества, выражающие соотношение между тригонометрическими функциями одного и разных аргументов.

Источники информации:

• Алексеев А. Тригонометрические подстановки. // Квант. – 1995. - №2. –с. 40 – 42.
• Вавилов В. В. Задачи по математике. Алгебра / В. В. Вавилов, И. И. Мельников, С. Н. Олехник, П. И. Пасиченко. – М.: Наука, 1988. – С. 439
• Горнштейн П. И. Тригонометрия помогает алгебре / П. И. Горнштейн. – М.: Бюро Квантум, 1995. – С. 100-103. – Приложение к ж. «Квант», №3/95.
• Колягин Ю. М. Задачи в обучении математике / Ю. М. Колягин. – М.: Просвещение, 1977. – С. 143.
• Олехник С. Н. Нестандартные методы решения уравнений и неравенств: Справочник / С. Н. Олехник, М. К. Потапов, П. И. Пасиченко. – М.: Изд-во МГУ, 1991. – С. 143.
• Потапов М. К. Математика. Методы решения задач. Для поступающих в вузы: Учебное пособие / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. – М.: Дрофа, 1995. – С. 336.
• Фридман Л. И. Как научиться решать задачи / Л. И. Фридман, Е. Н. Турецкий. – М.: Московский психолого-социальный институт, 1999. – С. 240.
• Шарыгин И. Ф. Математика для школьников старших классов / И. Ф. Шарыгин. – М.: Дрофа, 1995. – С. 486.