Учебный проект "Удивительный мир правильных многогранников"

МКОУ «Торбеевская основная общеобразовательная школа имени А.И.Данилова»

Удивительный мир

правильных

многогранников

УЧЕБНЫЙ ПРОЕКТ

ученика 6 класса

Кошмелюка Ильи

Руководитель: Жарикова Л.С., учитель математики

Цель работы :

изучить правильные многогранники

и научиться делать их модели.

Задачи :

• найти и изучить в научно-популярной литературе и

в Интернете информацию о многогранниках;

• изготовить 5-6 моделей многогранников разными

способами;

• познакомить одноклассников со своими работами.

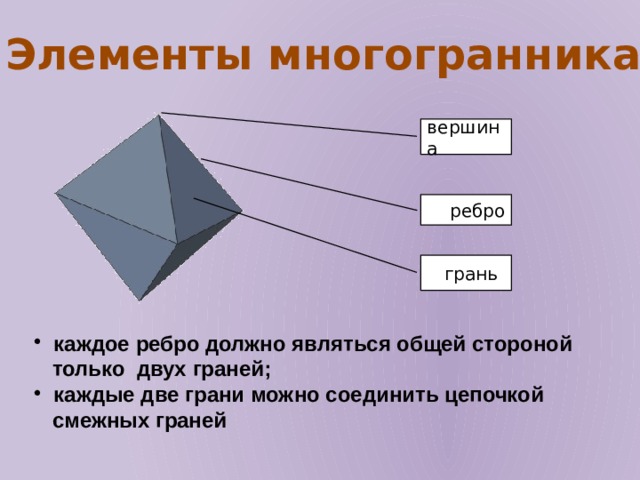
Элементы многогранника

вершина

ребро

грань

• каждое ребро должно являться общей стороной

только двух граней;

• каждые две грани можно соединить цепочкой

смежных граней

Формула Эйлера

В + Г = Р +2

или

В + Г – Р = 2,

где В – число вершин,

Г - число граней,

Р – число ребер

Правильные многогранники

Многогранник называется правильным, если:

• он выпуклый;
• все его грани являются равными правильными

многоугольниками;

• в каждой его вершине сходится одинаковое число

граней;

• все его двухгранные углы равны.

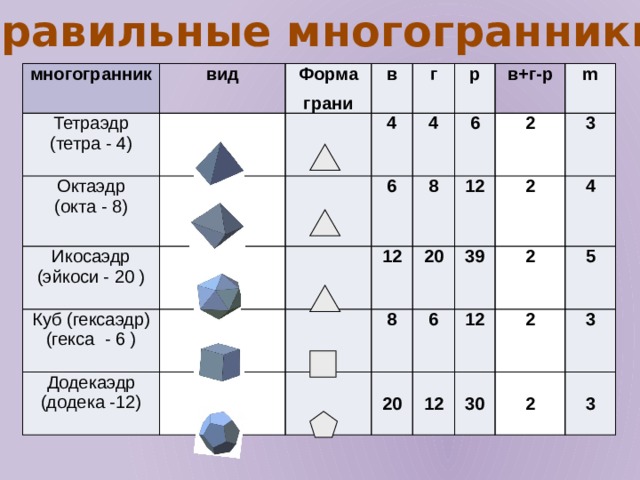
Правильные многогранники

многогранник

Тетраэдр

вид

Форма

(тетра - 4)

Октаэдр

грани

в

(окта - 8)

Икосаэдр

г

4

Куб (гексаэдр)

(эйкоси - 20 )

р

4

(гекса - 6 )

6

Додекаэдр

6

в+г-р

8

12

(додека -12)

2

m

12

20

8

3

20

39

2

6

12

2

4

12

2

5

30

2

3

3

Тетраэдр символизирует огонь, т.к. его вершина устремлена вверх; икосаэдр – воду, т.к. он самый «обтекаемый»; куб – землю, как самый «устойчивый»; октаэдр – воздух, как самый «воздушный». Пятый многогранник, додекаэдр, воплощал в себе «все сущее», символизировал все мироздание, считался главным.

Полуправильные многогранники

грани – правильные многоугольники,

но c разным количеством сторон

Ромбокубооктаэдр

в каждой вершине сходятся

• 4-угольные грани и

1 3-угольная

Усечённый октаэдр

в каждой вершине сходятся

2 6-угольные грани и

1 4-угольная.

Звёздчатые многогранники

у них в вершинах сходится разное количество граней .

звёздчатый икосаэдр

Грани – правильные треугольники,

во внутренних вершинах

сходится 5 треугольников,

а во внешних - 6.

звёздчатый октаэдр .

Грани – правильные треугольники,

во внутренних «вершинах» сходится 8 треугольников,

а во внешних -3.

Изготовление

моделей многогранников

Интересно разглядывать фотографии или модели многогранников, интересно читать о них, но всё-таки интереснее всего их делать своими руками

Способ 1. Склеивание из развёртки

додекаэдр

звёздчатый октаэдр

усечённый октаэдр

звёздчатый икосаэдр

Способ 2. Конструирование из трубочек

тетраэдр

октаэдр

Способ 3. Плетение

Плетение гексаэдра

Плетение тетраэдра

Способ 4. Оригами

додекаэдр

Способ 5. Соединение резиновыми колечками

Многогранники в природе

скелет феодарии

и вирус гепатита В

кристаллы соли ,

сернистого колчедана,

драгоценные камни

Многогранники в архитектуре

Моя коллекция

В основе красоты многогранников лежат

точные расчёты и строгая геометрия

Не зная математики, нельзя сделать

ничего прочного и прекрасного

Источники

• Веннинджер М. Модели многогранников. – М.:

Мир, 1974.

• Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная

геометрия. 5 – 6 кл.: Пособие для

общеобразовательных учебных заведений. – М.:

Дрофа, 1999.

• Математика. Еженедельная учебно-методическая

газета. №24, 2004.с. 15-32.

• Сайт: http : //polyhedron2008 . narod.ru