Учебно исследовательская работа «Определение высоты предмета различными способами (на примере памятника Петру I)»

Областная учебно-исследовательская конференция

«Юность Поморья»

Направление: Математика

«Определение высоты предмета различными способами

(на примере памятника Петру I)»

Работу выполнила:

Долинкина Ольга Сергеевна,

ученица 9 б класса,

МОУ ОГ №21 г. Архангельска.

Научный руководитель:

Трошина Елена Юрьевна,

учитель математики,

высшая квалификационная

категория,

МОУ ОГ №21 г. Архангельска.

г. Архангельск, 2010

Оглавление

Введение

На уроках геометрии, изучая тему «Измерительные работы на местности», мы вычисляли высоту предметов. В учебнике описаны некоторые методы решения задач на эту тему, но в них исходные данные определены. Нас же заинтересовало, а как на практике выполнить замеры, чтоб определить высоту объекта, и на сколько точным окажется результат вычислений. Для объекта исследования мы выбрали памятник Петру I, (высота которого известна – 7,2 м.)

Актуальность проблемы:

Компаниям сотовой связи для обеспечения качественной беспроводной передачи информации необходимо учитывать высоту зданий городских территорий. Определение высоты предмета необходимо и в лесной промышленности, где по высоте деревьев и диаметру их стволов находят массу растущей древесины на участке.

Цель работы:

определить высоту архитектурного сооружения, памятника Петру I.

Для достижения цели были поставлены следующие задачи:

1. Систематизировать знания по темам «Подобные треугольники» и

«Соотношения между сторонами и углами треугольника»;

1. Изучить различные способы определения высоты предмета;

2. Найти высоту памятника Петру I;

3. Составить классификацию погрешностей, влияющих на результат

измерений;

1. Выявить простой и более точный способ определения высоты предмета.

Для решения поставленных задач мы использовали следующие методы:

• изучение,

• эксперимент,

• анализ.

Новизна исследования заключается в самостоятельном нахождении исходных данных для решения поставленной задачи (определить высоту памятника), а также выявлении причин погрешностей, возникающих при различных измерениях, что отсутствует в изученных нами литературных источниках.

Глава I. Историческая справка.

Практическая часть работы посвящена измерению высоты памятника Петру I.

Петр I родился 30 мая (9 июня) 1672 года и умер 28 января (8 февраля) 1725 года. Царь Московский и первый император всероссийский считался одним из наиболее выдающихся государственных деятелей, определивший направление развития России в XVIII веке. Петр был провозглашен царем в 1682 году в 10-летнем возрасте, стал править самостоятельно с 1689 года.

Впервые Петр I прибыл в Архангельск 30 июля 1693 года. Свыше двух месяцев царь провел в Архангельске, где познакомился с корабельным делом и коммерческими операциями торговых людей. 18 сентября того же года Петр I на острове Соломбала собственноручно заложил торговый морской корабль «Святой Павел», положив тем самым начало государственному судостроению в России. Вторично Петр I прибыл в Архангельск 18 мая 1694 года. В этот приезд он совершил путешествие в Соловецкий монастырь и плавание по Белому морю. А 30 мая 1702 года Петр I в третий раз приехал в Архангельск, взяв с собой сына Алексея, большую свиту и пять батальонов гвардии.

18 декабря 1708 года по указу Петра I в числе восьми губерний России была образована Архангельская губерния, и Архангельск стал губернским городом.

По инициативе архангельского губернатора Ивана Васильевича Сосновского был сооружен памятник Петру I и официально открыт в 1914 году в Петровском парке.

Скульптура отлита по модели М.М. Антокольского племянником покойного скульптора в Париже в 1909 году. Является уменьшенной копией установленного в 1903 году памятника Петру I в городе Таганроге. Постамент из серого гранита (архитектор С.А. Пец) изготовили монахи Соловецкого монастыря в каменоломнях Кондострова в Онежской губе Белого моря.

В 1920 году статуя была сброшена с постамента, а на ее месте был сооружен обелиск жертвам интервенции. До 1933 года статуя лежала на берегу, после чего была перемещена в фонд краеведческого музея. В 1948 году памятник воссоздан на нынешнем месте – набережной Северной Двины – историческом месте основания Архангельска.

Царь - реформатор изображен во весь рост в мундире офицера Преображенского полка. Бронзовая скульптура воспринимается как достоверный портретный образ и олицетворение могущества Русского государства.

На гранях пятиметрового постамента из серого гранита архитектор С.А. Пец выбил четыре даты – 1693, 1694, 1702 и 1911. Три первые означают годы посещения Петром I Архангельска, последняя – год создания памятника.

Глава II. Теоретический материал

2.1 Определение.

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

2.2. Признаки подобия треугольников:

1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

3. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

2.3. Свойства подобных треугольников:

• У подобных треугольников периметры относятся как соответствующие стороны.

• У подобных треугольников отношение площадей равно квадрату коэффициента подобия.

• Для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.

2.4. Для произвольного треугольника, стороны которого соответственно равны 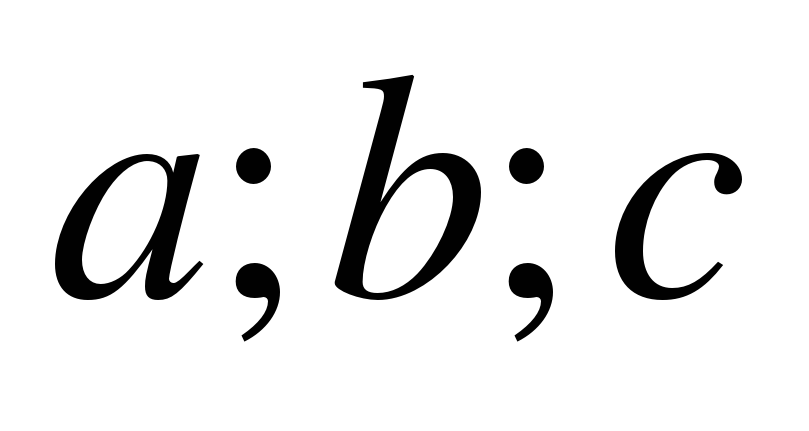, а противолежащие им углы – 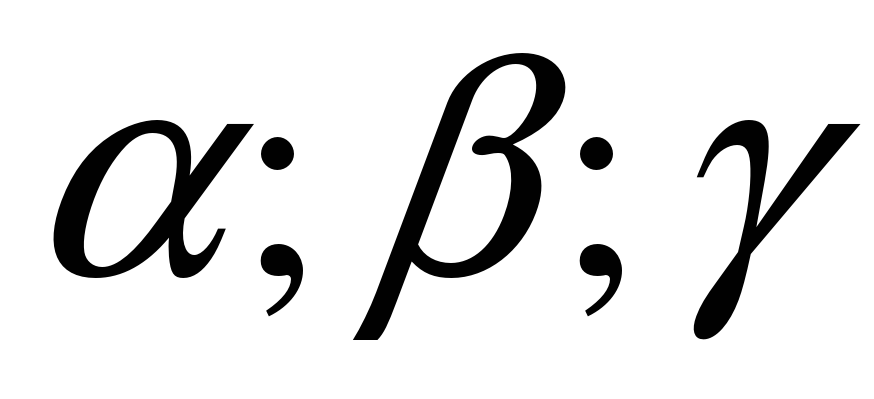справедливы следующие теоремы, устанавливающие соотношения между сторонами и углами треугольника:

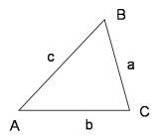
Теорема синусов:

Стороны треугольника пропорциональны синусам противолежащих углов



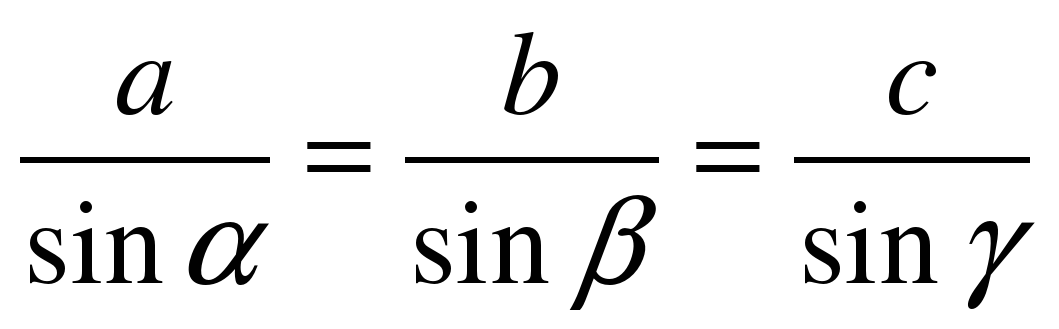
2.5 Теорема косинусов:

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними

Глава Ш. Способы определения высоты предмета

Существует множество различных способов производить определение высоты предмета при помощи весьма незамысловатых приборов и даже без всяких приспособлений.

Для своей работы мы отобрали только те, которые просты в применении.

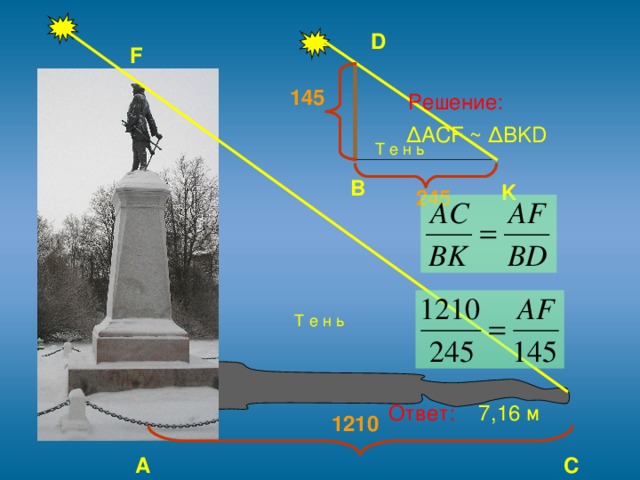
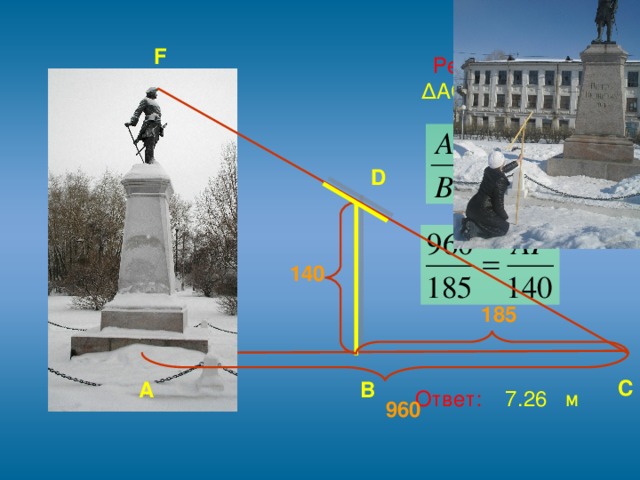
3.1. Самый легкий и самый древний способ – это тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Фалес,- говорит предание,- избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени.

Этим способом очень удобно пользоваться в ясный солнечный день для измерения одиноко стоящих объектов, тень которых не сливается с тенью соседних. Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент. Солнце у нас низко стоит над горизонтом, и тени бывают, равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев, поэтому способ Фалеса в указанном виде применим не всегда.

Но можно изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Для этого надо измерить свою тень (или тень шеста) и вычислить искомую высоту из пропорции,  т.е. высота объекта во столько же раз больше вашей собственной высоты (или высоты шеста), во сколько раз тень объекта длиннее вашей тени (или тени шеста). Это вытекает из первого признака подобия треугольников  (по двум углам).

Итак, мы находимся у памятника Петру I. После измерения длины шеста, длины тени памятника, и тени шеста получаются следующие вычисления:

Решение:

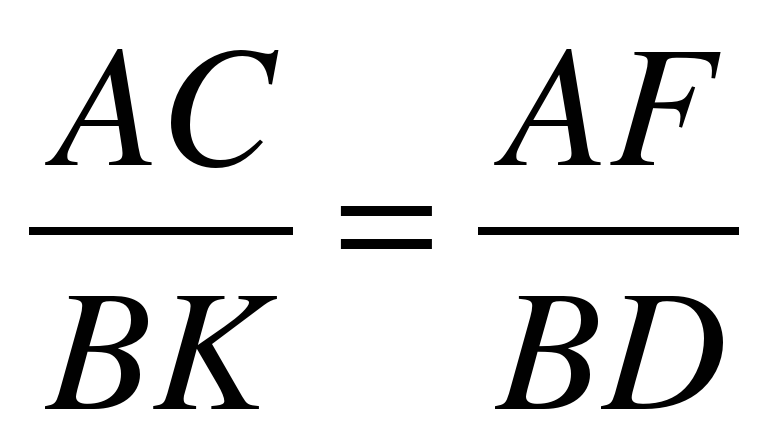
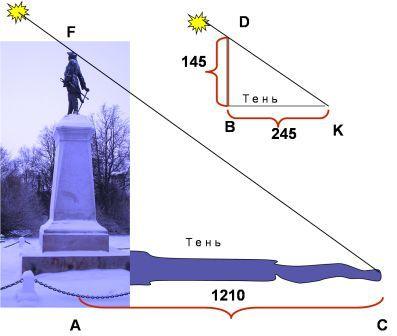∆ACF ~ ∆BKD

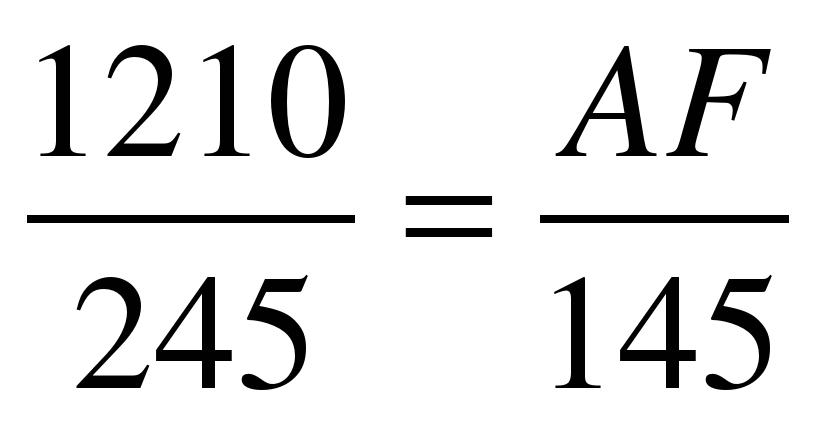
Ответ: 7,16 м

Вывод: После многократных измерений и анализа, допущенных нами ошибок мы получили примерно искомую цифру. Погрешность измерений получалась по следующим причинам:

• поверхность земли не является ровной (памятник находится на холмистой поверхности, зимой вокруг него много сугробов);

• Тень памятника не имеет резких очертаний т.к. солнце не является точечным источником;

• На севере зимой солнце стоит низко над горизонтом. Значит, тень достигает больших размеров и при отсутствии свободного пространства ,она падает на близ лежащие деревья, ограду, дома;

• Затруднительно выполнить измерения от центра подножия памятника;

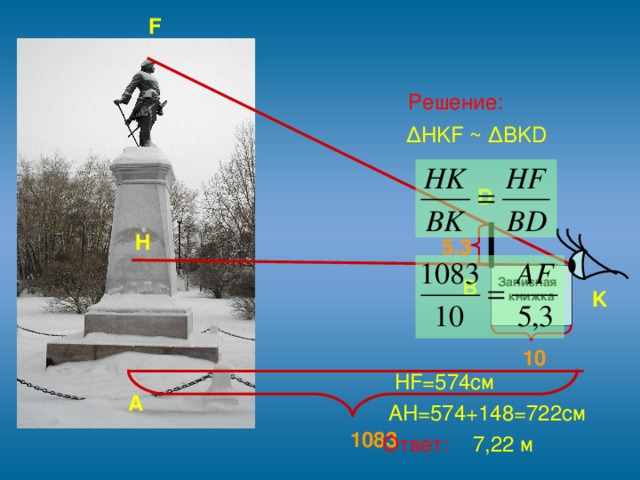
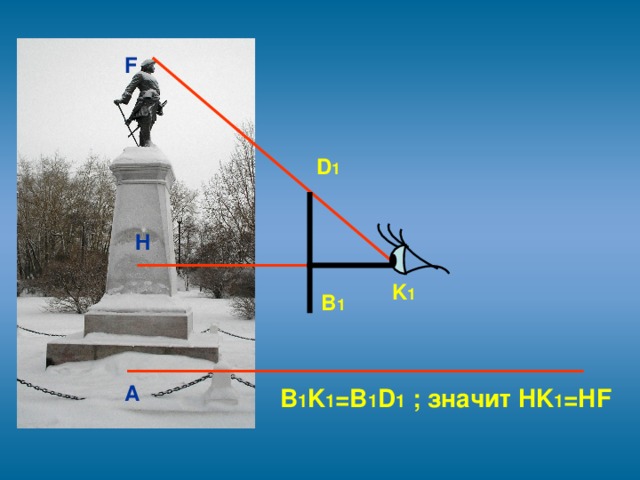
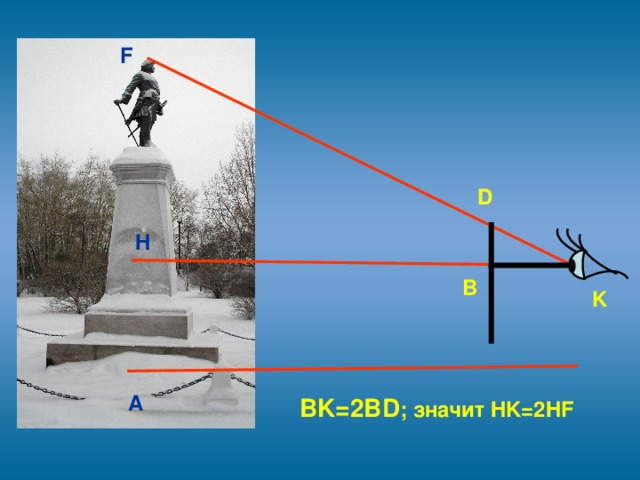
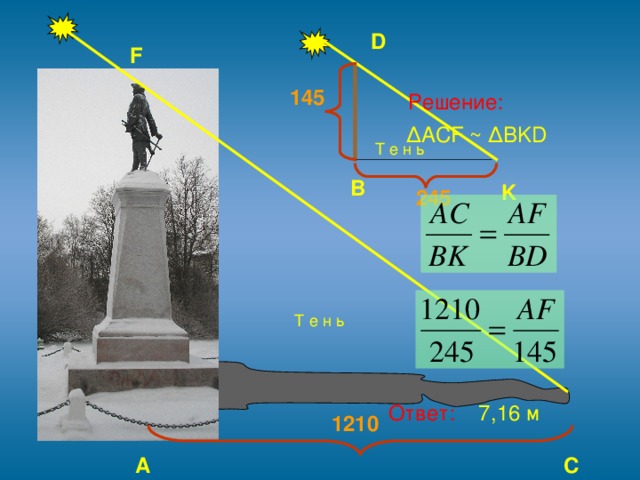
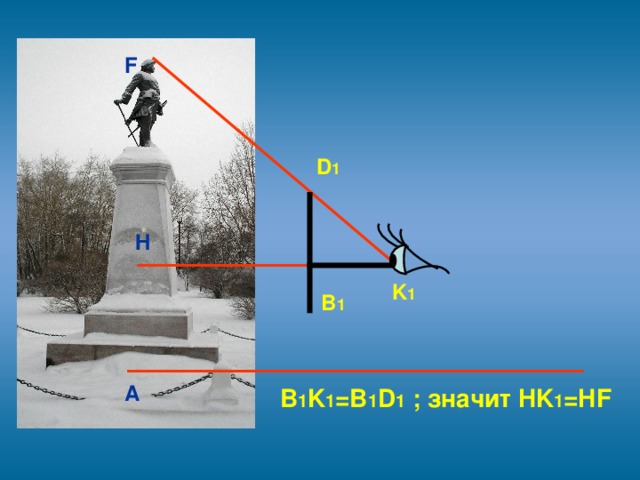
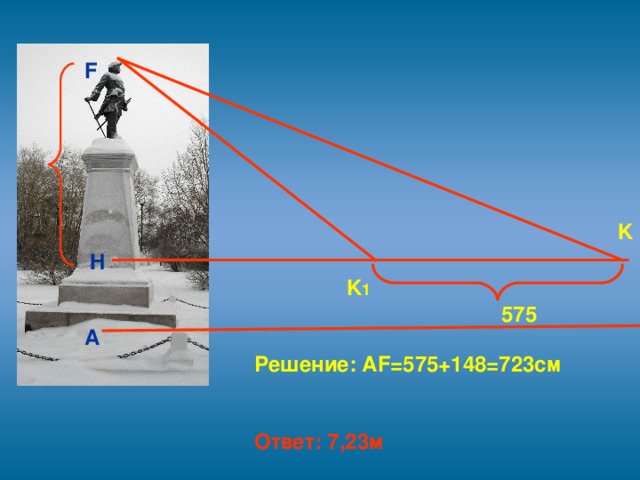
3.2. В качестве прибора для приблизительной оценки недоступной высоты можно воспользоваться и своей карманной записной книжкой, которая снабжена карандашом, всунутым в петельку при книжке. Книжку надо держать возле глаза. Она должна находиться в отвесной плоскости, а карандаш выдвигается над верхним обрезом книжки настолько, чтобы глядя из точки К, видеть вершину F объекта покрытой кончиком D карандаша. Тогда из подобия треугольников  ∆HKF~∆BKD, вычислим длину HF

К найденной величине необходимо прибавить высоту положения глаза над землей.

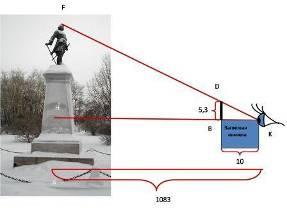Решение:

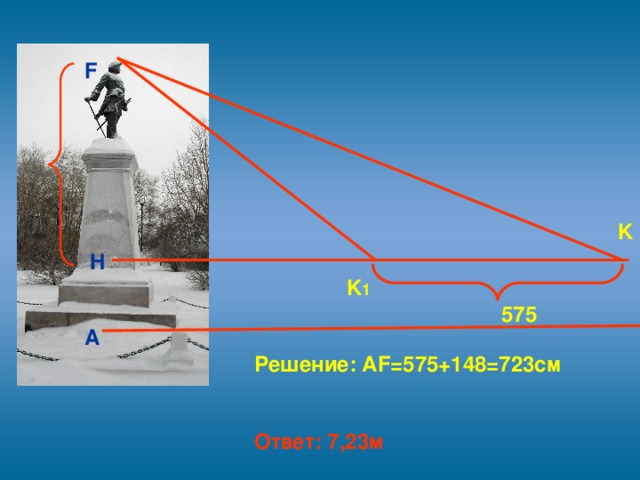
∆HKF~∆BKD,

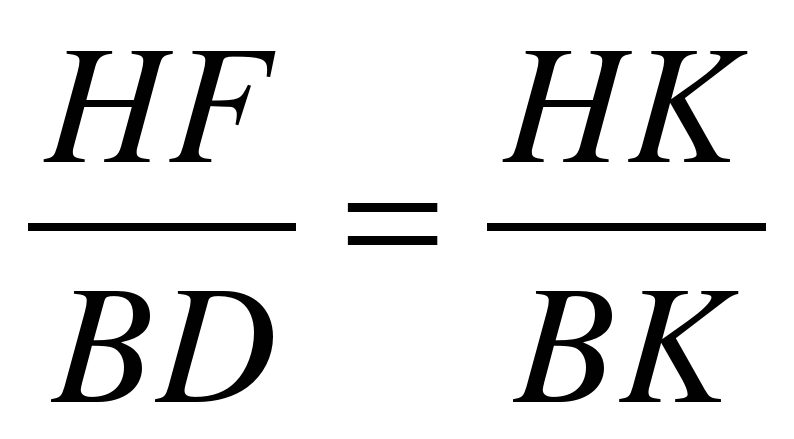
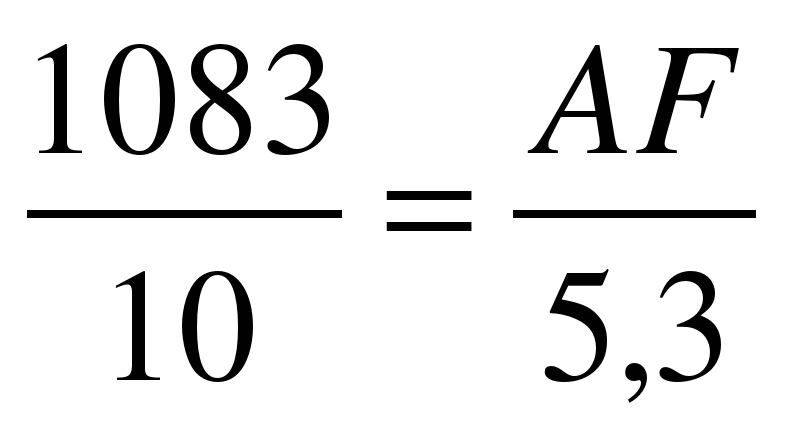
HF=574см;

AH=574+148=722см

Ответ: 7,22 м

Вывод: погрешность измерений получалась по следующим причинам:

• поверхность земли не является ровной (памятник находится на холмистой поверхности, зимой вокруг него много сугробов);

• Затруднительно выполнить измерения от центра подножия памятника;

Сложно держать книжку у глаза горизонтально поверхности земли, обязательно необходим вертикальный отвес.

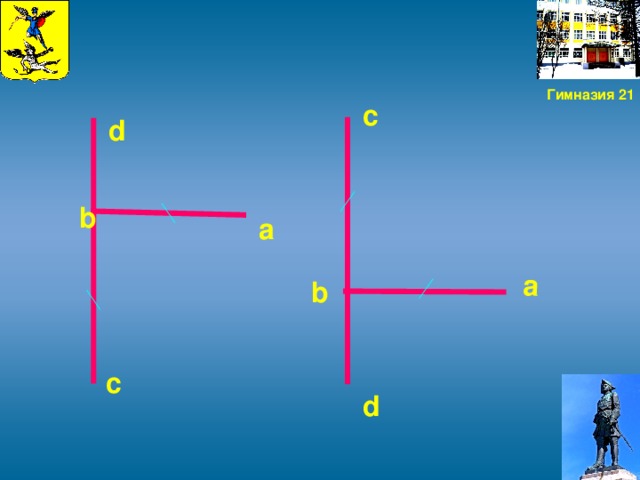
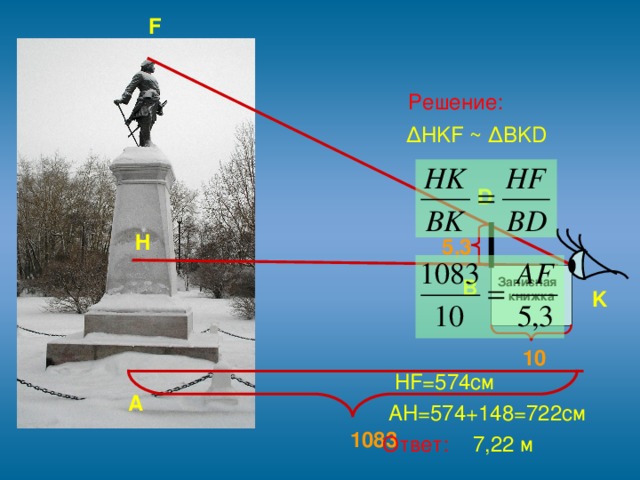
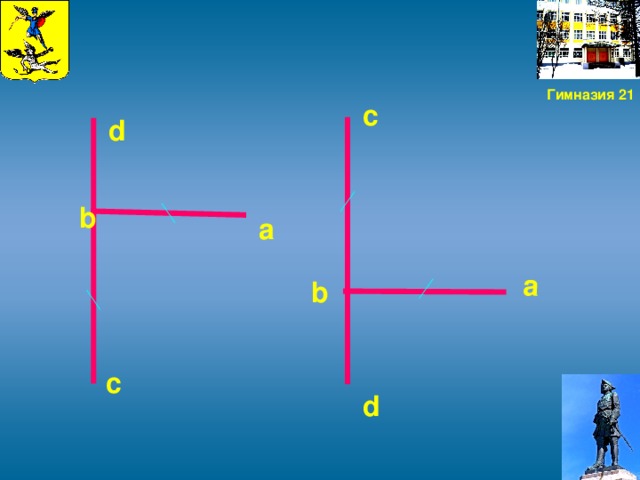
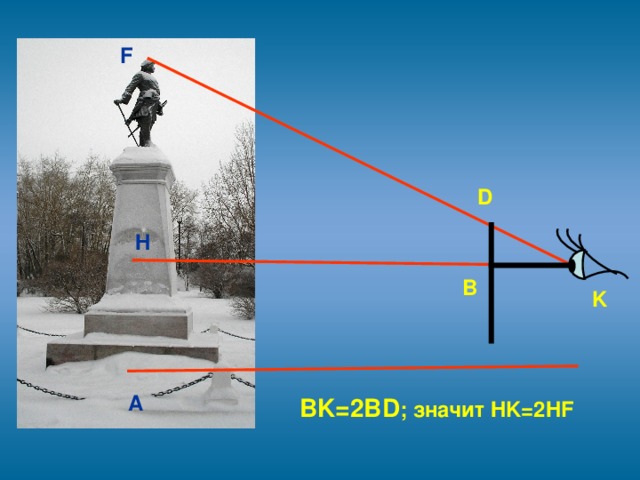
3.3. Иногда случается, что неудобно подойти вплотную к основанию измеряемого объекта. И чтобы измерить его высоту, был придуман остроумный прибор, который можно изготовить самому. Две планки ab и cd скрепляются под прямым углом так, чтобы ab=bc, а bd =1/2 ab.

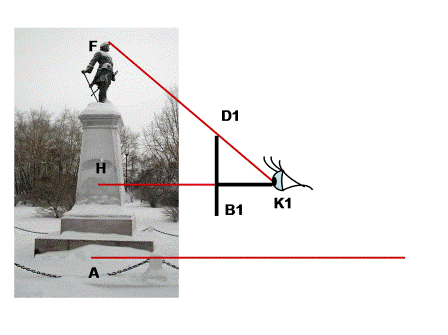
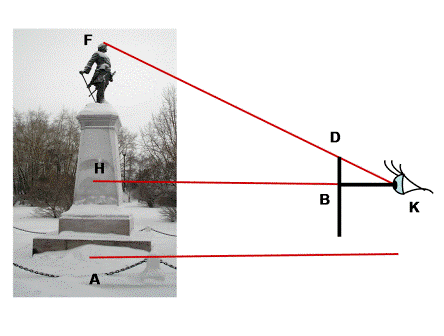
Чтобы измерить им высоту, держат его в руках, направив планку cd вертикально, и становятся последовательно в двух местах: сначала в точке К₁, где располагают прибор концом с вверх, а затем в точке К, подальше, где прибор держат вверх концом d. Точка К₁ избирается так, чтобы, глядя из a на конец c, видеть его на одной прямой с верхушкой

объекта. Точку же К_ отыскивают так, чтобы, глядя из а на d, видеть ее на одной прямой с верхушкой объекта. В отыскании этих двух точек К и К₁ заключается всё измерение, потому что искомая часть высоты объекта HF=KK₁= HK- HK₁. Затем останется прибавить высоту человека до глаз.

Вывод: погрешность измерений получалась по следующим причинам:

• поверхность земли не является ровной (памятник находится на холмистой поверхности, зимой вокруг него много сугробов);

• Сложно держать прибор у глаза горизонтально поверхности земли, обязательно необходим вертикальный отвес.

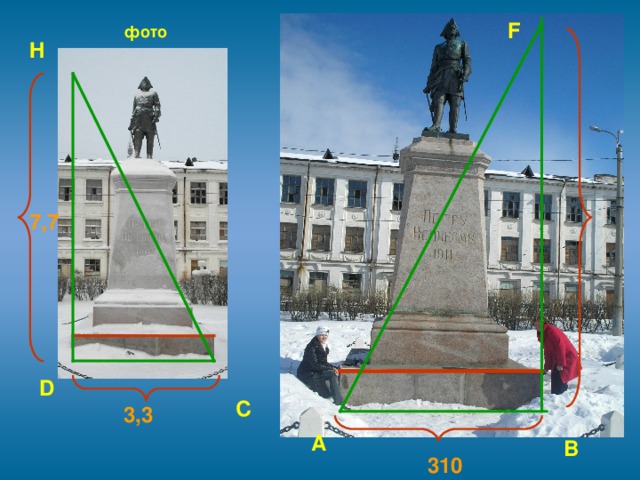
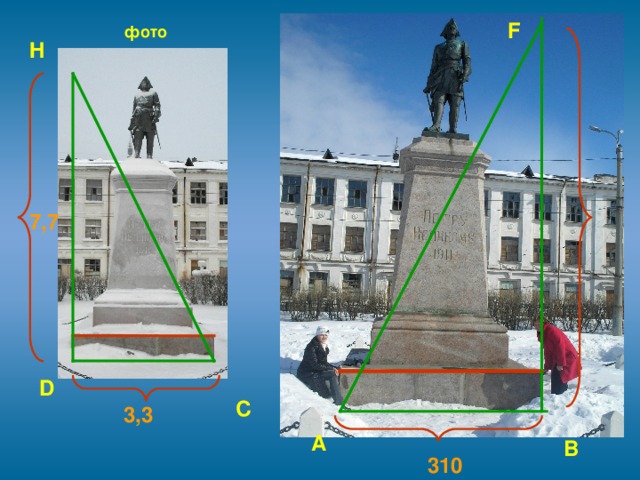
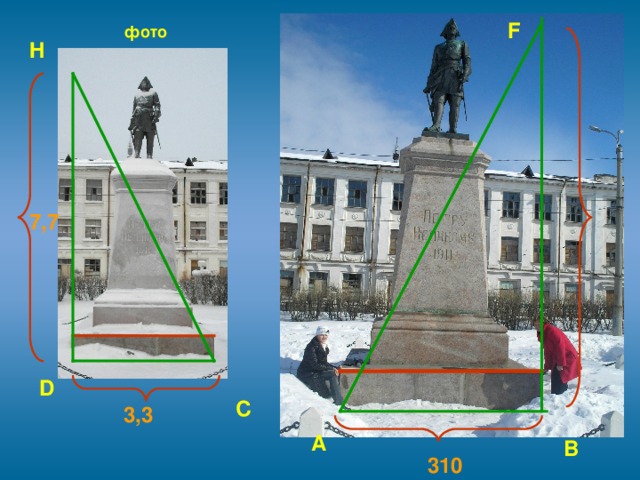
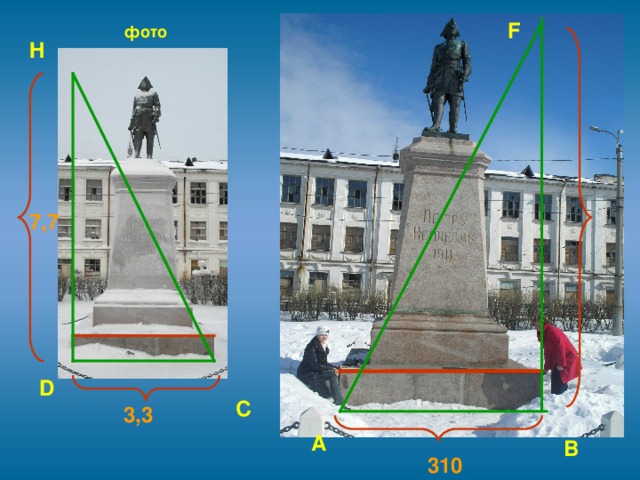
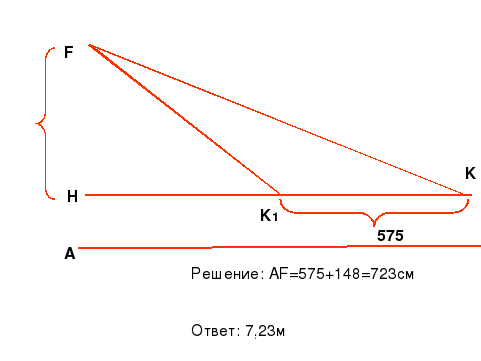
3.4. Современным и простым является способ определения высоты при помощи фотографии. Для этого необходимо сфотографировать объект исследования и измерить длину одного из предметов, который попадает на эту фотографию (или часть объекта).

А ещё проще около объекта положить метровую палку, затем сделать фотоснимок. Далее из отношения длин на фотографии можно найти истинный размер предмета.

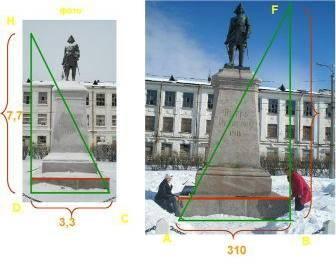
Решение:

∆ABF ~ ∆CDH

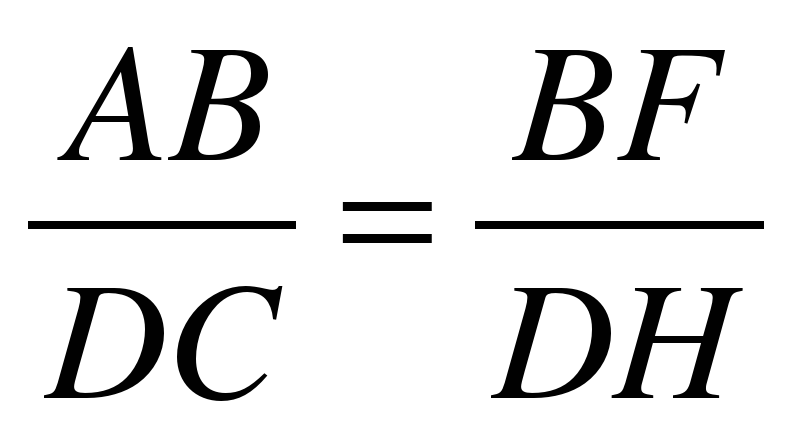
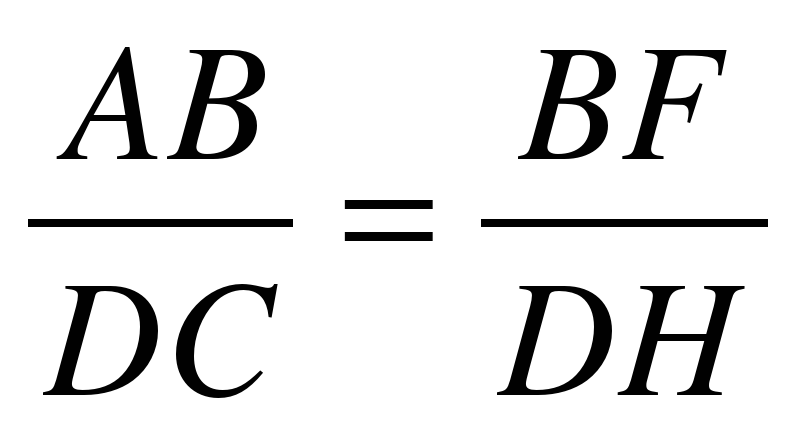
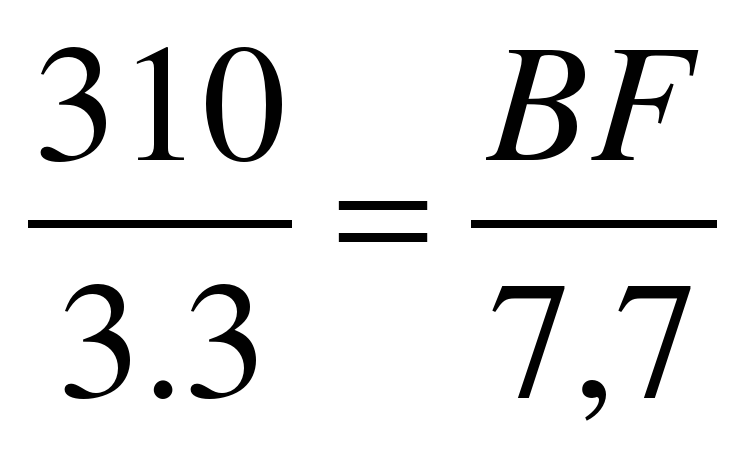
Ответ: BF=7,23м

Вывод: на первый взгляд метод не имеет недостатков, причем, чем крупнее фотография, тем точнее результат измерения. Однако, мы обнаружили, что современная техника (которая была в нашем распоряжении) цифровой фотоаппарат, компьютер, принтер дают искажение реального объекта. Причем, чем крупнее фотография, тем больше погрешность. Но, мы получили искомый результат с помощью фотоснимка, сделанного на плёночном фотоаппарате.

3.5. Вот еще своеобразный способ определения высоты объекта при помощи зеркала. На некотором расстоянии от измеряемого объекта, на ровной земле в точке В кладут горизонтально зеркальце и отходят от него назад в такую точку С, стоя в которой мы видим в зеркальце верхушку F объекта. Тогда объект (AF) во столько раз выше роста наблюдателя (CD), во сколько раз расстояние BA от зеркала до объекта больше расстояния CB от зеркала до наблюдателя. Данный способ основан на законе отражения света.

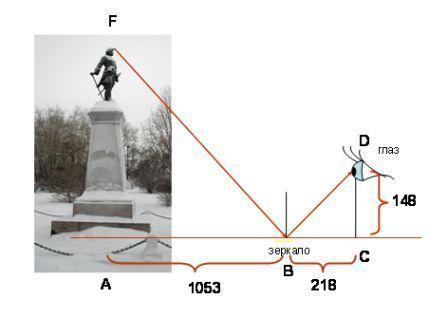Решение:

∆AFB~∆CDB

;

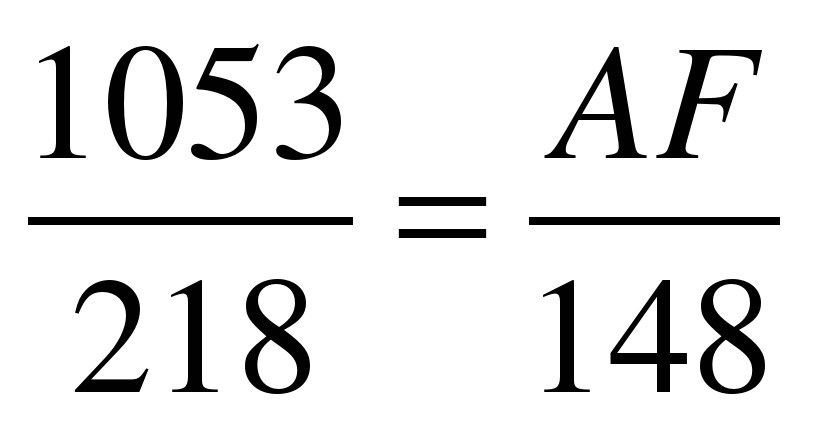
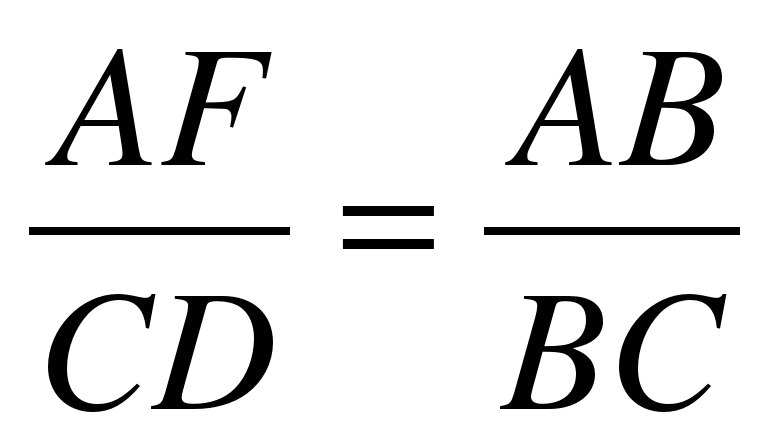AF= 7,14м; Ответ: 7,14м

Вывод:

• поверхность земли не является ровной (памятник находится на холмистой поверхности, зимой вокруг него много сугробов);

• Затруднительно выполнить измерения от центра подножия памятника;

• Зеркало должно лежать горизонтально и в одной плоскости с основанием памятника .

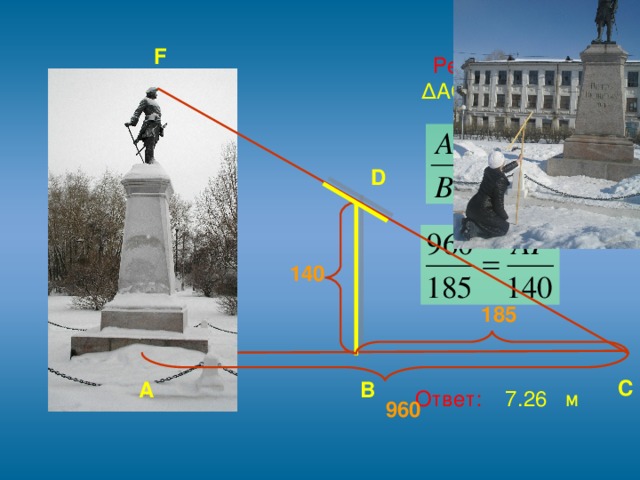
3.6. Высоту предмета можно определить при помощи шеста с наклонной планкой. Для этого устанавливаем шест на некотором расстоянии от объекта. Направляем планку на вершину измеряемого предмета. Находим точку С на земле, где будет пересекаться линия планки с поверхностью земли. Далее выполняем измерения от объекта до точки С, от шеста до точки С, и длину шеста.

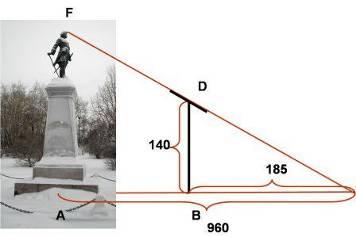
Решение:

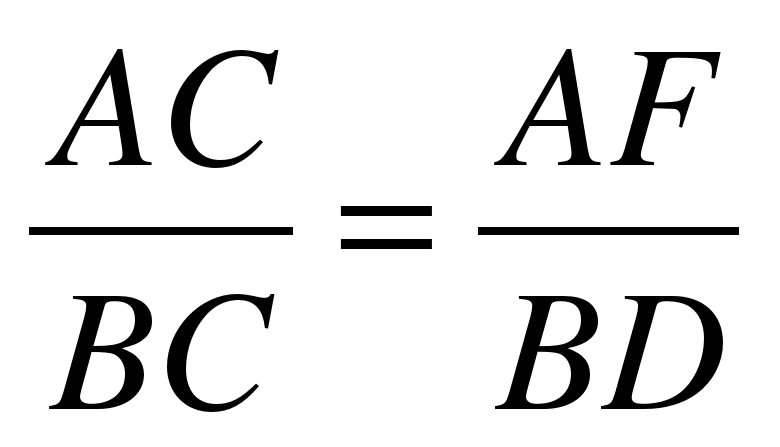∆ACF ~ ∆BCD

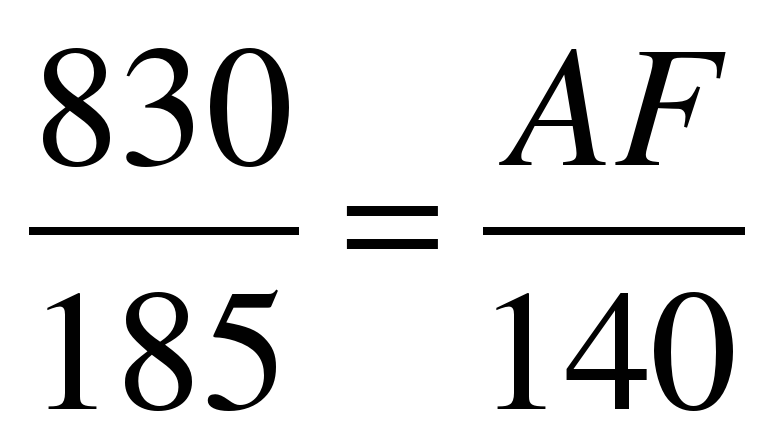
AF=7,26м

Ответ: 7,26м

Вывод: погрешность измерений получалась по следующим причинам:

• поверхность земли не является ровной, (памятник находится на холмистой местности, зимой вокруг него много сугробов);

• Затруднительно выполнить измерения от центра подножия памятника;

• Сложно найти местоположение точки С (мы воспользовались дополнительной рейкой).

Заключение

Итак, благодаря знаниям, полученным на уроках геометрии по темам «Подобные треугольники» и «Соотношения между сторонами и углами треугольника», мы получили примерную цифру известной величины-7,2 м.

Используя различные способы определения высоты предмета, мы выделили наиболее доступные с практической точки зрения:

• При помощи тени;

• При помощи записной книжки;

• При помощи прибора из двух планок;

• При помощи фотографии;

• При помощи зеркала.

Мы составили классификацию погрешностей при измерениях, влияющих на результат.

Трудно сказать, каким способом лучше пользоваться для определения высоты объекта. Все зависит от имеющихся подручных средств, от места положения объекта, от точности, которая необходима.

Практическая значимость:

Интересен факт: из беседы с лесниками, работающими в Архангельской области, мы выяснили, что при наличии у них профессиональных приборов для измерения высоты дерева (мерная вилка, высотомер), они часто используют метод записной книжки, в которую и записывают свои результаты.

Некоторые из рассмотренных нами методов используются компаниями сотовой связи. Так, например, при помощи спутников делают фотоснимки городских территорий. На снимках фиксируются тени зданий, благодаря которым и определяют высоту сооружений.

Перспектива:

На уроках геометрии рассматривается задача по определению расстояния до недоступной точки. В следующей работе нам хотелось бы рассмотреть и эту задачу.

Применение:

Наше исследование можно использовать при проведении практических работ на уроках геометрии, а также во внеклассных мероприятиях, например, туристических слетах.

Библиография:

1. Атанасян Л.С. и др. Геометрия для 7-9 классов общеобразовательных учреждений – М.:Просвещение, 2009

2. Атрохин В.Г. Основы лесоводства и лесной таксации. М.: Лесная промышленность, 1971

3. Глейзер Г.И. История математики в школе. М.:Просвещение, 1964

4. Крамор В.С. Повторяем и систематизируем школьный курс геометрии. М.: Просвещение, 1992

5. Перельман Я.И. Занимательная геометрия. М.: ВАП, 1994

6. Погорелов В.В., Шавук В.С. Теоретическое обоснование способа измерения высот зданий по одиночному спутниковому изображению. М.: Геодезия и картография, №4, 2008

7. Прасолов В.В. Задачи по планиметрии. Часть 2. М.: Наука, 1991

8. Селезнев А.Г. Архангельск и его окрестности. А.: Северо-западное книжное издательство, 1967

9. Фруменков Г.Г. и другие. Летопись города Архангельска. А.: Северо.-Западное книжное издательство, 1990.

Приложение 1

Классификация погрешностей измерений

Приложение 2

Фотоотчёт.

Метод записной книжки. С помощью прибора из двух планок.

Метод фотографии. Измеряем высоту до уровня глаз

15

Определение высоты предмета

на примере

памятника Петру I

Цель:

гимназия 21

Определение высоты памятника Петру I

с применением различных способов измерений

Задачи

• Систематизировать знания по темам «Подобные треугольники», «Соотношения между сторонами и углами треугольника»

• Изучить различные способы определения высоты предмета

• Найти высоту памятника Петру I

• Составить классификацию погрешностей, влияющих на результат измерений

• Выявить простой и наиболее точный способ нахождения высоты предмета

• 1693г - знакомство с корабельным делом, собственноручно заложил корабль

«Св. Павел»

• 1694г - посещение Соловецкого монастыря

• 1702г - лично руководил строительством крепостных сооружений

Петр I ( 1672г-1725г)

1920г

1914г

1948г

Способы

нахождения высоты предмета

• При помощи тени
• При помощи записной книжки
• При помощи самодельного прибора
• При помощи фотографии
• При помощи зеркала
• При помощи шеста с планкой

21 гимназия

гимназия 21

Определение высоты при помощи тени

Полуденное зимнее

солнце в Архангельске

D

F

Решение:

∆ ACF ~ ∆BKD

Ответ: 7,16 м

145

Т е н ь

B

K

245

Т е н ь

1210

C

A

гимназия 21

Определение высоты при помощи записной книжки

Записная

книжка

F

Решение:

∆ HKF ~ ∆BKD

HF= 574см

AH=574+148=722 см

Ответ: 7, 22 м

D

H

5,3

B

Записная

книжка

K

10

A

1083

Гимназия 21

Определение высоты

при помощи

самодельного прибора

d

c

a

b

Гимназия 21

d

b

a

c

F

D 1

H

K 1

B 1

A

B 1 K 1 =B 1 D 1 ; значит HK 1 =HF

F

D

H

B

K

A

BK=2BD ; значит HK=2HF

F

K

H

K 1

575

A

Решение: А F =575+148=723см

Ответ: 7,23м

гимназия 21

Определение высоты при помощи фотографии

C

F

фото

H

7,7

D

3,3

А

В

310

C

F

фото

H

Решение:

∆ ABF ~ ∆CDH

Ответ: 7,23 м

7,7

D

3,3

А

В

310

гимназия 21

Определение высоты при помощи зеркала

F

Решение:

∆ ABF ~ ∆CBD

Ответ: 7,14 м

D

глаз

148

зеркало

C

B

А

218

1053

зеркало

гимназия 21

Определение высоты при помощи шеста с вращающейся планкой

F

Решение:

∆ ACF ~ ∆BCD

Ответ: 7.26 м

D

140

185

С

В

А

960

Заключение

• Изучили различные методы определения высоты предмета
• Получили высоту приближенно равную истинному размеру памятника (7,2 м)
• Выявили погрешности измерений
• Пришли к выводу, что выбор способа определения высоты зависит от подручных средств, места положения объекта и точности, которая необходима.

гимназия 21

Спасибо

за

внимание!

Определение высоты предмета

на примере

памятника Петру I

Цель:

гимназия 21

Определение высоты памятника Петру I

с применением различных способов измерений

Задачи

• Систематизировать знания по темам «Подобные треугольники», «Соотношения между сторонами и углами треугольника»

• Изучить различные способы определения высоты предмета

• Найти высоту памятника Петру I

• Составить классификацию погрешностей, влияющих на результат измерений

• Выявить простой и наиболее точный способ нахождения высоты предмета

• 1693г - знакомство с корабельным делом, собственноручно заложил корабль

«Св. Павел»

• 1694г - посещение Соловецкого монастыря

• 1702г - лично руководил строительством крепостных сооружений

Петр I ( 1672г-1725г)

1920г

1914г

1948г

Способы

нахождения высоты предмета

• При помощи тени
• При помощи записной книжки
• При помощи самодельного прибора
• При помощи фотографии
• При помощи зеркала
• При помощи шеста с планкой

21 гимназия

гимназия 21

Определение высоты при помощи тени

Полуденное зимнее

солнце в Архангельске

D

F

Решение:

∆ ACF ~ ∆BKD

Ответ: 7,16 м

145

Т е н ь

B

K

245

Т е н ь

1210

C

A

гимназия 21

Определение высоты при помощи записной книжки

Записная

книжка

F

Решение:

∆ HKF ~ ∆BKD

HF= 574см

AH=574+148=722 см

Ответ: 7, 22 м

D

H

5,3

B

Записная

книжка

K

10

A

1083

Гимназия 21

Определение высоты

при помощи

самодельного прибора

d

c

a

b

Гимназия 21

d

b

a

c

F

D 1

H

K 1

B 1

A

B 1 K 1 =B 1 D 1 ; значит HK 1 =HF

F

D

H

B

K

A

BK=2BD ; значит HK=2HF

F

K

H

K 1

575

A

Решение: А F =575+148=723см

Ответ: 7,23м

гимназия 21

Определение высоты при помощи фотографии

C

F

фото

H

7,7

D

3,3

А

В

310

C

F

фото

H

Решение:

∆ ABF ~ ∆CDH

Ответ: 7,23 м

7,7

D

3,3

А

В

310

гимназия 21

Определение высоты при помощи зеркала

F

Решение:

∆ ABF ~ ∆CBD

Ответ: 7,14 м

D

глаз

148

зеркало

C

B

А

218

1053

зеркало

гимназия 21

Определение высоты при помощи шеста с вращающейся планкой

F

Решение:

∆ ACF ~ ∆BCD

Ответ: 7.26 м

D

140

185

С

В

А

960

Заключение

• Изучили различные методы определения высоты предмета
• Получили высоту приближенно равную истинному размеру памятника (7,2 м)
• Выявили погрешности измерений
• Пришли к выводу, что выбор способа определения высоты зависит от подручных средств, места положения объекта и точности, которая необходима.

гимназия 21

Спасибо

за

внимание!