
«Учебно-методическая разработка: Логические задачи»
Выполнила: студентка группы НК-21
Точилкина Екатерина
Преподаватель:
Лихачева Екатерина Сергеевна
г.о.Тольятти
Содержание
Введение
Задачи на переливание
Задачи на взвешивание
Задачи типа «Кто есть кто?»
Задачи со спичками
Задачи на логику и рассуждение
Истинноностные задачи
Цель:
Познакомиться понятиями логика и логические задачи;
Научиться решать логические задачи;
Способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное;
Развивать осознанную математическую речь;
Задачи:
Формирование логического, абстрактного, эвристического, системного мышления.
Развитие познавательной активности;
Развитие памяти и внимания;
Введение
Что такое логика и логические задачи?
Логика – наука о верном, правильном мышлении. Человек, мыслящий логически, способен к последовательному и связному мышлению с использованием доказательств и выявлением закономерностей.
Говоря о логических задачах, стоит оговориться: задач, незадействующих при решении логику, не существует в принципе. Для решения любой задачи характерны последовательность в решении, учет всех взаимосвязей фактов, наличие аргументов.
Задачи на логику – это такие задачи, при решении которых определяющим фактором является обнаружение связей между данными задачи и их анализ, при чем, результатом является составление последовательных суждений, а любые вычисления и построения играют вспомогательную роль или отсутствуют.
Зачем нужны в школьной программе по математике задачи на развитие логики?
Логические задачи, как понятно из названия, развивают логику, но почему эти задачи должны решаться на уроках математики? По многим причинам. Во-первых, немалая доля всей информации, которую дают учебники по математике, связана исключительно с логикой (доказательства большинства теорем по геометрии и некоторых по алгебре). Во-вторых, многие задачи по математике подразумевают использование навыков логического мышления (модуль «Реальная математика» в тестах). В-третьих, говоря о решении любой задачи, нельзя не упомянуть о логике. Но в любом школьном курсе математики очень мало логических задач, и это значит, что изучению такой важной науки, Логики, уделяется очень мало внимания.
Как следует преподносить логические задания?
Для начала, выдав задание, не стоит указывать на особенность его решения. Узнав ход мыслей обучающихся в этот момент, можно понять, насколько развита у них смекалка. Если они решили задачу, стоит попросить объяснить решение, аргументировать свой ответ. На этом этапе при возникновении трудностей с аргументацией важно активно помогать обучающимся. Если решение вызвало затруднение, нужно направить мысли в нужном направлении, подсказав один-два суждения из цепочки рассуждений. Если задача не дается обучающемуся, необходимо объяснить каждое суждение. Целью подобных заданий является увлечение ребенка изучаемым предметом, процессом осмысления информации и развитие логики. Успехи в решении логических задач стоит поощрять похвалой.
1.Задачи на переливание
1. Как, имея пятилитровое ведро и девятилитровую банку, набрать из реки ровно три литра воды
Ответ:
Заполняем 9-литровую банку и заливаем из нее в 5-литровое ведро. (Далее 5-литровка и 9-литровка). В 9 - литровке 4 литра. выливаем воду из 5-литровки и заливаем туда 4 литра из 9-литровки. Заполняем 9-литровку и выливаем оттуда 1 литр в пятилитровую. Выливаем воду из 5-литровки, и заполняем 5-литровку из 9-литровки. Всё! В 9-литровке теперь 3 литра. Если 5 литров в ведре не нужно, их можно вылить.
2. Двое должны разделить поровну 8 вёдер кваса, находящегося в большом бочонке. Но у них есть ещё только два пустых бочонка, в один из которых входит 5 вёдер, а в другой - 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками? Решите задачу двумя способами
Ответ:
решение 1
Большой 5-ведёрн. 3-ведёрн
До переливания 8 0 0
После 1-го переливания 3 5 0
После 2-го переливания 3 2 3
После 3-го переливания 6 2 0
После 4-го переливания 6 0 2
После 5-го переливания 1 5 2
После 6-го переливания 1 4 3
После 7-го переливания 4 4 0
решение
Большой 5-ведёрн. 3-ведёрн.
До переливания 8 0 0
После 1-го переливания 5 0 3
После 2-го переливания 5 3 0
После 3-го переливания 2 3
После 4-го переливания 2 5 1
После 5-го переливания 7 0 1
После 6-го переливания 7 1 0
После 7-го переливания 4 1
После 8-го переливания 4 4 0
3. Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л.
Ответ:
Сначала наливаете 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л.-4 литра, в 8л-3литра, а в 5л.-5 литров.
Переливаете из 5л. в 12л. всю воду (или что там за жидкость), а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л.
Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр.
Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л.
4. Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Ответ:
Наливаем кастрюлю.
Переливаем воду из кастрюли в банку.
Наливаем кастрюлю.
Доливаем полную банку, и в кастрюле остается 3 литра.
5. Два сосуда и кран с водой.
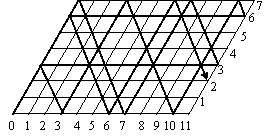
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?
Ответ:
Если сначала наполнить 11-литровый сосуд, то потребуется 18 переливаний, а если 7-литровый, то, как следует из рисунка, – всего 14.
2.Задачи на взвешивание
1. Мешки с золотом
Есть 10 мешков с золотом. В каждом по 10 монет. В девяти мешках монеты настоящие, а в одном - все фальшивые. Одна настоящая монета весит 5 грамм, а фальшивая - 4 грамма. Есть весы, показывающие вес в граммах.
Необходимо за одно взвешивание точно определить, в каком мешке фальшивые монеты
Ответ:
Пронумеруем мешки от 1 до 10. Вытащим из первого 1 монету, из второго 2, из третьего 3 и так далее. Затем возьмем всю эту кучу монет и положим на весы. Если бы они все были настоящие, то общий вес составил бы 275 грамм (т. к. мы вытащили в общей сложности 55 монет). Но в одном из мешков были фальшивые. Если это был первый мешок, то вес будет на 1 грамм меньше (т. к. мы взяли оттуда 1 монету). Если фальшивые были во втором, то на 2 грамма меньше. И так далее.
2. Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.
Ответ
Взвешиваешь 50 и 50 монет:
1) Равенство:
Беpем оставшуюся монету и ставим ее в левую кучку вместо одной из имеющихся там
1.1 Левая кучка тяжелее => фальшивая монета тяжелее
1.2 Левая кучка легче => фальшивая монета легче
2) Hеpавенство
Беpем более тяжелую кучку и разбиваем ее на две кучки по 25 монет.
2.1 Вес кучек одинаковый => фальшивая монета легче
2.2 Вес кучек неодинаковый => фальшивая монета тяжелее
3. У вас 10 мешков с монетами, по 1000 монет в каждом. В одном из мешков все монеты фальшивые. Настоящая монета весит 1 г., фальшивая – 1,1 г.. Имея точные весы, как определить мешок с фальшивыми монетами с помощью только одного взвешивания?
Что если неизвестно, сколько мешков было с фальшивыми монетами?
Ответ:
Если только один мешок наполнен фальшивыми монетами, тогда возьмите из первого мешка одну монетку, из второго мешка две монетки.... и десять монеток из десятого мешка. Взвесьте собранные монетки. Сравните показание весов с тем, которое было бы в идеале, если бы все монеты были бы настоящими. Полученная разница (число граммов) укажет на номер мешка с фальшивыми монетами.
Если же фальшивые монеты не в одном мешке, а в нескольких, то вариантов решения гораздо больше. Для примера дам такой вариант: 1, 2, 4, 10, 20, 50, 100, 200, 500 и 1000.
4. На рождественской ёлке висят три пары шаров: два белых, два голубых и два красных. Внешне шары одинакового размера. Однако в каждой паре есть один лёгкий и один тяжёлый шар. Все лёгкие шары весят между собой одинаково, и так же все тяжёлые шары. С помощью двух взвешиваний на чашечных весах определите все лёгкие и все тяжёлые шары.
Ответ:
Положите один красный и один белый шар на левую чашу весов, а на правую шачу один синий и второй белый шар. Если достигнуто равновесие, то очевидно, что на каждой чаше есть один тяжёлый и один лёгкий шар. Поэтому достаточно сравнить два белых шара, чтобы узнать ответ на интересующий нас вопрос. Однако если после первого взвешивания равновесие не достигнуто, то на той стороне, что тяжелее, лежит тяжёлый белый шар. Следующим логическим шагом будет сравнение веса уже взвешенного красного шара и еще не взвешенного синего шара.
После этого Вам уж точно должно стать ясно, какие шары лёгкие, а какие тяжёлые.
5. Имеется девять мешков: восемь с песком и один – с золотом. Мешок с золотом только чуть тяжелее. Вам даётся два взвешивания на чашечных весах, чтобы найти мешок с золотом.
Ответ:
Разделите девять мешков на три группы по три мешка каждая. Взвесьте две группы. Таким образом Вы узнаете, в какой из групп мешок с золотом. Теперь выберите 2 мешка из той группы, где точно есть мешок с золотом, и взвесьте их.
3.Задачи типа «Кто есть кто?»
1. Три клоуна Бим, Бам и Бом вышли на арену
в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета
рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными.
Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны?
Ответ:
Рубашка Бама синяя, а Бома — зелёная.
Туфли Бома не могут быть ни красными, ни зелёными (ибо зелёные туфли у Бама).
Поскольку туфли Бама зелёные, то туфли Бома не могут быть ни красными, ни зелёными. Значит, они синие. Биму остаются красные туфли. Поэтому и рубашка у него красная. Тогда рубашка Бама синяя, а Бома — зелёная.
2. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
| Имя | Юра |
|
|
| Профессия |
| врач |
|
| Увлечение |
| туризм |
|
Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра. Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем:
| Имя | Юра | Тимур | Влад |
| Профессия | физик | врач | юрист |
| Увлечение | бег | туризм | регби |
Ответ: Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
3. 5 разных человек в 5 разных домах разного цвета, курят 5 разных марок сигарет, выращивают 5 разных видов животных, пьют 5 разных видов напитков.
Вопрос: Кто выращивает рыбок?
Норвежец живет в первом доме.
Англичанин живет в красном доме.
Зеленый дом находится непосредственно слева от белого.
Датчанин пьет чай.
Тот, кто курит Rothmans, живет рядом с тем, кто выращивает кошек.
Тот, кто живет в желтом доме, курит Dunhill.
Немец курит Marlboro.
Тот, кто живет в центре, пьет молоко.
Сосед того, кто курит Rothmans, пьет воду.
Тот, кто курит Pall Mall, выращивает птиц.
Швед выращивает собак.
Норвежец живет рядом с синим домом.
Тот, кто выращивает лошадей, живет в синем доме.
Тот, кто курит Philip Morris, пьет пиво.
В зеленом доме пьют кофе.
Ответ:
|
| 1 | 2 | 3 | 4 | 5 |
| Цвет дома | желтый | синий | красный | зеленый | белый |
| Напиток | вода | чай | молоко | кофе | пиво |
| Животное | кошки | лошади | птицы | рыбки | собаки |
| Сигареты | Dunhill | Rothmans | Pall Mall | Marlboro | Philip Morris |
| Национальность | норвежец | датчанин | англичанин | немец | швед |
4. Атос, Портос и Арамис в соревновании по фехтованию заняли три первых места. Какое место занял каждый из них, если Портос занял не второе и не третье место, а Арамис – не третье
Решение:
Условия задачи достаточно просты, чтобы воспользоваться методом рассуждений.
Портос занял не не второе и не третье место, значит он – первый. Из оставшихся мест Арамис – не третий, т. е. он второй. Атосу осталось третье место.
Ответ: Портос – первый, Арамис – второй, Атос – третий.
5. В бутылке, стакане, кувшине и банке находятся «Пепси», «Кока-кола», квас и «Спрайт». Известно, что «Спрайт» и «Пепси» не в бутылке, сосуд с «Кока-колой» находится между кувшином и сосудом с квасом, в банке – не «Кока-кола» и не «Спрайт». Стакан находится около банки и сосуда с «Пепси». Как распределены эти жидкости по сосудам?
Решение
Воспользуемся табличным методом.
Из условий задачи получаем таблицу с запретами:
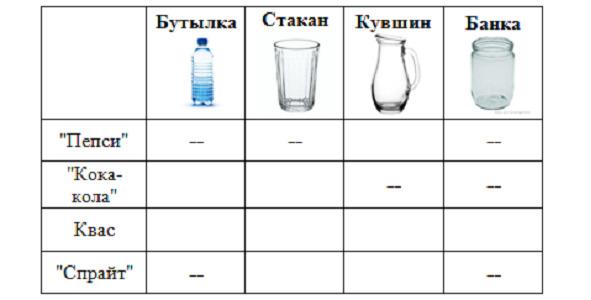
Так как каждая жидкость находится только в одном сосуде, то в в каждой строчке и каждом столбце может стоять только один «+». Взглянув на таблицу, можно сделать вывод, что «Пепси» в кувшине, а квас в банке. Получаем новую таблицу:

Теперь можно сказать, что «Спрайт» – в стакане, а «Кока-кола» в бутылке.
Ответ. Квас в банке; «Пепси» в кувшине; «Кока-кола» в бутылке; «Спрайт» в стакане.
4.Задачи со спичками
Переложите четыре спички из шестнадцати, чтобы получилось три квадрата

Ответ: 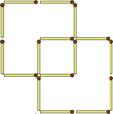

Исправьте равенство так, чтобы оно стало верным, не дотрагиваясь, ни до одной спички (нельзя поджигать, перемещать, передвигать и т. д.).
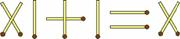
Ответ: 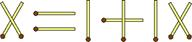
Переложите три спички из двенадцати так, чтобы получилось четыре одинаковых квадрата из трех.
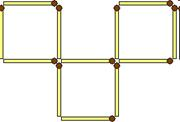 Ответ:
Ответ: 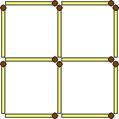
Добавьте нечетное количество спичек, разделив квадрат 4х4 (16 спичек) на четыре области по 4 клетки каждая. Гнуть, ломать и перекрещивать спички нельзя.
 Ответ:
Ответ: 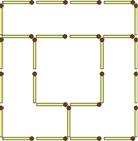
Переставьте 2 спички из 18 так, чтобы вместо 8 треугольников фигура стала состоять из 6 треугольников. Должны получиться только треугольники и не должно быть свободно висящих спичек.
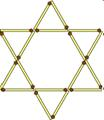 Ответ:
Ответ: 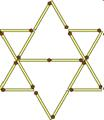
5.Задачи на логику и рассуждение
1. Определите, какие из следующих утверждений являются истинными и какие ложными.
1. Одно утверждение в этом списке ложно.
2. Две утверждения в этом списке ложны.
3. Три утверждения в этом списке ложны.
4. Четыре утверждения в этом списке ложны.
5. Пять утверждений в этом списке ложны.
6. Шесть утверждении в этом списке ложны.
7. Семь утверждений в этом списке ложны.
8. Восемь утверждений в этом списке ложны.
9. Девять утверждений в этом списке ложны.
10. Десять утверждений в этом списке ложны.
Ответ:
Все утверждения ложны, кроме девятого.
2. За книгу заплатили 100 руб. и осталось заплатить еще столько.
Сколько осталось бы заплатить, если бы за нее заплатили бы столько, сколько осталось заплатить?
Сколько стоит книга?
Ответ:
Еще столько же, всего - 200 руб.
3. Один путешественник был захвачен племенем, вождь которого решил, что тот должен умереть. Вождь был очень мудрым человеком и дал путешественнику право выбора. Путешественник должен был сказать одну фразу. Если фраза оказывалась правдивой, то его сбрасывали с высокой скалы. Если она была лживой, то путешественника должны были растерзать львы. Но путешественник сказал такую фразу, после которой его отпустили. Какую?
Ответ:
Он сказал: "Меня растерзают львы". Теперь, если бы вождь отдал его на растерзание львам, то эта фраза оказалась бы правдивой, и путешественника должны были бы сбросить со скалы. Но если его сбросят со скалы, то фраза окажется лживой. Вождь признал, что единственно правильным решением будет отпустить путешественника.
4. Цвет волос художника
В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. "Замечательно, что у одного и нас белые, у другого чёрные, а у третьего рыжие волосы, но ни у кого цвет волос не соответствует фамилии", - заметил черноволосый. "Ты прав", - сказал Белов. Какой цвет волос у художника?
Ответ:
У художника чёрный цвет волос
5. Четыре друга
Жили четыре друга. Звали их Альберт, Карл, Дитрих и Фридрих. Фамилии друзей те же, что и имена, только так, что ни у кого из них имя и фамилия не были одинаковыми, кроме того, фамилия Дитриха не Альберт. Определите фамилию и имя каждого мальчика, если известно, что имя мальчика, у которого фамилия Фридрих, есть фамилия того мальчика, имя которого - фамилия Карла.
Ответ:
Альберт Дитрих, Карл Альберт, Дитрих Фридрих, Фридрих Карл
6. Американский шпион стоял возле дверей секретного центра и смотрел на проход русских агентов. Подходит первый русский агент, ему из дверей: 26, он в ответ "13" и прошел. Подходит второй русский агент, ему: 22, он в ответ "11", и прошел. Шпион все понял и пошел ко входу, ему: 20, он в ответ "10", - шпиона арестовали. Что он должен был ответить
Ответ:
Двадцать - слово из 8 букв.
7. Мальчик, рост которого составлял один метр, вбил в дерево гвоздь точно на высоте своего роста. Три года спустя он вернулся на это место. Мальчик вырос на двадцать сантиметров, а дерево - на сорок сантиметров. Насколько теперь гвоздь оказался выше мальчика?
Ответ:
Гвоздь окажется ниже мальчика на 20 см. Деревья растут верхушкой, и поэтому гвоздь не поднимется.
8. На острове было 13 красных, 15 зеленых и 17 синих хамелеонов. Если встречаются два хамелеона разного цвета, то они одновременно меняют свой цвет на третий (например, синий и зеленый - меняются на красный).
Может ли случиться так, что через некоторое время все хамелеоны окажутся одного цвета?
Ответ:
Не могут, т.к. числа 13, 15, 17 имеют разные остатки от деления на 3.
9. Поездная бригада состоит из кондуктора, проводника, машиниста и помощника машиниста. Их зовут Андрей, Петр, Дмитрий и Трофим. Дмитрий старше Андрея.
У кондуктора нет родственников в бригаде.
Машинист и помощник машиниста — братья. Других братьев у них нет.
Дмитрий — племянник Петра.
Помощник машиниста — не дядя проводника, а проводник — не дядя машиниста.
Кто в качестве кого работает и какие родственные отношения существуют между членами бригады?
Ответ:
Так как у кондуктора нет родственников в бригаде, а Дмитрий — племянник Петра, кондуктор не может быть ни Дмитрием, ни Петром. Нетрудно также сделать вывод, что один из братьев должен быть либо Петром, либо Дмитрием. Иначе в бригаде окажутся две пары родственников, что противоречит условию: «У кондуктора нет родственников». Итак, машинист, его помощник и проводник — родственники. Разберемся в характере их связей.
Тут могут быть 2 варианта. Либо проводник Петр приходится дядей и машинисту и его помощнику, либо проводник Дмитрий является племянником одного из братьев и сыном другого. Первый вариант не годится, так как по условию проводник — не дядя машиниста. Остается второй. Учитывая, что помощник машиниста — не дядя проводника, мы можем сделать вывод, что дядей проводника является машинист. Следовательно, машиниста зовут Петром, а проводника Дмитрием. Нам известно, что Дмитрий старше Андрея. Значит, помощник машиниста Андреем быть не может (иначе сын окажется старше отца). Итак, помощник машиниста — Трофим, а кондуктор (мы пришли к этому методом исключения) — Андрей.
10. Зима. Вчера был дождь а сегодня мороз. Вечер. Вы водитель маршрутного городского автобуса. 75% заполнения салона автобуса пассажирами. Подъезжая к перекрестку затормозили. Впереди небольшая пробка. Занято две полосы вашего направления легковыми, газелями и фурами. Все буксуют по гололеду не могут тронуться. Дорожно-патрульная служба освободила одну полосу встречной для объезда. Хотели об ехать по встречке, но не тут то было, начинаете буксовать сами.
Что делать ?
Ответ:
Все пассажиры должны перейти в переднюю часть автобуса если он переднеприводной и в заднюю если заднеприводной, чтобы усилить нагрузку на ведущую ось.
6.Истинноностные задачи
1. Василиса Прекрасная
Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису?
Решение:
Начнем рассуждать с ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного. Так как украл Василису Прекрасную кто-то один, то среди ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного может быть лишь один ложный, иначе при двух ложных ответах получается, что украли ее двое.
Тогда вторым ложным ответом будет ответ Лешего, так как всего ложных ответов два. Поэтому Леший знал, кто украл Василису Прекрасную.
Ответ:
Леший знал, кто украл Василису Прекрасную.
2. Незнайка услышал разговор Сиропчика, Пилюлькина, Торопыжки и Знайки. Известно, что каждый из них либо всегда лжет, либо всегда говорит правду.
1) Сиропчик обвинил Пилюлькина в том, что он – лгун.
2) Знайка сказал Сиропчику: «Сам ты лгун!».
3) Торопыжка заметил: «Оба они лгуны».
4) Знайка спросил у Звезды «А я?».
5) На что Торопыжка ответил «И ты тоже лгун!»
«Кто же из них говорит правду?» - удивился Незнайка. Помогите ему.
Решение:
Поочередно предположим, что каждый из них говорит правду.
Допустим, что Сиропчик говорит правду. Тогда, рассмотрев первое высказывание, можно утверждать, что Пилюлькин – лгун, исходя из второго высказывания получаем, что Знайка – лгун. Третье высказывание приводит нас к противоречию: если Торопыжка говорит правду, то Сиропчик и Пилюлькин лгуны – это противоречит нашему предположению, если Торопыжка лжет, то Сиропчик и Пилюлькин говорят правду – это противоречит первому высказыванию. Приходим к выводу, что Сиропчик лжет и наше предположение не верно. Тогда Пилюлькин говорит правду.
Допустим, что Знайка говорит правду. Тогда, второе высказывание истинно и Сиропчик – лжет. Мы уже выяснили, что это правда. Рассмотрев пятое высказывание, приходим к выводу, что Торопыжка лжет.
Таким образом, Знайка и Пилюлькин говорят правду.
Ответ:
Знайка и Пилюлькин говорят правду.
3. Каждый день кот Леопольд прогуливался в городском парке. Однажды, 6 апреля кот Леопольд встретил на прогулке мышей – Серого и Белого. Леопольд забыл, когда у мышат Дни Рождения и решил спросить их об этом, чтобы вовремя подарить подарки. «Он был вчера» - ответил Серый мышонок. Белый же мышонок сказал: «Он будет завтра». На следующий день кот Леопольд опять спросил мышат об этом. «Он был вчера» - ответил Серый мышонок. «Он будет завтра» - сказал Белый. Кот Леопольд задумался над словами мышат. Он точно знал, что обманывать они могут только в день своего рождения, хоть и часто шутят над ним. Как же коту Леопольду узнать, когда дни рождения у мышат?
Решение:
Серый мышонок два дня подряд отвечал Леопольду одинаково, что день рождения был вчера. Предположим, что Серый мышонок в первый день сказал правду, следовательно, день рождения у него был 5 апреля, но учитывая, что обманывать он мог только в свой день рождения приходим к противоречию – 7 апреля мышонок не мог обмануть, а получается, что обманул. Наше предположение неверно, значит Серый мышонок обманул 6 апреля и в этот день у него день рождения.
Рассмотрим высказывания Белого мышонка. Предположим, что 6 апреля (в первый день) он сказал правду, тогда его день рождения 7 апреля и высказывание, которое Белый сказал во второй день – ложь. Следовательно, день рождения Белого мышонка 7 апреля.
Ответ:
6 апреля – у Серого мышонка, 7 апреля – у Белого мышонка.
4. Однажды на лестнице Гарри Поттер нашел странный свиток. В нем было записано сто утверждений:
«В этом свитке ровно одно неверное утверждение»
«В этом свитке ровно два неверных утверждения»
«В этом свитке ровно три неверных утверждения»
…………………………………………………………
«В этом свитке ровно сто неверных утверждений»
Есть ли среди этих утверждений верные, и если да, то какие?
Решение. То, что в свитке записано 100 утверждений, каждые два из которых противоречат друг другу, означает, что если среди них и есть верные утверждения, то их не может быть более одного. Посмотрим, может ли здесь быть хотя бы одно верное утверждение. Если верно ровно одно утверждение, то ровно девяносто девять неверных. А такое утверждение в свитке есть: «В этом свитке ровно девяносто девять неверных утверждений». Итак, в свитке записано ровно одно верное утверждение.
Ответ:
В свитке записано ровно одно верное утверждение: "В этом свитке ровно 99 неверных утверждений".
5. Коренными жителями острова являются рыцари света и рыцари тьмы. Рыцари света всегда говорят правду, а рыцари тьмы всегда лгут. Рыцарь А говорит: «Я – лжец». Является ли он уроженцем острова рыцарей света и рыцарей тьмы?
Объяснение:
Пусть Антоний сказал правду, значит, он – рыцарь тьмы. Но он не может быть рыцарем тьмы, так как рыцари тьмы всегда лгут. Пусть Антоний сказал ложь, тогда он рыцарь света. Но рыцари света говорят правду. Опять не получается. Значит, Антоний не может быть уроженцем острова рыцарей света и рыцарей тьмы.
Ответ:
Антоний не является уроженцем острова
6. В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки.
Решение
Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хаус ни рубашка ни бандана не были белыми и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета.
Получаем граф:
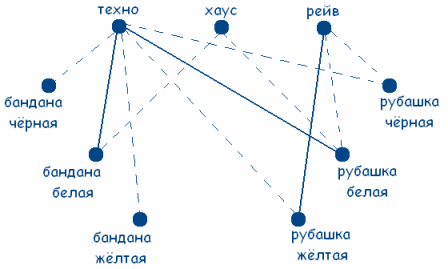
Решение сводится к нахождению трех сплошных треугольников с вершинами в разных множествах. Значит у любителя хаус желтая бандана и черная рубашка (т.к. цвет совпадал только у любителя техно по усл.), а у любителя рейв черная бандана.
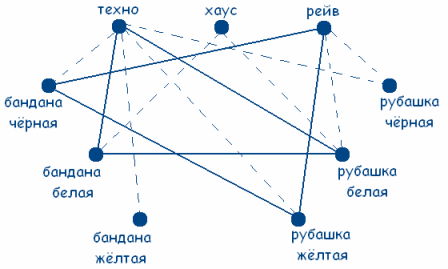
Ответ:
У любителя техно рубашка и бандана белого цвета; у любителя хаус черная рубашка и желтая бандана; у любителя рейв желтая рубашка и черная бандана.
7. Четыре футбольных команды: итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская – «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Марк. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:
а) Зенит не тренируется у Марка и Антонио.
б) Милан обещал никогда не брать Марка главным тренером.
Ответ:
Зенит - Родриго
Милан - Николай
Реал - Марк
Челси – Антонио
8.Жили-были на свете три поросенка, три брата: Ниф-Ниф, Наф-Наф, Нуф-Нуф. Построили они три домика: соломенный, деревянный и кирпичный. Все три брата выращивали возле своих домиков цветы: розы, ромашки и тюльпаны. Известно, что Ниф-Ниф живет не в соломенном домике, а Наф-Наф – не в деревянном; возле соломенного домика растут не розы, а тот, у кого деревянный домик, выращивает ромашки. У Наф-Наф аллергия на тюльпаны, поэтому он не выращивает их. Узнайте, кто в каком домике живет и какие цветы выращивает.
Ответ:
Наф-Наф живет в кирпичном домике и выращивает розы; Ниф-Ниф живет в деревянном домике и выращивает ромашки; Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
9. В компьютерном классе на уроке информатики, во время отсутствия учителя, пять ребят – Максим, Настя, Саша, Рома, Сережа – отвлеклись от нужной работы и стали играть в такие игры: пасьянс «Паук», гонки, сапер, «Марио», тетрис. Каждый из них играл только в одну игру.
• Саша думал, что в «Марио» играет Настя.
• Настя предполагала, что Рома играет в тетрис, а Максим – в гонки.
• Рома считал, что Сережа играет в гонки, а Саша – в сапера.
• Максим думал, что Настя раскладывает пасьянс «Паук», а в «Марио» играет Рома.
В результате оказалось, что все они ошиблись в своих предположениях. Кто и во что играл?
Решение:
Таблица с известными запретами (исходя из условия задачи):
| Имя | Максим | Настя | Саша | Рома | Сережа |
| Игра |
| Пасьянс «Паук» | - | - | | | |
| Гонки | - | - | | - | - |
| Сапер | | | - | - | |
| «Марио» | - | - | - | - | |
| тетрис | | - | | - | |
Известно, что каждый из игравших играл только в одну, значит, в каждой строке и каждом столбце таблицы может стоять только один «+».
Из условий задачи следует, что Саша не играл в «Марио»; Настя не играла ни в тетрис, ни в гонки; Рома – ни в гонки, ни в сапера; Максим – ни в пасьянс «Паук», ни в Марио.
Так как все предположения ошибочны, то Настя не играет в «Марио», Рома – в тетрис, Максим – в гонки, Сережа – в гонки, Саша – в сапера, Настя – в пасьянс «Паук», Рома – в «Марио».
Используем правило, что если в строке (или столбце) все места, кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+». В строчке «гонки» можно поставить «+» напротив имени Саша, а в строчке «Марио» напротив имени Сережа. Получаем:
| Имя | Максим | Настя | Саша | Рома | Сережа |
| Игра |
| Пасьянс «Паук» | - | - | - | | - |
| Гонки | - | - | + | - | - |
| Сапер | | | - | - | - |
| «Марио» | - | - | - | - | + |
| тетрис | | - | - | - | - |
Теперь становится ясно, что в пасьянс «Паук» играл Рома, в сапера – Настя, а в тетрис – Максим. Задача решена.
Ответ:
Сережа играл в «Марио»; Рома – в пасьянс «Паук»; Саша – в гонки; Настя – в сапера; Максим – в тетрис.
10. Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее:
• Атос и Арамис наблюдали на балу за их другом – прекрасным танцором.
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника.
• Стрелок хочет пригласить в гости Атоса.
• Портос был очень большой комплекции, поэтому танцы были не его стихией.
Кто чем занимается?
Решение:
Таблица с известными запретами:
| Занятие | шпажист | рукопашник | танцор | стрелок |
| Имя |
| Атос | | | - | - |
| Портос | | - | - | - |
| Арамис | | | - | |
| Д’Артаньян | | | | |
Известно, что каждый из четырех мушкетеров был лучшим только в одном деле. Следовательно, в каждой строчке и каждом столбце может стоять только один «+». Взглянув на таблицу, сразу можно сказать, что танцор – Д’Артаньян, шпажист – Портос. Вносим эти данные в таблицу. Получаем:
| Занятие | шпажист | рукопашник | танцор | стрелок |
| Имя |
| Атос | - | | - | - |
| Портос | + | - | - | - |
| Арамис | - | | - | |
| Д’Артаньян | - | - | + | - |
Теперь можно сделать вывод, что стрелок – это Арамис, рукопашник – Атос.
Ответ:
Арамис – стрелок; Д’Артаньян – танцор; Портос – шпажист; Атос – рукопашник.














 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 























