Учебный проект - реферат "Геометрия бордюров"

Муниципальное образовательное учреждение

«Торбеевская основная общеобразовательная школа имени А.И.Данилова»

реферат

ученицы 8 класса

Мыслиной Светланы

2011

Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математики.

Г.Вейль

изучить законы конструирования бордюров, выяснить, какие математические принципы лежат в основе познания и создания бордюров

• Изучить литературу, Интернет-источники по теме;

• Собрать подборку образцов бордюров;
• Создать самой образцы бордюров разных видов;
• С результатами своей работы познакомить

учащимися школы

Бордюр – это периодически повторяющийся рисунок на длинной ленте

С точки зрения математики рисунок на длинной ленте можно отнести к бордюрам в том случае, если он получается из некоторого элемента путем геометрических перемещений, которые переводят данную ленту и некоторую прямую на ней в себя. Точки этой прямой могут и не оставаться неподвижными, главное, чтобы эта прямая переходила в себя.

Математик, так же как художник или поэт, создаёт узоры.

Г. Харди.

• параллельный перенос;
• зеркальная симметрия с вертикальной осью;
• зеркальная симметрия с горизонтальной осью;
• центральная симметрия.

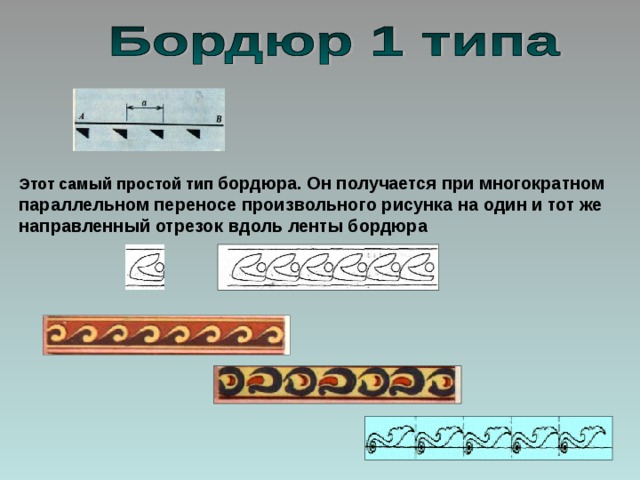
Этот самый простой тип бордюра. Он получается при многократном параллельном переносе произвольного рисунка на один и тот же направленный отрезок вдоль ленты бордюра

Прямая a на этом рисунке является осью симметрии бордюра. Чтобы получить бордюр этого типа, нужно взять произвольный рисунок, отразить его относительно прямой, объединить с данным, а затем полученный рисунок смещать параллельным переносом вдоль ленты бордюра.

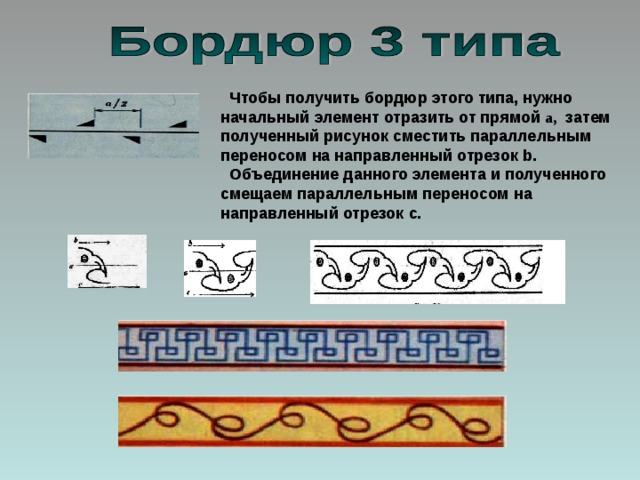
Чтобы получить бордюр этого типа, нужно начальный элемент отразить от прямой а, затем полученный рисунок сместить параллельным переносом на направленный отрезок b .

Объединение данного элемента и полученного смещаем параллельным переносом на направленный отрезок с.

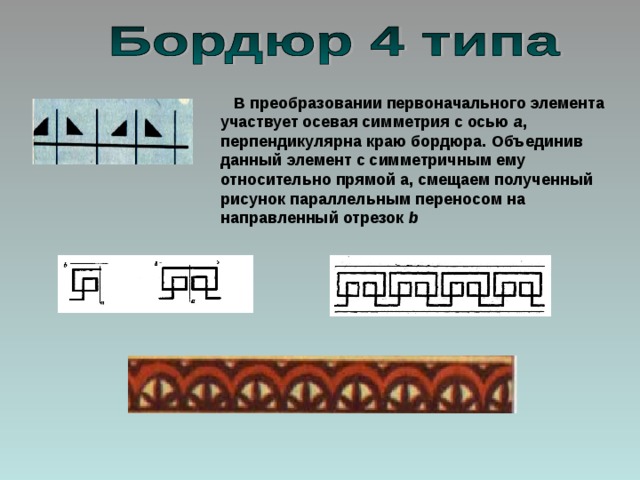
В преобразовании первоначального элемента участвует осевая симметрия с осью а , перпендикулярна краю бордюра. Объединив данный элемент с симметричным ему относительно прямой а, смещаем полученный рисунок параллельным переносом на направленный отрезок b

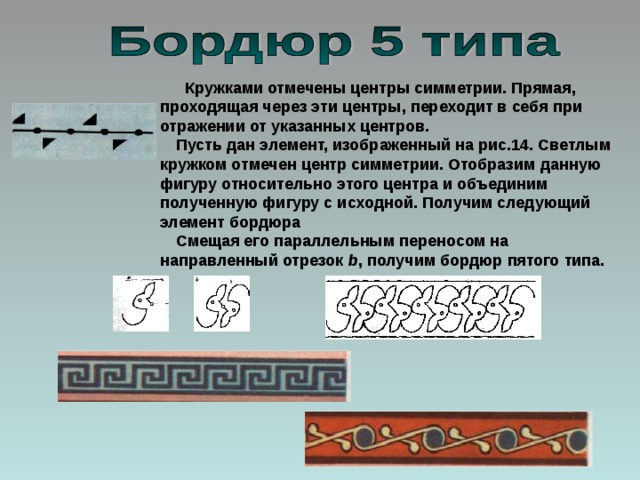
Кружками отмечены центры симметрии. Прямая, проходящая через эти центры, переходит в себя при отражении от указанных центров.

Пусть дан элемент, изображенный на рис.14. Светлым кружком отмечен центр симметрии. Отобразим данную фигуру относительно этого центра и объединим полученную фигуру с исходной. Получим следующий элемент бордюра

Смещая его параллельным переносом на направленный отрезок b , получим бордюр пятого типа.

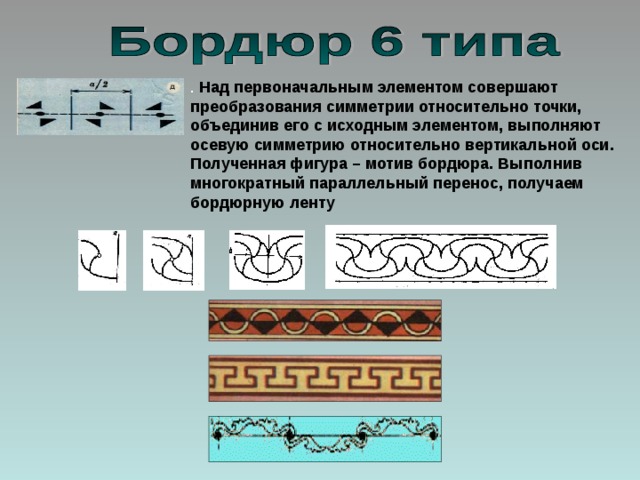
. Над первоначальным элементом совершают преобразования симметрии относительно точки, объединив его с исходным элементом, выполняют осевую симметрию относительно вертикальной оси. Полученная фигура – мотив бордюра. Выполнив многократный параллельный перенос, получаем бордюрную ленту

Над первоначальным элементом совершают преобразования симметрии относительно горизонтальной прямой. Объединив его с исходным элементом, выполняют осевую симметрию относительно вертикальной оси. Полученная фигура – мотив бордюра. Выполнив многократный параллельный перенос, получаем бордюрную ленту.

Выцинаньки – это особенным образом вырезанные из тонкой цветной бумаги бордюры. Ими украшали стены в доме, окна, дверцы шкафчиков.

Бумагу для выцинаньки складывают несколько раз гармошкой, прорезают узор сразу по всем слоям, не трогая сгибов, и разворачивают. Получается повторяющийся в полосе орнамент – бордюр.

Геометрия – не только стройная система теорем и аксиом, но и уникальное средство познания и создания красоты.

Изучая геометрию, мы приближаемся

к пониманию прекрасного .