Метод учебных проектов

МОУ «ЛИЦЕЙ № 12»

Учебный проект

"СТЕПЕННЫЕ ФУНКЦИИ,

их свойства и графики"

Выполнили:

учащиеся 11 класса

Руководитель:

Каримова Елена Викторовна

г. Железногорск

Цели и задачи:

• Изучить свойства и особенности

графиков степенных функций , где r – рациональное число.

• Рассмотреть примеры практического применения изученных свойств функций.
• Показать использование степенных функций в окружающей жизни.

Степенными функциями называют функции вида , где r – любое рациональное число

О происхождении терминов и обозначений

• К умножению равных сомножителей приводит решение многих задач. Понятие степени с натуральным показателем возникло уже в Древней Греции (выражение квадрат числа возникло при вычислении площади квадрата, а куб числа – при нахождении объема куба). Но современные обозначения (типа

) в XVII в. ввел Декарт.

• Дробные показатели степени и наиболее простые правила действий над степенями с дробным показателем встречаются в XIV в. у французского математика Н. Орема (1323 -1382). Известно, что Шюке (ок. 1445 - ок. 1500) рассматривал степени с отрицательным и нулевым показателем.
• С.Стевин предложил подразумевать под корень .
• Немецкий математик М. Штифель (1487-1567) дал определение

при и ввел название показатель (это буквенный перевод с немецкого Exponent). Немецкое potenzieren означает возведение в степень .

• Но систематически рациональные показатели первым стал употреблять Ньютон (1643 -1727).

Симон Стевин

Николай Оре́м,

(1548-1620)

или Николай Орезмский

(1323-1382)

Рене Декарт

(1596-1650)

«Как алгебраисты вместо АА, ААА, … пишут А 2 , А 3 , …,

так я вместо пишу а -1 , а -2 , а - 3 , … »

Ньютон И.

(1643 -1727)

Степенная функция у=х , где - целое число

m

m

y

у = х

1

0

1

x

y

у = х 2

у = х 4

у = х 6

1

1

x

0

y

у = х 3

у = х 5

у = х 7

1

1

x

0

y

у = х -1

у = х -3

у = х -5

1

x

0

y

у = х -4

1

1

x

0

« Степенная функция

где »

у = х 2,5

у

у = х 3,1

у = х 1,5

- 1 0 1 2

x

Свойства функции

• ;
• не является ни четной, ни нечетной;
• возрастает на ;
• не ограничена сверху, ограничена снизу;
• не имеет наибольшего значения; ;
• непрерывна;
• ;
• выпукла вниз;

Докажем третье свойство :

Пусть

Тогда

, т.е.

следует

Итак, из

т.е. функция возрастает на

Выводы:

• Особенности графика функции , где

: расположен в I координатной четверти, проходит через точки (0;0), (1;1), похож на «ветвь» параболы.

Степенные функции

их свойства и графики

y

Функция

у = х 0,84

у = х 0,7

у = х 0,5

- 1 0 1 2

x

Выводы:

• Особенности графика функции , где

: расположен в I координатной четверти, проходит через точки (0;0), (1;1), похож на график функции , обладает такими же свойствами.

Степенные функции

их свойства и графики

y

Функция

у = х -2,3

у = х -3,8

у = х -1,3

у = х -0,3

- 1 0 1 2

x

Выводы:

• Особенности графика функции :

расположен в I координатной четверти,

проходит через точки (0;0), (1;1),

похож на «ветвь» гиперболы.

График данной функции имеет горизонтальную

асимптоту у = 0 и вертикальную асимптоту х = 0.

2. Практическое применение

1. Решите уравнение

Решение.

• Нетрудно подобрать один корень этого уравнения:

х = 1.

– верное равенство.

2) Т.к. степенная функция

возрастает, а линейная

функция

убывает, то других корней у

уравнения нет.

Ответ : х =1.

2. Найдите наименьшее и наибольшее значения функции

на отрезке [1;2].

Решение:

Воспользуемся тем, что функция возрастает и, следовательно, свои наименьшее и наибольшее значения достигает соответственно в левом и правом концах заданного промежутка, если концы промежутка принадлежат самому промежутку.

y

Задание. Построить график функции

3

Y=(X-2)-1

1

0 1

x

Пример

у = (х+2) –1,3 +1

у = х -1,3

- 1 0 1 2

x

Задания для самостоятельного решения

• Решите уравнение .

• Постройте и прочитайте график функции

• Решите неравенство .

Функции

в пословицах

«Долго думал, да ничего не выдумал»

Идеи, придумки, задумки

y

x, время (час)

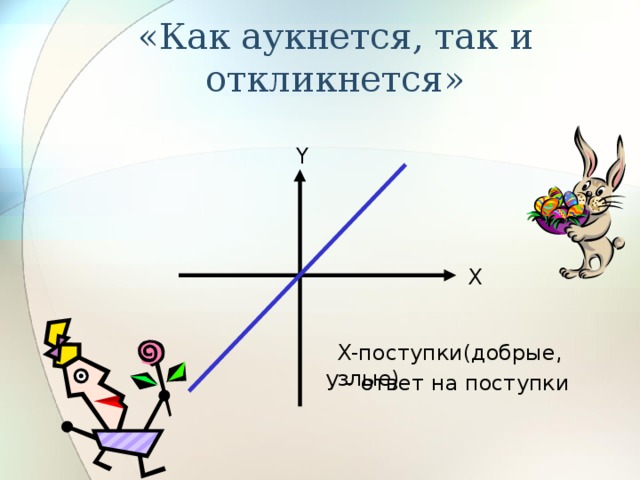
«Как аукнется, так и откликнется»

Y

X

Х-поступки(добрые, злые)

У - ответ на поступки

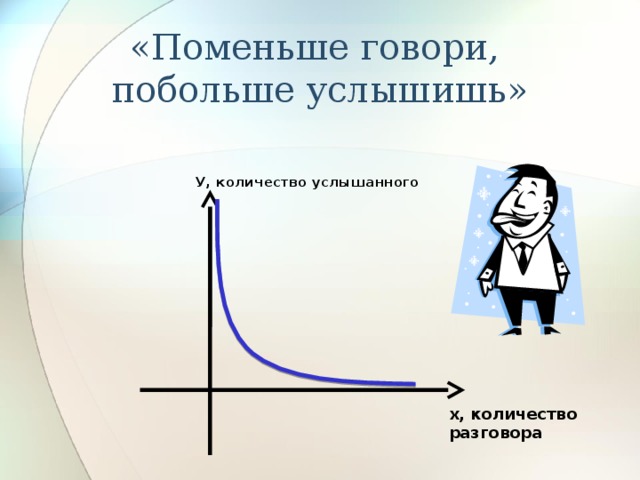
«Поменьше говори, побольше услышишь»

У, количество услышанного

х, количество разговора

Применение

функций

Применение степенной функции в физике

• , где S - площадь

поперечного сечения провода диаметра d

H

• F=Qm 1 m 2 r -2 , где F - сила притяжения между двумя телами с массами m 1 и m 2 , находящихся на расстоянии r, Q- постоянная гравитационная величина

Траектория движения тела, брошенного вверх

м

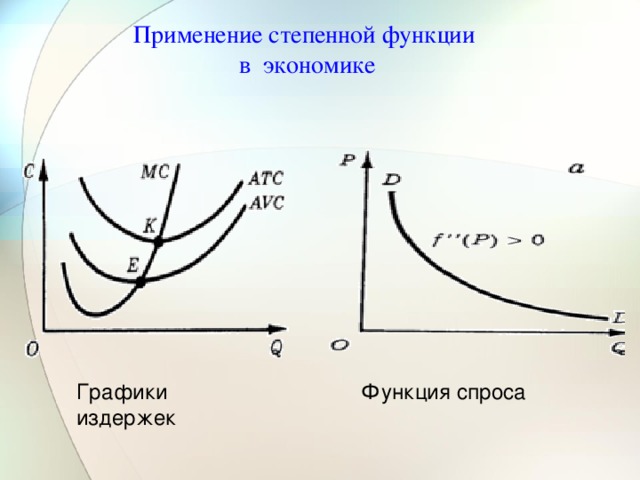
Применение степенной функции

в экономике

Функция спроса

Графики издержек

3. Степенные функции в окружающей

жизни. Гиперболоиды вращения

• Вращая гиперболу вокруг каждой из этих осей, получают два гиперболоида вращения -однополостной и двуполостной.

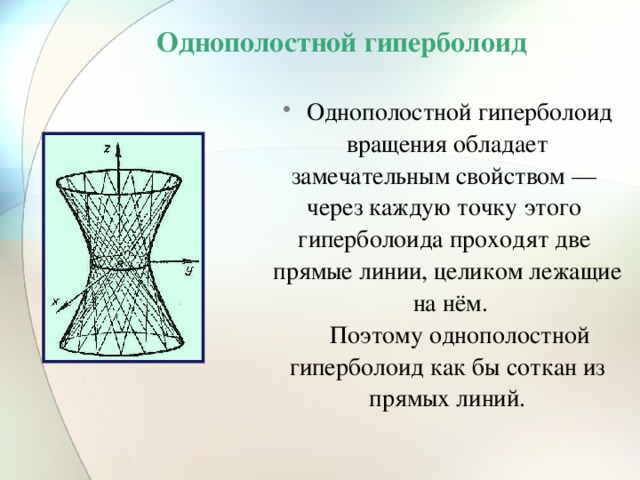
Однополостной гиперболоид

• Однополостной гиперболоид

вращения обладает

замечательным свойством —

через каждую точку этого

гиперболоида проходят две

прямые линии, целиком лежащие

на нём.

Поэтому однополостной

гиперболоид как бы соткан из

прямых линий.

Применение гиперболоидов

• Свойства однополостного гиперболоида использовал русский инженер В.Г. Шухов при строительстве радиостанции в Москве (башни Шухова). Она состоит из нескольких

поставленных друг на друга однополостных гиперболоидов.

• Также устроена и Эйфелева башня в Париже.

Параболоид вращения

Пусть парабола начнет вращаться вокруг оси ординат. Получится что-то вроде чаши, только, чтобы она не была бесконечной, отрежем часть ее плоскостью, перпендикулярной оси ординат. Образуется фигура, которая называется параболоидом.

При вращении тонкого прямоугольного сосуда с жидкостью вокруг его горизонтального центра поверхность жидкости в сосуде принимает форму параболы

Свойство параболы о фокусировании параллельного пучка прямых используется в конструкции прожекторов, фонарей, фар, а так же телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Если теперь сделать внутреннюю поверхность параболоида зеркальной и направить поток света по направлению оси ординат, то все лучи света соберутся в одной точке, которую, называют фокусом. А если в фокус поставить источник света, например, электрическую лампочку, то получится самая обыкновенная фара, или прожектор, или часть карманного фонарика.

Одно из очень важных применений параболы на практике связано с антенными устройствами.

Траектория движения - парабола

Парабола вокруг нас

Перевал Нижняя Парабола

Парабола в архитектуре и строительстве

Выводы:

• Рассмотренные свойства функций можно применить на практике при решении уравнений, неравенств, систем уравнений и неравенств.
• Степенные функции находят широкое применение в окружающей жизни, в смежных дисциплинах.