Углы и отрезки, связанные с окружностью

Углы и отрезки, связанные с окружностью

Решение задач

№ 816

B

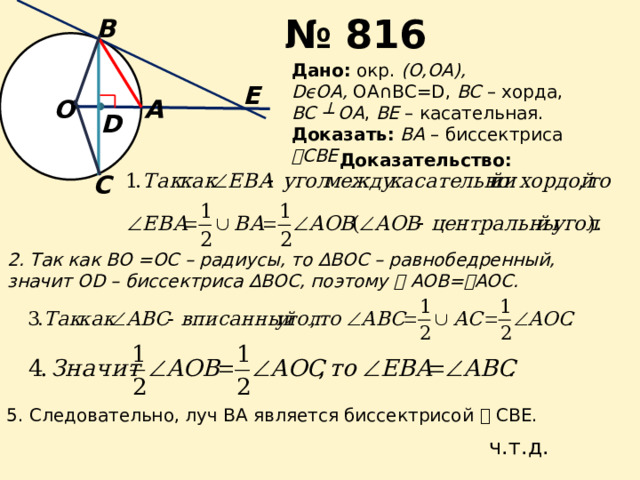
Дано: окр. (О,ОА),

DϵOA, OA∩BC=D, ВС – хорда,

ВС ┴ ОА , ВЕ – касательная.

Доказать: ВА – биссектриса ے СВЕ

E

А

О

D

Доказательство:

C

2. Так как ВО =ОС – радиусы, то ∆ВОС – равнобедренный,

значит OD – биссектриса ∆ВОС, поэтому ے АОВ= ے АОС.

5. Следовательно, луч ВА является биссектрисой ے СВЕ.

ч.т.д.

К

№ 817

А

В₁

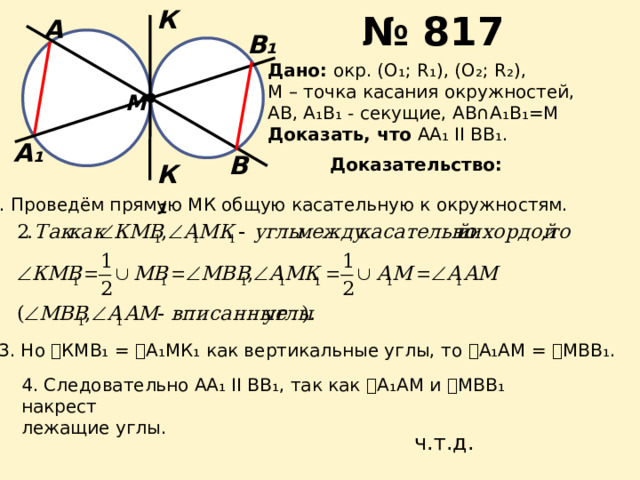
Дано: окр. (О₁; R₁), (O₂; R₂),

М – точка касания окружностей,

АВ, А₁В₁ - секущие, АВ∩А₁В₁=М

Доказать, что АА₁ II ВВ₁.

М

А₁

В

Доказательство:

К₁

1. Проведём прямую МК общую касательную к окружностям.

3. Но ے КМВ₁ = ے А₁МК₁ как вертикальные углы, то ے А₁АМ = ے МВВ₁.

4. Следовательно АА₁ II ВВ₁, так как ے А₁АМ и ے МВВ₁ накрест

лежащие углы.

ч.т.д.

№ 818 рис. 208

Дано: АС – касательная к окр. (О₁; R₁), BD – касательная к окр. (О₂; R₂)

Доказать, что а) AD II BC; б) AB² = AD · BC; в) BD² : AC² = AD : BC.

Доказательство:

б) 3) ∆ABD ̴ ∆ABC по I признаку подобия треугольников, то

ч.т.д.

№ 819

Дано: ABCD – четырёхугольник, М ϵ (ABCD),

М – точка окружностей описанных около

∆ АВМ и ∆CDM, (ABM) ∩ (CDM) = M.

Доказать, что ے AMD = ے ABM + ے MCD.

Доказательство:

К

1). Проведём через точку М касательную к окружности, описанной около ∆АВМ.

4). Следовательно КМ является касательной к окружности, описанной около ∆MCD.

5). Поэтому ے AMD = ے AMK + ے KMD = ے ABM + ے MCD.

ч.т.д.

№ 820

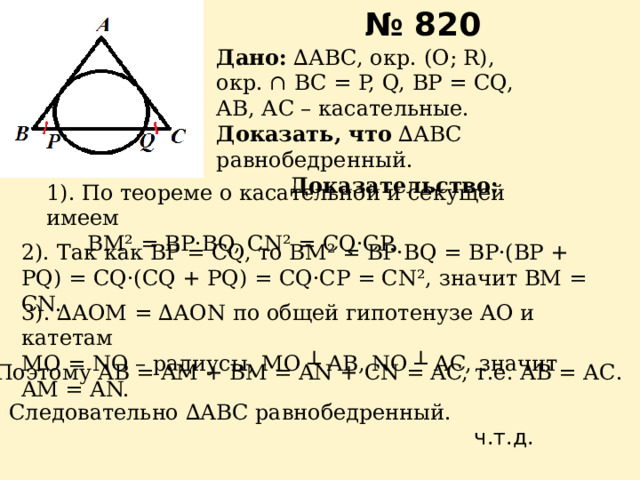
Дано: ∆АВС, окр. (О; R),

окр. ∩ BC = P, Q, BP = CQ,

АВ, АС – касательные.

Доказать, что ∆АВС равнобедренный.

Доказательство:

N

M

O

1). По теореме о касательной и секущей имеем

ВМ² = ВР·BQ, CN² = CQ·CP.

2). Так как BP = CQ, то BM² = BP·BQ = BP·(BP + PQ) = CQ·(CQ + PQ) = CQ·CP = CN², значит ВМ = СN.

3). ∆АОМ = ∆АОN по общей гипотенузе АО и катетам

MO = NO – радиусы, MO ┴ AB, NO ┴ AC, значит AM = AN.

4). Поэтому AB = AM + BM = AN + CN = AC, т.е. АВ = АС.

5). Следовательно ∆АВС равнобедренный.

ч.т.д.

№ 821

Дано: окр. (О; R), AB ∩ CD = E,

AB = CD – хорды.

Доказать, что EC = EB или EC = EA, ED = EB или ED = EA.

Доказательство:

1). По теореме о пересечения хорд имеем AE · EB = CE · DE.

2). Так как хорды AB = CD, то выразим DE через AB,

DE = AE + EB – CE, AE · EB = CE · (AE + EB – CE),

AE·EB = CE·AE + CE·EB – CE²,

AE·EB – CE·AE – CE·EB + CE² = 0,

AE·(EB – CE) – CE·(EB – CE) = 0, (EB – CE)·(AE – CE) = 0.

3). Значит либо EB – CE = 0 или либо AE – CE = 0.

4). Следовательно EB = CE или AE = CE, тогда EB = ED или EA = ED.

ч.т.д.

№ 822

Дано: окр. (О; R), КА – хорда,

КВ – касательная, ОN ﬩ OA,

ON ∩ KA = M, OM ∩ KB = N.

Доказать, что NK = NM.

Доказательство:

1). Так как ОК- радиус, КВ – касательная, то ОК ﬩ КВ и КА ∩ ON = M, значит ے NKM = 90 ° - ے AKO.

2). ∆АОМ – равнобедренный (ОА = ОК – радиусы), то ے ОКА = ے ОАК.

3). ∆АОМ, ے АОМ = 90 °, (ON ﬩ OA) , то ے АМО = 90 ° – ے МАО.

4). Значит ے NKM = ے AMO.

5). Но ے АМО = ے NMK как вертикальные углы, значит ے NKM = ے NMK.

6). Следовательно ∆KMN равнобедренный, а значит NK = NM.

ч.т.д.

№ 823 рис. 209

Дано: окр. (О; R), АВ, АС, В ₁ С ₁ - хорды, АВ ∩ В ₁ С ₁ = М,

АС ∩ В ₁ С ₁ = N, ᴗАВ ₁ = ᴗ В ₁ В, ᴗ АС ₁ = ᴗ С ₁ С.

Доказать, что AM =AN.

Доказательство:

2). Но ᴗАВ ₁ = ᴗ В ₁ В и ᴗ АС ₁ = ᴗ С ₁ С, значит ے АМС ₁ = ے ANB ₁ .

3). Следовательно ∆AMN равнобедренный, поэтому AM =AN.

ч.т.д.

№ 824

Дано: окр. (О; R), А, В, С, D ϵ окр.,

ВМ – биссектриса ∆АВС, ВМ ϵ BD.

Доказать, что ے AMD = ے BAD.

Доказательство:

1). Так как ВМ – биссектриса ∆АВС, то ے АВМ = ے МВС.

2). Так как вписанные углы ے DBC и ے DAC опираются на одну и ту же ᴗ СD, то ے DВC = ے DAС.

3). Следовательно ے АВМ = ے МВС = ے DAС.

4). Из теоремы о сумме углов ∆АMD и ∆ABD, имеем ے AMD = 180 ° - ے DAМ – ے МDA, ے BAD = 180 ° –

– ے ABD – ے BDA, т.е. ے BAD = 180 ° – ے DAM – ے MDA.

5). Следовательно ے AMD = ے BAD.

ч.т.д.

№ 826

К

Дано: ∆АВС, АА ₁ , ВВ ₁ – высоты.

Доказать, что А, В, А ₁ , В ₁ ϵ окр. (О; R).

Доказательство:

1). Возьмем точку К ϵ АВ, так что АК = КВ.

2). Так как ∆АВВ ₁ , ے В ₁ = 90 ° , то КВ ₁ = КА = КВ.

3). Так как у прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы, т.е. в точке К, то точки А, В, В ₁ ϵ окр. (К; КВ ₁).

4). Так как ∆АВА₁, ے А ₁ = 90 ° , то КА ₁ = КА = КВ.

5). Значит точки А, В, А ₁ ϵ окр. (К; КА ₁).

6). Следовательно точки А, В, А ₁ , В ₁ ϵ окр. (К; КВ ).

ч.т.д.

№ 827

Дано: АВСD – вписанный четырёхугольник, АС ﬩ ВD – диагонали.

Доказать, что AB² + CD² = BC² + AD² = d².

Доказательство:

1). Обозначим ے CAD = φ, тогда ے ADB = 90° – φ.

3). Выразим и сложим АВ = 2Rcos φ , CD = 2Rsin φ, тогда AB² + CD² = 4R².

4). По теореме Пифагора из треугольников имеем AB² + CD² = (BK² + AK²) + (CK² + DK²) = (BK² + CK²) + (AK² + DK²) = BC² + AD² = 4R² = d².

ч.т.д.