Углы. Подготовка к ОГЭ, задание №16

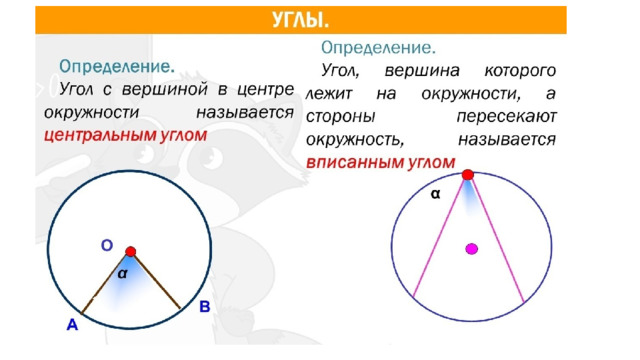
Углы

Подготовка к ОГЭ

Задание 16

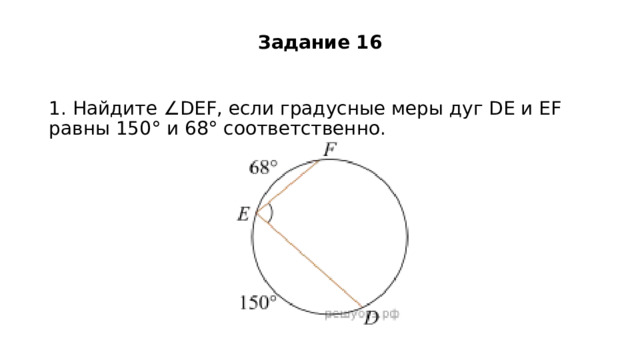
Задание 16

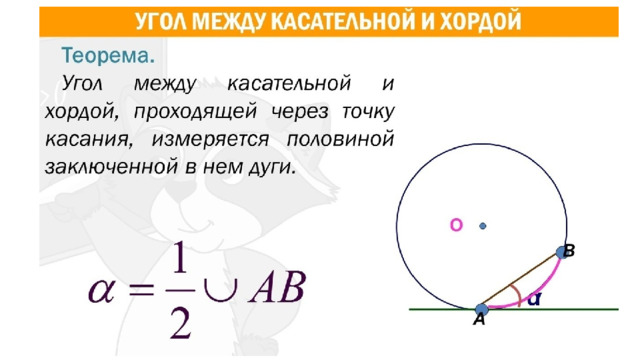
1. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

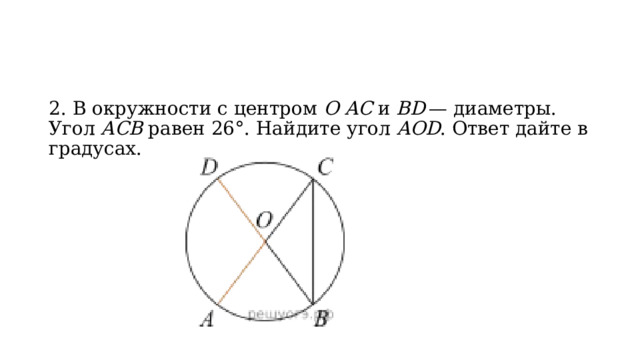
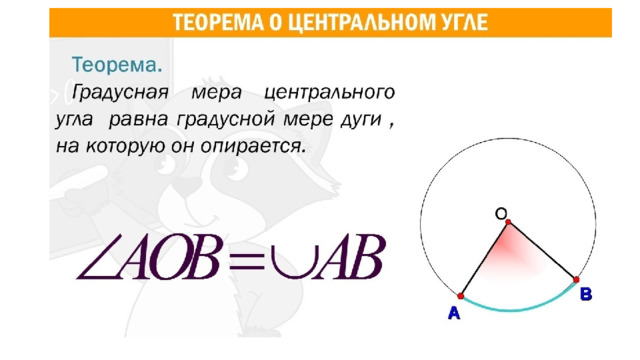
2. В окружности с центром  O AC  и  BD  — диаметры. Угол  ACB  равен 26°. Найдите угол  AOD . Ответ дайте в градусах.

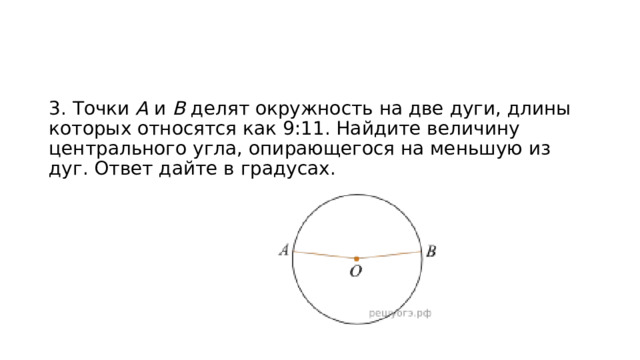
3. Точки  A  и  B  делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.

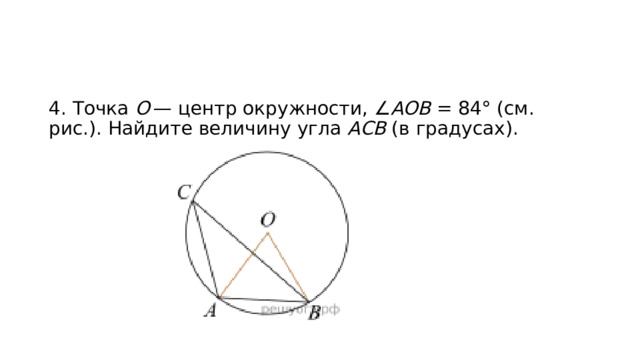
4. Точка  О  — центр окружности, ∠ AOB  = 84° (см. рис.). Найдите величину угла  ACB  (в градусах).

5. Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.

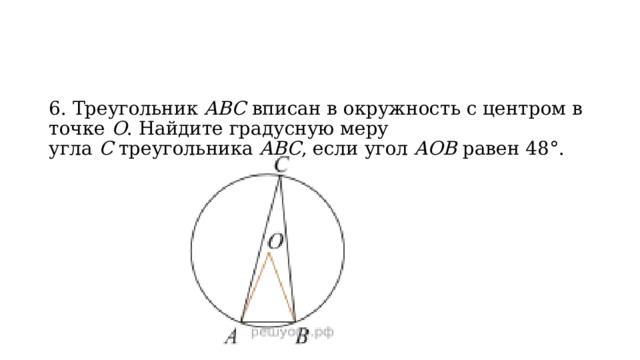
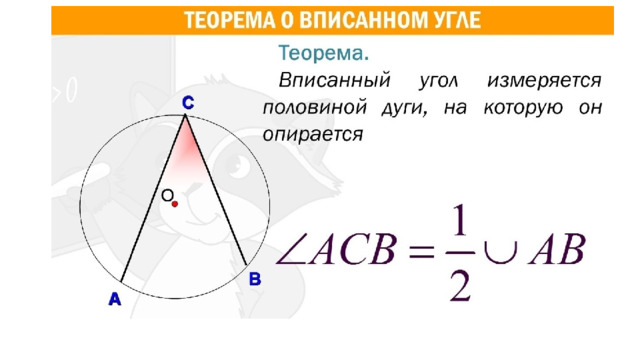
6. Треугольник  ABC  вписан в окружность с центром в точке  O . Найдите градусную меру угла  C  треугольника  ABC , если угол  AOB  равен 48°.

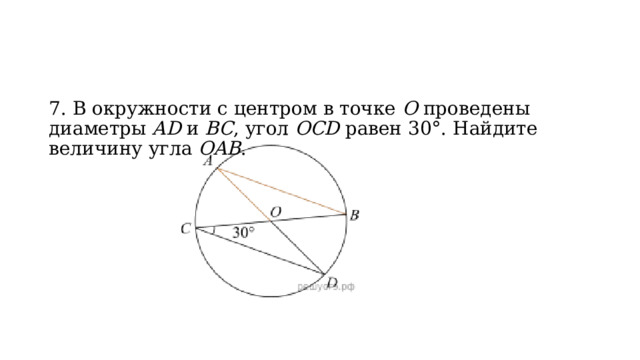
7. В окружности с центром в точке  О  проведены диаметры  AD  и  BC , угол  OCD  равен 30°. Найдите величину угла  OAB .

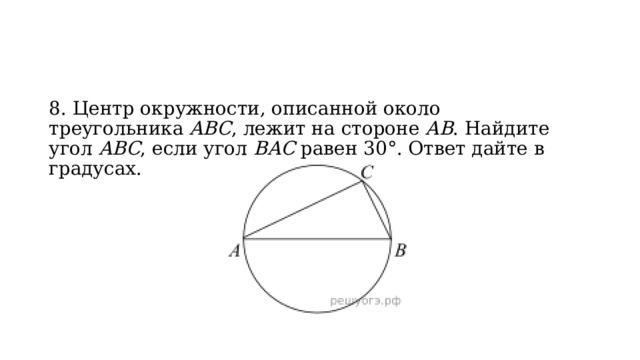
8. Центр окружности, описанной около треугольника  ABC , лежит на стороне  AB . Найдите угол  ABC , если угол  BAC  равен 30°. Ответ дайте в градусах.

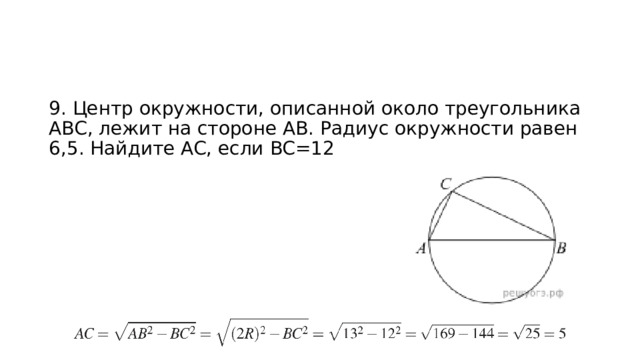
9. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 6,5. Найдите AC, если BC=12

10. На окружности отмечены точки  A  и  B  так, что меньшая дуга  AB  равна 72°. Прямая  BC  касается окружности в точке  B  так, что угол  ABC  острый. Найдите угол  ABC . Ответ дайте в градусах.

• Таким образом, поскольку

угол  OBC  прямой, угол  ABC  

равен 90° − 54° = 36°.

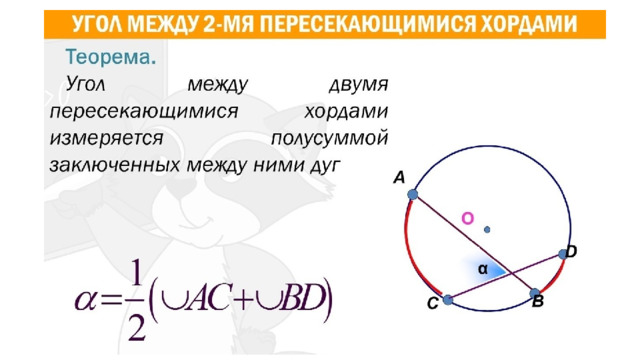
11. Прямая касается окружности в точке  K . Точка  O  — центр окружности. Хорда  KM  образует с касательной угол, равный 83°. Найдите величину угла  OMK . Ответ дайте в градусах.

• Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги  MK  равна 2 · 83° = 166°. Угол  MOK  — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол  MOK  равен 166°. В треугольнике  OMK  стороны  OK  и  OM  равны как радиусы окружности, поэтому треугольник  OMK  — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠ OKM  = ∠ OMK  = (180° − ∠ KOM )/2 = (180° − 166°)/2 = 7°.
•  
• Ответ: 7.

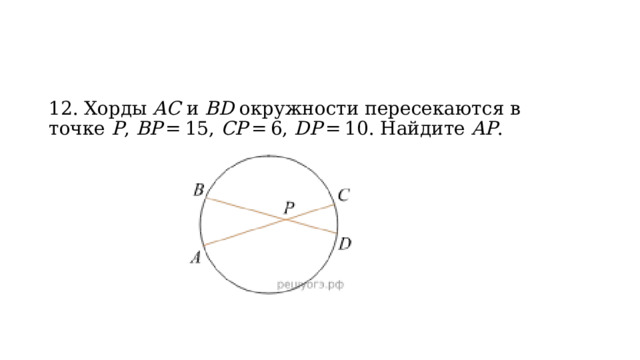
12. Хорды  AC  и  BD  окружности пересекаются в точке  P ,  BP  = 15,  CP  = 6,  DP  = 10. Найдите  AP .

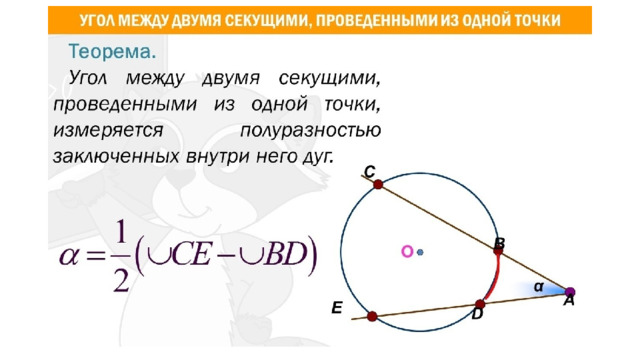
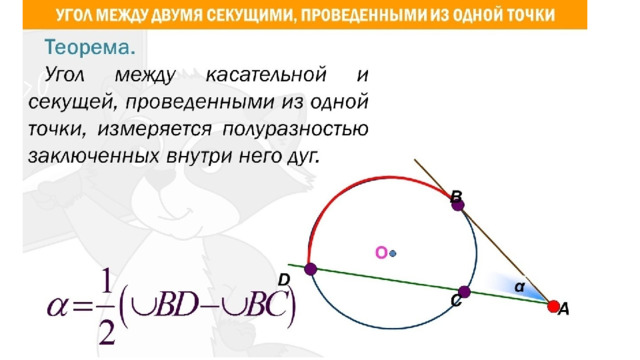
13. Через точку  A , лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке  K . Другая прямая пересекает окружность в точках  B  и  C , причём  AB  = 2,  AC  = 8. Найдите  AK .

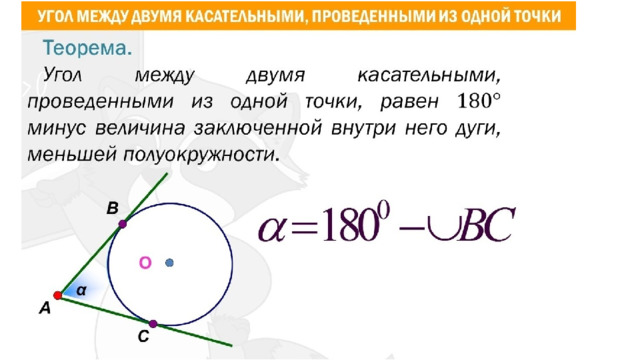
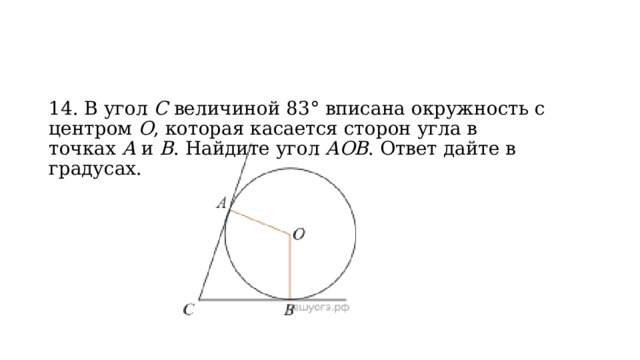
14. В угол  C  величиной 83° вписана окружность с центром  O , которая касается сторон угла в точках  A  и  B . Найдите угол  AOB . Ответ дайте в градусах.

15. В угол  C  величиной 157° вписана окружность, которая касается сторон угла в точках  A  и  B , точка  O  — центр окружности. Найдите угол  AOB . Ответ дайте в градусах.

16. В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.

• Ответ: 55.

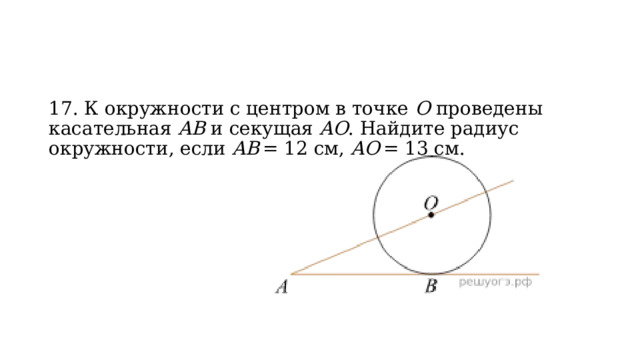
17. К окружности с центром в точке  О  проведены касательная  AB  и секущая  AO . Найдите радиус окружности, если  AB  = 12 см,  AO  = 13 см.