Учитель математики: Гасраталиева Расинат Магомедовна
Открытый урок в 7 а классе
« Умножение разности двух выражений на их сумму»
Цели:1.вывести формулу умножения разности двух выражений на их сумму, сформулировать правило, выработать умение применять формул
2.развивать умение анализировать, сравнивать, делать умозаключения
3.прдолжать воспитание устойчивого интереса к математике
Ход урока
1.Организационный момент.
Чтобы легче всем жилось
Чтоб решалось, чтоб моглось,
Улыбнись, удача всем,
Чтобы не было проблем.
-Улыбнулись друг другу, создали хорошее настроение и начали урок.
2.Актуализация знаний.
1.Проверка домашнего задания.
-Сегодня мы продолжаем тему «Тождества сокращенного умножения»
Проверка усвоения формул сокращенного умножения.
2.Вставить пропущенные слова в формулировки формул.
Квадрат суммы двух выражений равен ______ первого выражения ______ удвоенное произведение ______ и ______ выражений ______ второго выражения.
Напишите формулу квадрата суммы двух выражений ______.
Квадрат разности двух выражений равен ______ первого выражения ______ удвоенное произведение ______ и ______ выражения ______ второго выражения.
Напишите формулу квадрата разности двух выражений ______
3.Устный счет. а).Верны ли утверждения?
б)Возвести в квадрат.
4.Работа над новым материалом.
Мы с вами научились умножать сумму двух выражений на такую же сумму и разность на такую же разность, причем умножаем «сокращенно», используя формулы. А как вы думаете, есть еще формулы сокращенного умножения?(Да)
-Так какую же цель мы сегодня поставим перед собой? (Открыть еще формулы)
-Какие предложения будут?(Умножить разность двух выражений на их сумму)
а) Класс делится на группы. Задания на доске. Каждой группе по 2 выражения: умножить многочлен на многочлен.
1)(а-в)(а+в)=
2)(х-у)(х+у)=
3)(р-5)(р+5)=
4)(х+3)(х-3)=
5)(m-n)(m+n)=
6)(p+q)(p-q)=
Ученики на местах решают, потом старшие в группе выходят и записывают ответы на доске.
- Запишите в тетрадях число, тему вы мне назовете позже.
Что интересного вы замечаете? (Во всех случаях получилось одно и тоже выражение – разность квадратов данных выражений.) Запишем формулу, которую получили:
(а-в)(а+в)=а2-в2
- Сформулируйте правило, по которому можно найти произведение разности и суммы двух выражений. Как записать правило в общем виде?
(∆ - 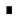 )(∆ +
)(∆ + 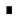 )=
)=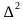 -
- 
-Работа с книгой: стр.161Прочитать правило. Рассказать правило соседу
–– Достигли мы поставленных целей? (Частично, т.к. вывели формулу.) Что теперь предстоит сделать? (Научиться использовать эту формулу для преобразования выражений.)
- Рассмотрим примеры. (Примеры записаны на доске слева. Решение на доске записывает учитель, учащиеся делают записи в тетрадях.)
1) (2х-3)(2х+3)=(2х)2-32=4х2-9;
2) (х3+7)(х3-7)=... Можно ли сказать, что дано произведение разности и суммы двух выражений? (Да. Множители в произведении можно менять местами.)...=(х3)2-72=х6-49.
3) (3у4+5)(5-3у4)=.. Верно ли, что в данном выражении есть произведение разности и суммы двух выражений? (Да, если поменять местами множители и слагаемые в сумме.)...= =(5-3у4)( 5+3у4)=52-(3у4)2=25-9у8.
- Какие практические советы можно сформулировать при работе с формулой? Каков алгоритм работы с формулой? (Записать квадрат первого выражения, поставить минус, записать квадрат второго выражения, выполнить вычисления.) - Сформулируйте правило.
4) Закрепление .
а)-Комментированное письмо. Учитель пишет на доске.
(р -5)(р+5)= (х -3)(х+3)=
б)-Устно: Умножьте многочлены:
г) Игра “Счастливый билетик”.

Ученики по очереди вытаскивают билетик и решают пример устно.
(у -6)( у +6) (х+2) (х-2) (а+9) (а-9)
(1-с)(1+с) (0,5-х) (0,5+х) (m+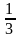 ) (m-
) (m- 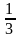 )
)
(0,9x+m) (0,9x-m) (x -1)(x+1) (3+m) (3-m)
-Почему формула называется формулой сокращенного умножения
–На доске заготовлен алгоритм определения вида зависимости, который учитель построчно открывает после того, как учащиеся проговаривают соответствующий пункт.
Алгоритм работы по формуле (а-в)(а+в)=а2-в2.
Записать квадрат первого выражения.
Поставить минус.
Записать квадрат второго выражения.
Выполнить возведение одночленов в квадрат.
Первичное закрепление темы.
Организация учебного процесса на этапе :
№854 (г,з,и) (на доске). Фронтально, 1 учащийся комментирует и записывает решение.
г) (х+3)(х-3)=х2-32=х2-9;
з) (2а-3в)(3в+2а)=(2а)2-(3в)2=4а2-9в2;
и) (8с+9d)(9d-8c)=(9d)2-(8c)2=81d2-64c2.
№857(в,д,ж) (на доске). Фронтально, 1 учащийся комментирует и записывает решение.
в) (9а-в2)(в2-9а)=(9а)2-(в2)2=81а2-в4;
д) (10р2-0,3q2)(10р2+0,3q2)=(10р2)2-(0,3q2)2=100p4-0,09q4);
ж) (c4+d2)(c4-d2)=(c4)2-(d2)2=c8-d4.
Вычислите , не производя вычисления «встолбик», используя формулу.
199∙201= (200-10)(200+1)= 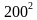 -
- 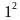 =3999
=3999
48∙52=(50-2)(50+2)=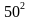 -
- 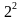 = 2500-4=2496
= 2500-4=2496
5)Обучающая самостоятельная работа
1.Выполнить умножение: Вариант 1
1 (3x+4)(3x+4)=
2.(2-5n)(2+5n)=
3.(9p+4a)(9p-4a)=
4.(7c2+4x)(7c2+4x)=
5.(5-6b2)(5+6b2)=
6.(0,8a3-1)(0,8a3+1)
1.Выполнить умножение: Вариант 2.
1.(2a+3)(2a+3)=
1.(2a+3)(2a+3)=
2.(5-4m)(5+4m)=
3.(8b+6c)(8b-6c)=
4.(5x+3a2)(3a2-5x)=
5.(4-7d2)(4+7d2)=
6.(1+0,9a4)(1-0,9a4)=
6)Проверка , ответы на доске. Обмениваются с соседом и ставят оценку друг другу. По желанию выставляются в журнал.
-Кто получил «5», «4», «3» поднимите руку?
7)Рефлексия. Как бы вы назвали тему урока?
-Запишем в тетради. «Умножение разности двух выражений на их сумму»
-Как умножить разность двух выражений на их сумму?
8)Задание на дом: правило,№913,915 и любой номер из следующих на выбор.

Комплекс упражнений для глаз:
1) вертикальные движения глаз вверх-вниз;
2) горизонтальные вправо-влево;
3) вращение глазами по часовой стрелке и против;
4) закрыть глаза и представить по очереди цвета радуги (Каждый охотник желает знать, где сидит фазан»).







 )(∆ +
)(∆ + 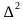 -
- 

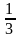 ) (m-
) (m- 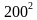 -
- 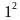 =3999
=3999 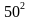 -
- 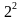 = 2500-4=2496
= 2500-4=2496










