Тема 1: Уравнение прямой в пространстве.
З адание: записать конспект и выполнить самостоятельную работу.
адание: записать конспект и выполнить самостоятельную работу.
Пример 1. Составить уравнение прямой, проходящей через две точки:
М1(3; 5; 2) и М2(4; 8; 1).
М1(х1;у1;z1) М2(х2;у2;z2)
Решение.
Подставив в уравнение прямой соответствующие координаты, получим:
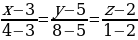
Упростим: 
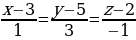
Ответ: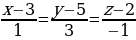
Пример 2. Составить уравнение прямой, проходящей через две точки:
М1(3; 4; -2) и М2(5; 2; -1).
М1(х1;у1;z1) М2(х2;у2;z2)
Решение.
Подставив в уравнение прямой соответствующие координаты, получим:
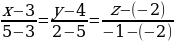
Упростим: 
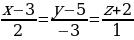
Ответ: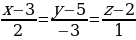 Самостоятельная работа
Самостоятельная работа
Пример 1. Составить уравнение прямой, проходящей через две точки:
М1(2; 4; 8) и М2(1; 5; 7).
Пример 2. Составить уравнение прямой, проходящей через две точки:
М1(7; 3; 4) и М2(2; 6; 9).
Пример 3. Составить уравнение прямой, проходящей через две точки:
М1(4; -2; 4) и М2(5; -6; 3).
Тема 2: Уравнение плоскости в пространстве
Задание: записать конспект и выполнить самостоятельную работу
П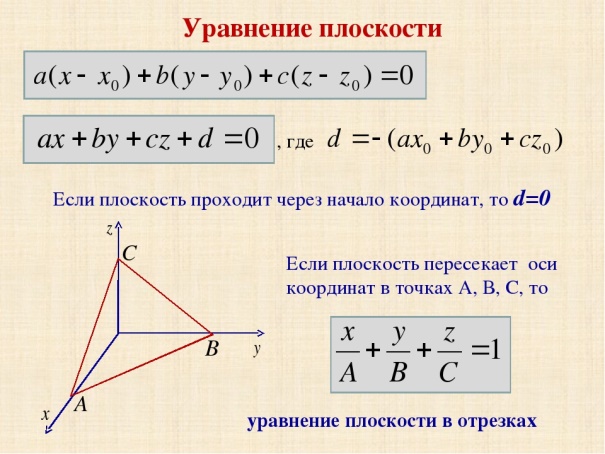 ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.
2х+3у-z+3=0
2·(-1)+3·2-7+3=-2+6-7+3=0 – верно.
Ответ: точка В (-1; 2; 7) принадлежит плоскости.
Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0
Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0
0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно
Ответ: точка Е(0; 4; -6) не принадлежит плоскости.
Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0
Решение: Подставим координаты точки в уравнение и найдем D.
-3·1+2·5-(-2)+D=0,
-3+10+2+ D=0,
9+ D=0,
D=-9.
Ответ: D=-9.
Самостоятельная работа
Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением
3х+2у-4z+1=0
Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением
х-3у-5z+6=0
Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0
Тема 3: Уравнение сферы.
Задание:
-
Записать конспект
-
Решить задания №1, №2
Конспект:
О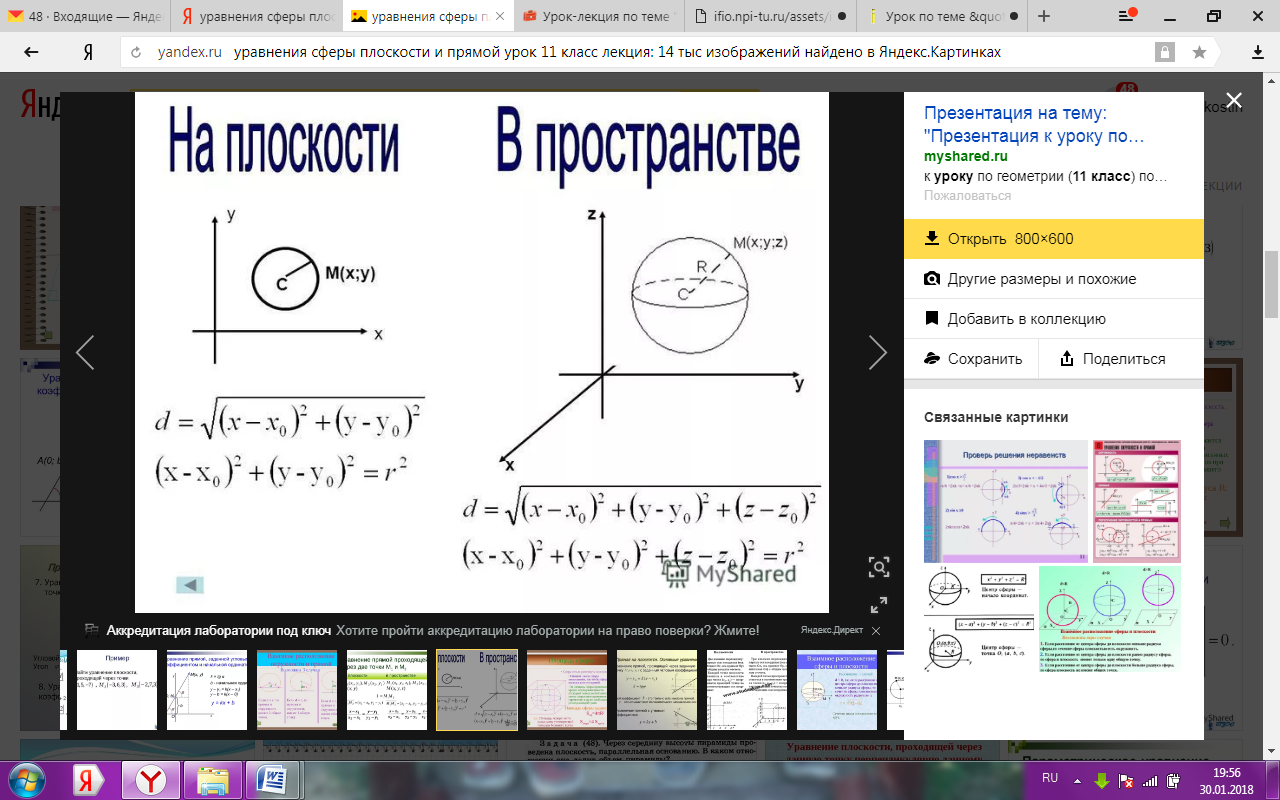 пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
R – радиус сферы, т. О – центр сферы.
(х-х0)2+(у-у0)2+(z-z0)2=R2 , где
точка О(x0, y0, z0) – центр сферы.
Пример 1.
Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.
Решение:
О(x0, y0, z0)
О((1; 2; -5). Значит x0=1, y0=2, z0=-5, R=3.
Подставим в уравнение сферы: (х-1)2+(у-2)2+(z-(-5))2=32.
Упростим: (х-1)2+(у-2)2+(z+5)2=9.
Ответ: (х-1)2+(у-2)2+(z+5)2=9.
Пример 2. Дано уравнение сферы: (х-6)2+(у+3)2+(z-4)2=64. Найти координаты центра и радиус сферы.
Решение:
1)найдем координаты центра: (х-6)2+(у-(-3))2+(z-4)2=64
x0=6, y0=-3, z0=4
2)найдем радиус: R2=64, R=√64=8,
Ответ: О(6, -3, 4), R = 8.
Решить задания:
Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6
Задание 2. Дано уравнение сферы (х-3)2+(у+7)2+(z-8)2=25. Найти координаты центра и радиус сферы.





 адание: записать конспект и выполнить самостоятельную работу.
адание: записать конспект и выполнить самостоятельную работу.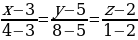

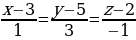
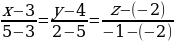
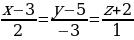
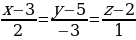 Самостоятельная работа
Самостоятельная работа ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0 пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.


















