Урок № 3 Ознаки подільності на 9 і 3

Урок № 3

Ознаки подільності на 9 і 3

Мета уроку: доповнити знання учнів ознаками подільності на 9 і на 3, навчити користуватися цими ознаками під час розв’язування вправ; формувати математичні комунікативні та загально­освітні компетентності, культуру усних обчислень; розвивати вміння зосередитися на головному.

Очікувані результати: учні повинні вміти наводити приклади чисел, які діляться націло на 9 і на 3, формулювати ознаки подільності на 2, 3, 5, 9 і 10 та розв’язувати вправи, що передбачають використання ознак подільності на 2, 3, 5, 9, 10.

Обладнання та наочність: підручник, презентація, відеоматеріал.

Тип уроку: урок засвоєння нових знань.

Словничок (глосарій):

• Кратне натуральному числу – число, яке ділиться націло на дане натуральне число.

• Ознака подільності на натуральне число – необхідна і достатня умова подільності націло деякого натурального числа на дане натуральне число.

■ I. Перевірка додаткового завдання

Розв’язання

Кількість олівців має бути числом, кратним числу 5. Тобто може бути 90 олівців і 75 олівців.

■ II. Актуалізація опорних знань

▪Опитування

1. Які числа називають парними?

2. Запишіть найменше трицифрове непарне число.

3. Допишіть до числа 127 праворуч таку цифру, щоб одержане число ділилося і на 2, і на 5.

4. Встановіть без обчислень, чи ділиться на 5 сума .

5. Чи ділиться на 10 добуток чисел 3733 і 45?

6. Запишіть найбільше чотирицифрове число, яке ділиться на 5 і сума цифр якого дорівнює 11.

Відповіді до запитань

1. Числа, що діляться на 2. 2. 101. 3. 1270. 4. Ні. 5. Ні. 6. 9200.

■ III. Формулювання завдань заняття; мотивація навчальної діяльності

На минулому занятті ми переконалися, що за записом можна дізнатися, чи ділиться воно на 2, на 5 або 10. Перевірте, чи можна скористатися аналогічною ознакою, щоб встановити, чи ділиться на 3 число, запис якого закінчується цифрою 3?(ознаки аналогічні ознакам подільності на 2, на 5 і на 10, у даному випадку не «працюють»). На цьому занятті ви дізнаєтесь як, не виконуючи ділення, дізнатися, чи ділиться число на 3 і на 9. Погодьтеся, це зручно.

■ IV. Засвоєння нових знань

План викладання нового матеріалу

1. Ознаки подільності на 9.

2. Ознаки подільності на 3.

Теоретичний матеріал

▪ Запитання для опрацювання

1. Визначте, чи є правильним твердження:

а) якщо число ділиться на 9, то воно ділиться й на 3;

б) якщо число ділиться на 3, то воно ділиться й на 9.

1. Ознака подільності на 9

На 9 діляться всі ті натуральні числа, сума цифр яких ділиться на 9. Якщо сума цифр числа не ділиться на 9, то це число не ділиться на 9.

Приклади

• Сума цифр числа 45981 дорівнює 4 + 5 + 9 + 8 + 1 = 27 – ділиться на 9, отже, й число 45981 ділиться на 9.

• Сума цифр числа 32 758 дорівнює 3+2+7+5+8=25 – не ділиться на 9, отже, й число 32 758 не ділиться на 9.

2. Ознака подільності на 3

На 3 діляться всі ті натуральні числа, сума цифр яких ділиться на 3. Якщо сума цифр числа не ділиться на 3, то це число не ділиться на 3.

Приклади

• Сума цифр числа 51 342 дорівнює 5 + 1 + 3 + 4 + 2 = 15 – ділиться

на 3, отже, й число 51 342 ділиться на 3.

• Сума цифр числа 29 126 дорівнює 2 + 9 + 1 + 2 + 6 = 20 – не ділиться на 3, отже, й число 29 126 не ділиться на 3.

■ V. Первинне закріплення знань

▪ Виконання усних вправ

1. Які з чисел 513, 45 081, 290 036 діляться на 3; на 9?

2. Знайдіть чотирицифрове число, яке:

1. ділиться на 3;

2. ділиться на 9;

3. ділиться на 3, але не ділиться на 9.

Варіант № 1

1. Поставте замість зірочки таку цифру, щоб отримане число ділилося на 9:

а) 235*; б) 47*2; в) *711.

2. Дано числа:

а) 35*; б) 1*2; в) *71.

Відновіть цифри, якщо відомо, що вони діляться на 3. Зазначте всі можливі варіанти.

Варіант № 2

1. Запишіть п’ять двоцифрових чисел, які діляться і на 2, і на 3. На яке ще число діляться всі ці числа?

2. Дано цифри 3, 4, 5 і 6. Складіть із них усі трицифрові числа, що діляться і

на 3, і на 5.

Розв’язання до варіантів

Варіант № 1

1. а) — ділиться на 9;

б) — ділиться на 9;

в) — ділиться на 9.

Відповідь: а) 8; б) 5; в) 9.

2. а) 35*: ; ; —

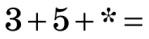
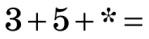
діляться на 3;

б) 1*2: ; ; ; — діляться на 3;

в) *71: ; ; — діляться на 3.

Відповідь: а) 1; 4; 7; б) 0; 3; 6; 9; в) 1; 4; 7.

Варіант № 2

1. Щоб число ділилося і на 2, і на 3, його запис має закінчуватися парною цифрою, а сума його цифр — ділитися на 3. Це можуть бути, наприклад, числа 30; 60; 90; 18. Всі вони діляться на 6.

Відповідь: 30; 60; 90; 12; 18.

2. Запис чисел 345; 435 — закінчується цифрою 5, сума цифр становить 12.

Запис чисел 555, 645, 465 закінчується цифрою 5, сума цифр становить 15.

Відповідь: 345; 435; 555; 645; 465.

■ VI. Підбиття підсумків заняття

▪ Запитання

1. Як швидко дізнатися, чи ділиться на 2 сума:

а) ;

б) ;

в) ?

2. Як швидко дізнатися, чи ділиться на 2 різниця:

а) ;

б) ;

в) ?

3. Чи є правильним твердження, що число 25 410 ділиться:

а) на 2; б) 9; в) 10; г) 5; д) 45?

■ VІIІ. Додаткове завдання

1. Знайдіть трицифрове число, запис якого починається з цифри 2 і яке ділиться на 2, 5