Урок алгебры 7 класс И.Г. Дорофеев Корни уравнения

Этапы урока

Содержание учебного материала.

Деятельность

учителя

Деятельность

обучающихся

Формирование УУД

1

Организационный.

Приветствие, проверка готовности учащихся к уроку. Проверка выполнения домашнего задания. Сегодня закрепим умение решать линейные уравнения, обобщим их и узнаем немало интересного.

Задают вопросы по д/з ( если они возникали при решении).

Отвечают на вопрос учителя.

Личностные: самоопределение, смыслообразование.

Регулятивные: целеполагание, планирование, саморегуляция.

Коммуникативные: планирование сотрудничества с учителем и сверстниками.

2

Актуализация знаний

Завершить фразы:

1. Уравнение – это равенство …;

2. Корень уравнения – число, …;

3. Решить уравнение – значит …;

4. Линейное уравнение с одним неизвестным – уравнение вида …;

5. Любой член уравнения можно …;

6. Обе части уравнения можно … .

Математическая разминка

1. Из данных выражений выбрать уравнения и объяснить свой выбор: а) 2a + 3b – c ; б) 8 – 3 = 5:1;
   в) 2х = 10; г) 8( x – 3) = 4x + 90;

д) 3y +2(y – 7);

е) 2х = 3 – y .

Решите уравнения:

а) 6х = - 2; б) – 5х = 1;
в) 0х = 4; г) 4х = 0;

д) 0х = 0.

Для сильных(самост-но с послед. проверкой) :

Составить уравнение с одной переменной по данным таблицы и решить их (устно)

1. Равенство, содержащее неизвестное число, обозначенное буквой.

2. Число, которое при подстановке его в уравнение вместо неизвестного обращает его в верное числовое равенство.

3. … найти его корни или установить, что их нет.

4. ax = b

5. … перенести из одной части уравнения в другую с противоположным знаком.

6. … разделить или умножить на одно и тоже отличное от нуля число.

По ходу решения уч-ся комментируют используемые ими приемы и формулируют правила.

1. 3x – 1 = x + 1,

3x – x = 1 + 1,

2x = 2,

x = 1;

1. 4y + 5 = 2y + 2,

4y - 2y = 2 – 5,

2y = -3,

y = -1,5;

1. 7z – 9 = z + 4,

6z = 13,

z = 13/6;

1. 3a + 1 = 3a – 1,

0a = -2,

0 = -2,

решений нет;

1. b – 9 = b – 9,

0 = 0,

бесконечное множество решений;

1. ½ c – 0,1 = c + 7/3,

-1/2 c = 70/30 + 3/30,

-1/2 c = 73/30,

c = -146/30.

Р: прогнозирование, контроль, коррекция, оценка.

П: логические.

К: постановка вопросов, разрешение конфликтов.

3

Устный счет

Экскурс в мифологию Древней Греции.

Расшифруйте слово, которое здесь загадано. Для этого нужно правильно записать ответы устных примеров.

Знаете ли вы, откуда произошло крылатое выражение «Путеводная нить»? С каким мифом Древней Греции оно связано?

(миф о Тесее и Минотавре)

Получили слово «ЛЕГЕНДА»

Сообщение учащегося по данному вопросу, остальные учащиеся слушают.

Это легенда о Тесее, который, пройдя через лабиринт, помог спастись юношам и девушкам, отданным на съедение человеку-быку Минатавру. Вернуться обратно из лабиринта помогла дочь царя Миноса Ариадна. Перед входом в лабиринт она дала ему клубок ниток. И Тесей привязал у входа конец клубка, а затем, идя по лабиринту, постепенно его разматывал. Потом он по этой нитке смог вернуться обратно.

Л: самоопределение, нравственно-этическая ориентация.

П: синтез объектов и явлений по данной теме.

4

Применение изученного

Вам тоже предстоит пройти через лабиринт. Желаю всем удачного выхода из лабиринта!

1. Выполнить задание №1

1. Выполнить задание №2

1. Выполнитьзадание№3 Дидактический материал стр.123

2. Выполнить задание №4 Дидактич.м.стр38

3. 

(все задания выполнены верно – учащиеся выходят на слайд «Ваша оценка – 5»; допущены 1 – 2 ошибки – «Ваша оценка – 4»; более двух ошибок – учащиеся не могут выйти из лабиринта – за работу на уроке получают «3»)

Учащиеся выбирают правильный ответ, обосновывая свой выбор.

Самостоятельная работа .

Л: самоопределение.

Р: контроль )сравнение способа действия с его результатом), коррекция, саморегуляция.

П: логические (анализ объектов с целью выделения признаков).

К: выявление проблемы; поиск и оценка способов ее решения.

4

Применение изученного

(для тех, кто справился раньше остальных)

Дополнительные за№ 352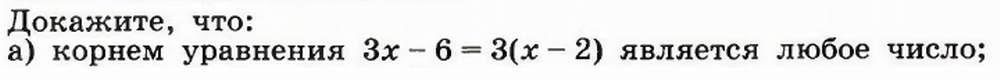

№353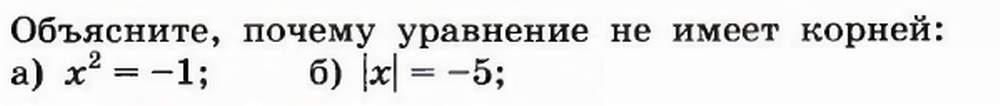

Самостоятельно решают.

физкультминутка

5

Информация о домашнем задании

№ 349, 350(в, г), 351(в, г), 352(б)

Записывают д/з в дневники.

6

Подведение итогов урока

Имеют ли корни данные уравнения? Сколько? Поясните свой ответ.

1. 4a – 12 = 4a + 7

2. 5b – 1 = 4b + 4

3. 4c – 3 – 4c = -3

1. 4a – 4a = 19,

0a = 19,

0 = 19; корней нет, т. к. уравнение не обращается в верное равенство ни при каком значении переменной.

1. 5b – 4b = 4 + 1,

b = 5; один корень.

1. 4c - 3 – 4c = -3,

-3 = -3; бесконечное множество решений, т. к. равенство верно при любых значениях переменной.

Р: оценка – осознание уровня и качества усвоения; контроль.

7

Рефлексия

Итак: мы с вами сегодня закрепили умение решать линейные уравнения с одной переменной.

Продолжите, пожалуйста фразы:

«Сегодня на уроке я повторил …».

«Сегодня на уроке я узнал …».

«Сегодня на уроке я научился …»

Всем спасибо за урок.

Кто-то вслух, кто-то мысленно это делает.

К: умение с достаточной полнотой и точностью выражать свои мысли.