Урок алгебры в 10классе по теме "Тригонометрические функции числового аргумента"

Тригонометрические функции числового аргумента

Учитель математики Выборных Т.И.

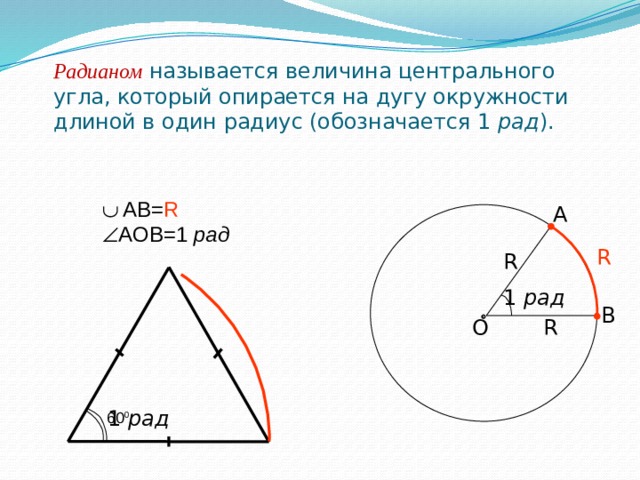
Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1 рад ).

 AB= R

 AOB=1 рад

A



R

R

1 рад





B

R

O

1 рад

60 0

Радианная мера уг ла.

Формула . Связь радианной и градусной мер:

Задание 1. Выразить величины углов в радианной мере:

Задание 2. Выразить в градусной мере величины углов:

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

ЧИСЛОВАЯ ОКРУЖНОСТЬ

Определение. Числовая окружность – единичная окружность с установленным соответствием (между действительными числами и точками окружности).

Уравнение числовой окружности : x 2 + y 2 = 1

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

ЧИСЛОВАЯ ОКРУЖНОСТЬ

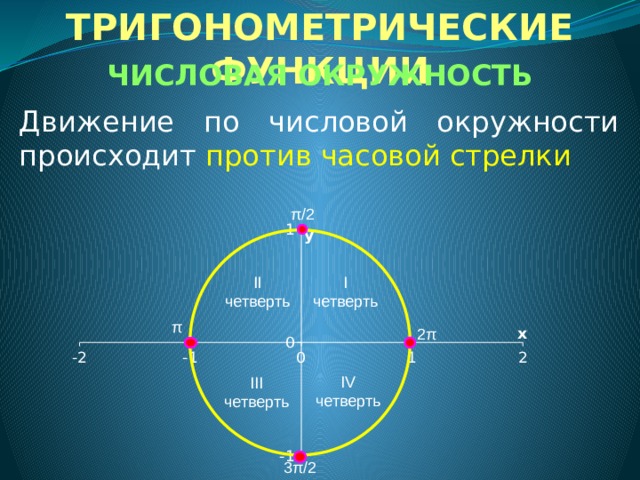
Движение по числовой окружности происходит против часовой стрелки

π/2

II четверть

I четверть

π

2π

IV четверть

III четверть

3π/2

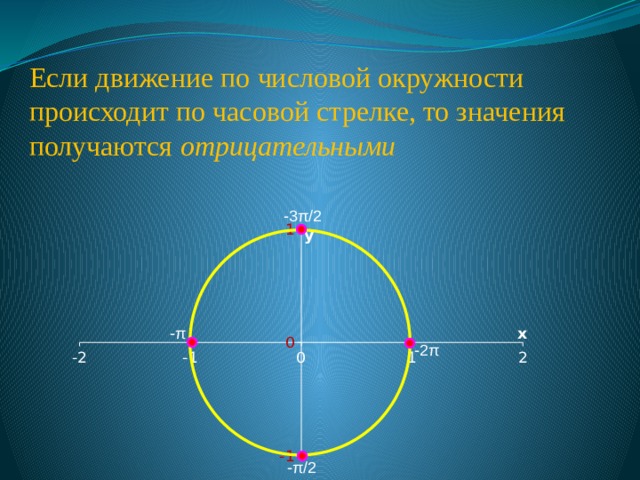
Если движение по числовой окружности происходит по часовой стрелке, то значения получаются отрицательными

-3π/2

-π

-2π

-π/2

• Определение. Тригонометрические функции - это функции, устанавливающие зависимость между сторонами и углами треугольника. Тригонометрические функции угла α определяются при помощи числовой окружности, а также из прямоугольного треугольника (для острых углов).

Определение. Если точка М числовой окружности соответствует числу t , то абсциссу точки М называют косинусом числа t и обозначают cos t , а ординату точки М называют синусом числа t и обозначают sin t .  

M (t)

sin t

cos t

Если M(t) = M(x; y), то

x = cos t,

y = sin t.

В оглавление

Определение. Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают tg t.

Определение. Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают ctg t.

Определение тригонометрических функций

Отрезок на оси x от -1 до 1 называется линией косинусов.

Отрезок на оси y от -1 до 1 называется линией синусов.

Отсюда следуют свойства синуса и косинуса: |sint| ≤ 1, |cost| ≤ 1.

Линия тангенсов параллельна оси y и проходит через точку (1; 0) .

Линия котангенсов параллельна оси x и проходит через точку (0; 1) .

Для любого допустимого значения t справедливы равенства:

• sin ( t + 2πk) = sin t ,
• cos ( t + 2πk) = cos t .
• tg ( t + πk) = tg t ;
• ctg ( t + πk) = ctg t , где k є Z.

Определение

Тригонометрические функции числового аргумента t – функции y = sin t, y = cos t, y = tg t, y = ctg t .

Основные соотношения, связывающие значения различных тригонометрических функций : . уравнение единичной окружности -

- основное тригонометрическое тождество.

tgt∙ctgt=1 - связь между тангенсом и котангенсом