Урок геометрії в 7 класі за темою: Ознаки рівності трикутників

Урок геометрії в 7-А класі

Тема: Перша і друга ознаки рівності трикутників.

 Мета: закріпити знання учнів про зміст та способи засто­сування теорем, що виражають першу і другу ознаки рівності трикутників, для розв'язування задач на дове­дення рівності трикутників; виробити вміння добирати аргументацію і доводити рівність трикутників із вико­ристанням першої і другої ознак рівності трикутників, а також використовувати доведення рівності трикутників для доведення рівності відрізків, кутів і для доведення паралельності прямих.

Хід уроку

І. Організаційний етап 

ІІ.Перевірка домашнього завдання 

1. Для перевірки засвоєння учнями змісту теорем, що виражають першу і другу ознаки рівності трикутників, проводимо математичний диктант.

Математичний диктант.

Варіант 1 [2]
1.У трикутниках KNO і PQT [ABC і DEF] рівні сторониKN [АВ] і PQ [DE] і кути К [А] і Р [D]. Яка ще умо­ва має виконуватися, щоб ці трикутники були рівні за першою ознакою?

2.У трикутниках  ABC  і  DEF  [ MPQ  і  KLT ]  сторони   і ВС  [ MP  і  PQ ]  дорівнюють відповідно сторонам  DE  і EF  [ KL  і LT ]. Трикутники ці не рівні. Що можна сказати про кути В і Е  [Р і L]?

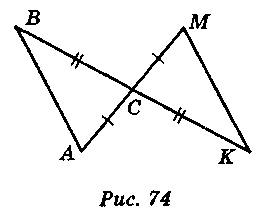
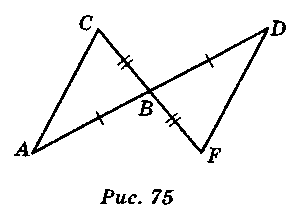
3.Доведіть рівність трикутників ABC і МКС (мал. 74) [ABC і DBF (мал. 75)].

 
ІІІ.Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів 

ІV.Актуалізація опорних знань і вмінь учнів

Усні вправи
1.Відомо, що пари трикутників на рис. 78 рівні. Запишіть відповідні рівності.

  

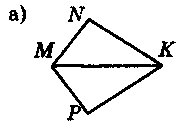
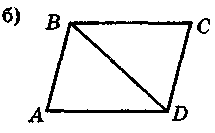
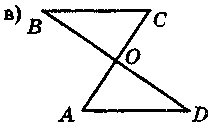
Рис. 78
2.Які елементи трикутників MNK і DEF мають бути рів­ними, щоб виконувалася рівність трикутників за першою ознакою?

V.Розв'язування задач і вправ. 

Учні працюють, об'єднавшись у чотири групи (по 4—5 учнів). Учням треба показати вміння використовувати знання першої і другої ознак рівності трикутників під час розв'язування задач. Обговорення питань, що виникатимуть, відбуватиметься шляхом колективного обдумування — «мозкового штурму», який проводиться так:
Один бажаючий з класу записує умову задачі на дошці, щоб під час обдумування та пошуку розв'язання її бачили учні.

Усі учасники «штурму» мають право висувати свої ідеї щодо розв'язування завдання.
Коли учасники групи з'ясовують, що ідей (пропозицій) достатньо, їх висування припиняється. 
Подані ідеї аналізуються (обговорюються) у групах.
Після обговорення група зупиняється на одному - зі способів розв'язування — раціональнішому з їх точки зору.
Якщо окремий учень групи не погоджується, що обраний спосіб найдоцільніший, то він може розв'язати задачу своїм способом. 

 Задача 1. Відомо, що трикутники ABC і НТО рівні. На сторонах АВ і НТ відкладено рівні відрізки АК і НМвідповідно. Доведіть рівність трикутників АСК та НОМ.
Вказівка щодо організації роботи. Учні, працюючи у групах, висувають пропозиції щодо розв'язування задачі (чим більше пропозицій - тим краще). Вони вільно виражають свої думки, колективно обговорюють їх. У процесі колективного обговорення знаходять раціональний спосіб розв'язування. Якщо деякі запропоновані способи хибні, то їх треба відкинути і вказати, в чому полягає їх помилковість. 

Задача 2. У трикутнику ABC 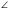A = 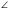C. На сторонах АВ іАС від­кладено рівні відрізки AM і СК відповідно. Знайдіть довжину відрізка АК, якщо CM = = 14 см. 
Вказівка щодо організації роботи. Висуваються всі можливі ідеї розв'язування задачі. Обговорення проходить у групах: кожна група вибирає свій спосіб розв'язування. Біля дошки після виконання завдань працюють одночасно по одному учневі від кожної групи. Кожна група захищає свій спосіб розв'язування, учні обирають найраціональніший. 

Задача 3. У трикутнику ABC AB = BC. Бісектриса кута В перетинає сторону АС у точці К. Знайдіть кут між прямими АС і ВК. 
Вказівка щодо організації роботи. Завдання кожен учень виконує самостійно, спосіб розв'язування не оголошується, наприкінці перевіряється відповідь.

VІ.Підсумок уроку.

Запитання до класу:

1Якими ознаками рівності ви користувались під час розв’язування задач?

2.Чи все вам вдалося під час розв’язування задач?

VІІ.Домашнє завдання: §12. Повторити ознаки рівності трикутників. Розв’язати: № 262, 264.