Урок информатики в 9 классе по теме: «Алгоритм Евклида»

Урок информатики в 9 классе по теме: «Алгоритм Евклида»

Цели урока:

• Образовательные:

• научиться применять алгоритм Евклида для нахождения НОД двух и трех чисел;

• закрепить навыки по использованию алгоритмических структур «ветвление» и «цикл с предусловием»;

• получить опыт написания и отладки программ на языке программирования Паскаль.

• Воспитательная:

• воспитание самостоятельности и ответственности при изучении нового материала.

• Развивающая:

• развитие внимания и аналитического мышления.

Тип урока: комбинированный.

Технические средства: компьютеры, проектор, экран для проектора.

Программное обеспечение: операционная система Windows, редактор презентаций Microsoft PowerPoint, система программирования Turbo Pascal.

План урока:

I. Организационный момент.

Здравствуйте, ребята. Тема нашего сегодняшнего урока: «Алгоритм Евклида». Конечно, имя этого математика вам хорошо известно. Он внес важный вклад в развитие науки математики. А сегодня на уроке вы узнаете, как одно из сформулированных им правил используется в информатике.

II. Актуализация знаний.

Последние несколько уроков были посвящены основам программирования на языке Паскаль. Ответьте на вопросы:

• Какие типы алгоритмических структур вы знаете?

• Какая структура называется линейной?

• Какая структура называется разветвляющейся?

• Какая структура называется циклической?

III. Изучение нового материала.

Задача, которую мы с вами будем решать, известна вам из курса математики 6 класса. Нам нужно найти наибольший общий делитель (НОД) двух чисел М и N.

Что такое НОД двух натуральных чисел? (Это самое большое натуральное число, на которое они делятся нацело). (Слайд 2)

Давайте вспомним, как вы находили НОД на уроках математики в 6 классе? (Слайд 3)

Если этот алгоритм переводить на язык программирования, то придется решить следующие задачи (Слайд 4):

1. Разложить числа на простые множители.

2. Найти общие множители.

3. Найти их произведение.

Каждая из этих задач по-своему сложная. Поэтому для составления программы мы будем использовать алгоритм, который был сформулирован в 3 веке до н.э. древнегреческим математиком Евклидом. Идея этого алгоритма основана на двух свойствах (Слайд 5):

1. Если MN, то НОД (M, N) = НОД (M-N, N)

2. НОД (M, M) = M

Например: НОД (12, 18) = НОД (12, 18-12) = НОД (12, 6) = НОД (12-6, 6) = НОД (6, 6) = 6.

Иными словами, алгоритм Евклида для «ручного» счета выглядит так (Слайд 6):

1. Если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма.

2. Заменить большее число разностью большего и меньшего из чисел.

3. Вернуться к выполнению п. 1.

Рассмотрим блок-схему для описания алгоритма Евклида (Слайд 7):

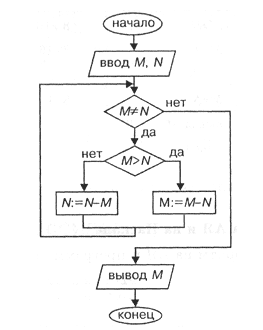
Какие алгоритмические структуры в ней присутствуют? (Цикл-пока с вложенным ветвлением). Как они работают? (Слайды 8-9)

Рассмотрим подробно трассировочную таблицу алгоритма для исходных значений M=32, N=24 (Слайды 10-34).

Теперь вернемся к блок-схеме алгоритма Евклида и попробуем написать на ее основе программу на языке Паскаль (Слайды 35-36)

Program Evklid;

var m, n: integer;

begin

writeln (’Введите m и n ’);

readln (m, n);

while mn do

begin

if mn

then m:=m-n

else n:=n-m

end;

write (’НОД=’, m)

end.

IV. Практическая работа.

1. Выполнить на компьютере полученную программу. Протестировать ее на значениях:
1) M=32, N=24; 2) M=696, N=234.

2. Составить программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
M х N = НОД (M, N) х НОК (M, N).

V. Домашнее задание.

Составить программу нахождения наибольшего общего делителя трех чисел, используя формулу:

НОД (A, B, C) = НОД (НОД (A, B), C).

VI. Подведение итогов, выставление оценок.