Урок математики. Тема:"Длина окружности"

ГКОУ школа-интернат

г.Хотьково Московской обл.

Учитель математики:

Меленчук Е.И.

Цели урока

• Повторить основные понятия темы «Окружность».
• Вывести формулу для вычисления длины окружности.
• Учиться применять эту формулу при решении задач.

План урока

• Проверка домашнего задания
• Определение темы и целей урока
• Актуализация опорных знаний учащихся
• Изучение нового материала
• Практическая работа.
• Коррекционная работа(АБВГДейка)
• Закрепление изученного материала (решение задач)
• Самостоятельная работа (тест)
• Физкультминутка
• Исторический материал( презентация числа пи)
• Итоги урока
• Домашнее задание

Актуализация знаний

• 1 . Вспомнить определение окружности и назвать её основные элементы ( радиус; диаметр; центр)

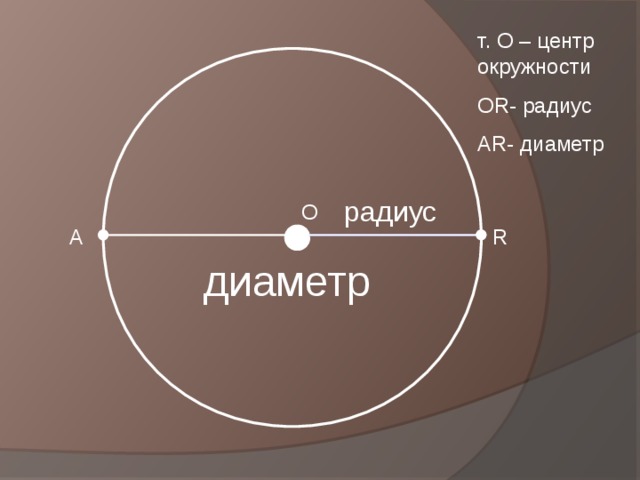
т. О – центр окружности

ОR- радиус

АR- диаметр

радиус

О

R

А

диаметр

r - радиус

d – диаметр

d=2*r

R=d:2

С

В

D

O

А

E

L

F

Перечислите все радиусы и диаметры

K

Актуализация знаний

• 2. Округлить число 3,1415926

до тысячных

до сотых

до десятых

Длина окружности

Математика 6 класс. Н.Я.Виленкин.

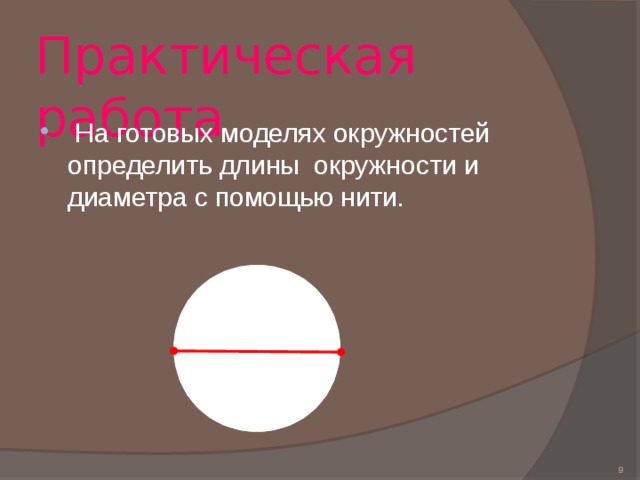
Практическая работа

• На готовых моделях окружностей определить длины окружности и диаметра с помощью нити.

Диаметр

Великий древнегреческий математик Архимед (III в. до н.э.), выполнив множество измерений, установил, что длина окружности

примерно в раза

больше её диаметра.

Можно сделать клик на кнопку «Показать» несколько раз.

22

Число называют Архимедово число.

7

Это число обозначают греческой буквой

(читается «пи»).

Обозначим длину окружности буквой С,

а длину диаметра буквой d,

то С : d = . Поэтому С = d.

Так как диаметр окружности вдвое больше ее радиуса

d = 2r, то

C = 2 П r

11

Формулы длины окружности читаются так:

• C=πd – «цэ» равно «пи дэ»
• C=2πr – «цэ» равно двум «пи эр»

Выражение π ≈ 3,14 читают:

«Пи приближенно равно трем целым четырнадцати сотым»

11

АБВГДейка

• 1 . час…ное
• 2. пр…порц…я
• 3. …кружность
• 4. д…аметр
• 5. площ…дь

• 6. отн…шение
• 7. рад…ус
• 8. ма…таб
• 9. дл…на
• 11. ч…сло

Физкультминутка. Можно использовать интерактивную доску.

12 см

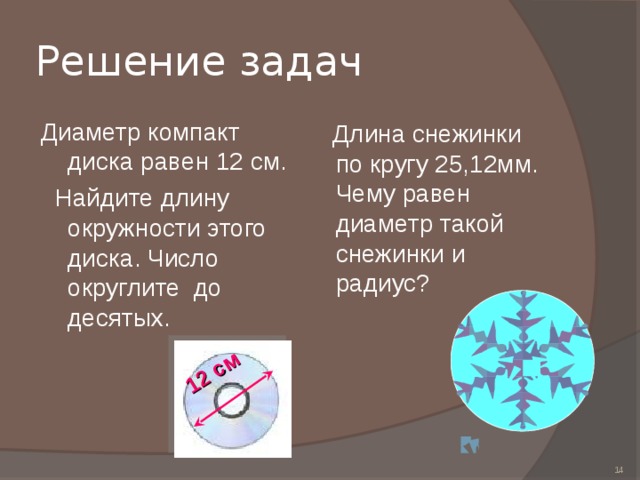
Решение задач

Диаметр компакт диска равен 12 см.

Найдите длину окружности этого диска. Число округлите до десятых.

Длина снежинки по кругу 25,12мм. Чему равен диаметр такой снежинки и радиус?

Задача

Радиус земного шара приближенно равен 6,35тыс. км. Скольким тысячам километров равен диаметр и длина экватора Земли? (Число тысяч округлите до десятых)

Математика 6 класс. Н.Я.Виленкин. № 874

                                                              ТЕСТ

1.Отрезок, соединяющий две точки окружности и проходящий через центр.

А) радиус;   Б) сторона;   В)луч;     Г) диаметр.

2.Число π равно

А) 1,34;           Б) 3,14;           В) 3,91;        Г) 4,13.

3.Формула длины окружности

А) С=πd     Б) C=2πd       В) С=πr          Г) C=2r

4.Чему равен радиус окружности, диаметр  которой 7,6 см?

      А) 4,46      Б) 15,2          В) 3,8          Г) 3,14

5.Чему равен диаметр окружности, радиус которой равен 2,7?

  А) 1,35      Б) 3,14 В) 5,4 Г) 7,29

Правильные ответы на тест

• 1. Г) диаметр.
• 2. Б) 3,14;
• 3. А) С=πd  
• 4. В)   3,8
• 5. В) 5,4

• Обозначение этого числа произошло от греческого слова , обозначающего «периферия» — то есть окружность.
• Несмотря на то, что числом  пользовались еще со времен древних греков и египтян, название это число получило только в 1706 году.  Впервые его использовал математик из Англии – Уильям Джонс. Однако, мир признал  под этим названием только в 1736 году, когда его систематически стал употреблять Леонард Эйлер.

Специалисты считают, что 

история числа Пи  началась еще в древнем Вавилоне. Более того, именно число Пи стало причиной краха Вавилонской башни. Якобы вавилонские маги пользовались этим числом при постройке башни, однако вавилоняне пользовались лишь первой цифрой числа  - то есть тройкой. И именно из-за этого они так и не смогли построить вавилонскую башню.

День рождения числа Пи.

У числа Пи есть даже свой день – День рождения  числа Пи , празднуемый во всем мире. Неудивительно, что этот день – 14 марта – то есть 3,14 (третий месяц, 14 день). Этот праздник в 1987 году придумал  американский физик из Сан-Франциско Ларри Шоу.

На День Рождения числа Пи принято печь круглый пирог, с узором внутри пирога в виде значка .

6370км

320 км

Вычислите длину круговой орбиты искусственного спутника Земли, если спутник вращается на расстоянии 320 км от Земли, а радиус Земли равен 6370 км.

Л. С. Атанасян. Геометрия 7-9. №1108.

?

Показать

23

Итоги урока

• Закончи предложение
• Я узнал(а)…
• Я научился…..
• Самым интересным было….
• Эти знания мне пригодятся…

23

Домашнее задание

• П. 24 №867;869.
• С.139 вопросы Г(говори правильно)

СПАСИБО ЗА УРОК

Список литературы и ресурсы

• Математика 6 класс. Учебник для общеобразовательных учреждений. Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд М. :Мнемозина 2011.
• Дидактические материалы 6 класс. А.С.Чесноков, К.И.Нешков М.: Просвещение 2011 г.
• Интернет-ресурсы (число Пи)