Урок математики в 10 классе. "Отбор корней при решении тригонометрических уравнений"

МКОУ «Днепровская СШ»

Урок математики в 10 классе

«Отбор корней при решении тригонометрических уравнений, используя свойство периодичности тригонометрических функций»

(технология проблемного обучения).

Разработала Николаева Н.А.,

учитель математики

с. Днепровское 2016г.

Тема урока. «Отбор корней при решении тригонометрических уравнений,

используя свойство периодичности тригонометрических

функций».

Цель урока: познакомить учащихся с методом отбора корней при решении тригонометрических уравнений, используя свойство периодичности тригонометрических функций.

Задачи урока :

- обобщение знаний свойств тригонометрических функций с использованием

элементов исследования;

- применение данного метода при решении задач;

- развитие навыка самостоятельности в работе.

• содействовать воспитанию интереса к математике и ее приложениям, активности, мобильности, умения общаться, общей культуры.

Оборудование : интерактивная доска, презентация.

Ход урока.

1. Устная работа ( настрой на урок) – слайд № 1.

2. Самостоятельная работа « Проверь себя сам» - 1 уровень проблемного обучения (действие по образцу) - слайд №2.

3. Анализ результатов самостоятельной работы.

Задание № 7 вызвало затруднение. Задание, подобное домашнему заданию:

Решить уравнение 2sin2х + cosх + 4sinх + 1 = 0.

Указать корни, принадлежащие отрезку [5 π/2;7 π/2].

Повторное возникновение проблемной ситуации (подобное задание умышленно включено в домашнее задание без дополнительных разъяснений для того, чтобы учащихся подвести к проблемной ситуации и подтолкнуть к самостоятельному поиску решения).

1. Обсуждение подобных возникших вопросов при выполнении домашнего задания. Учитель умышленно анализирует возникшие вопросы после самостоятельной работы, чтобы дать возможность учащимся показать, как были решены подобные задания дома.

Решение домашнего уравнения – слайд № 3.

5.Постановка и раскрытие проблемы (анализ проблемной ситуации):

невозможность выполнить задание традиционными способами:

1. при решении уравнений имеем не табличные углы;

2. с данными промежутками сложно работать с помощью числовой окружности;

3. графический путь решения заданий не нравится ( сложен).

6. Актуализация прежних знаний – подготовка к разрешению проблемы - 2 уровень проблемного обучения (учитель вовлекает учащихся в совместный поиск путей решения проблемной ситуации и в процесс самого решения).

Вспоминаем :

а) Т(sin) = Т(cos)=2 πn, n N; т.е. при изменении величины угла на целое число оборотов значение синуса (косинуса) не меняется :

sin (x-2π) = sin (x+2 π)= sinx; cos(x-2 π)=сos(x+2 π)=cosx.

Пример: отобрать корни уравнения sinx=1/2 на отрезках [0; π];[2 π;3 π];

[-π;-2 π] c помощью числовой окружности

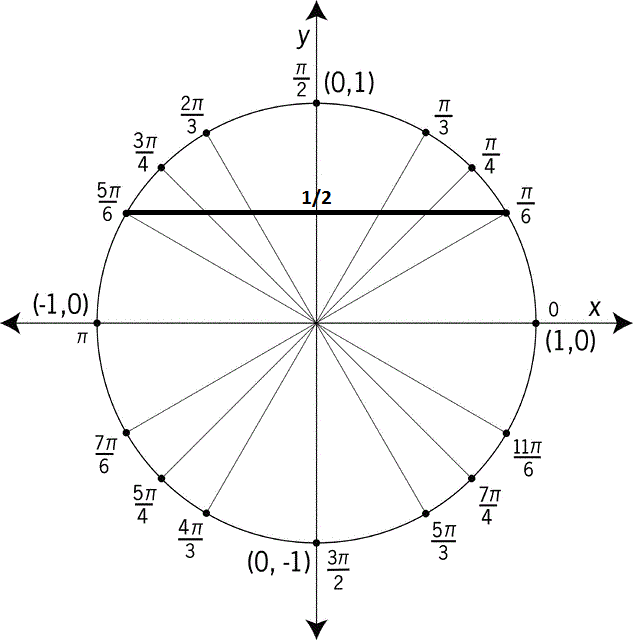
Если х [0; π], то х= π /6; х=5 π/6.

Если х [2 π;3 π], то х= π /6+2 π =13 π /6; х=5 π /6+2 π =17 π /6.

Если х [-π;-2 π], то х= π /6-2 π = -11 π /6; х=5 π /6-2 π = -7 π /6.

Вывод 1: если отрезок [0; π] переносим по оси х вправо на 2 π n,где n N, то значения углов увеличиваются на 2 π n; отрезок переносим влево на 2 π n, то значения углов уменьшаются на 2 π n.

Вывод 2 : этим свойством можно воспользоваться, если заданный отрезок вышел за пределы отрезка [0,2 π] .

б) Т(tg) = Т(ctg) = π n, где n N. Решаем аналогично разобранному примеру.

Пример: отобрать корни уравнения tgx=1 на отрезках [0; π]; [-π;0]; [π;2].

Если х [0; π], то х= π /4.

Если х [-π;0], то х= π /4 – π = -3 π /4.

Если х [π;2 π], то х= π /4 + π = 5 π /4.

Вывод 1 : заданный отрезок можем переносить вправо или влево по оси х на

π n,nN, тогда и значения углов будут меняться на π n.

Вывод 2: этим свойством можно воспользоваться, если заданный отрезок вышел за пределы отрезка [0;2 π]

7. Разрешение проблемы (учитель показывает оформление решений заданий – дети рассуждают).

Задание №1: отобрать корни уравнения sinх = -1/4 на отрезке [5 π /2;7 π /2] (проблемная ситуация из домашнего задания).

Решение:

1.Т(sin) = 2 π.

на -2 π

π /2 отбор корней 3 π /2 5 π /2 7 π /2

+ 2 π

2. Отбор корней на отрезке [π /2; 3 π /2] с помощью числовой окружности

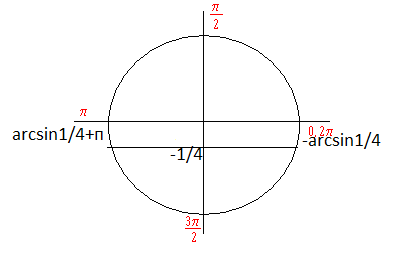
х = arcsin1/4 + π + 2 π = arcsin1/4 + 3 π.

Ответ : arcsin1/4 + 3 π.

Задание №2: отобрать корни уравнения cosx = 2/3 на отрезке [-5 π /2;-3 π /2].

Решение :

1.Т(cos) = 2 π.

на +2 π

-5 π /2 -3 π /2 - π /2 отбор корней π /2

-2 π

2. Отбор корней на отрезке [-π /2; π /2] с помощью числовой окружности

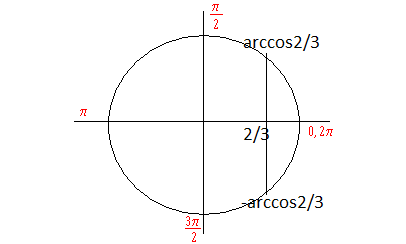
Ответ : arccos2/3 – 2 π; -аrcos2/3 – 2 π.

Задание №3 : отобрать корни уравнения tgx = 1/3 на отрезке [-7 π /4; - π /2].

Решение :

1. Т(tg) = 2 π.

на +2 π

-7 π /4 - π /2 π /4 отбор корней 3 π /2

-2 п

2. Отбор корней на отрезке [π /4;3 π /2].

х = arctg1/3 + π – 2 π = аrctg1/3 – π

Ответ : arctg1/3 – π.

8. Решение заданий по данной теме.

Отобрать корни уравнений на заданных промежутках :

а) sinx = 1/2 на [9 π /2;11 π /2]; б) cosx = -1/2 на [-5 π;-9 π /2];

в) tgx = 2 на [3 π /2;5 π /2].

9. Самостоятельная работа – 3 уровень проблемного обучения ( учащиеся пытаются выполнить задания самостоятельно, при необходимости учитель консультирует индивидуально) – слайд № 4.

10. Домашнее задание – 4 уровень проблемного обучения ( наличие любых типов проблем и полная самостоятельность в их решении): слайд №5.

11. Итог урока.

Цель – организовать анализ учебной деятельности на уроке.

Вопросы: 1. С помощью какого задания была создана проблемная ситуация ?

2. Какая возникла проблема ?

3. Как её разрешили ?

4. Какое свойство тригонометрических функций было использовано ?

5. Какие цели были поставлены ?

6. Достигли мы цели ?

Слайд № 6.