Урок разноуровневого обобщающего повторения по теме
«Тождественные преобразования тригонометрических выражений»
Цели: Обобщить теоретические знания по теме «Тождественные преобразования тригонометрических выражений», рассмотреть решение задач, связанных с этой темой, базового и повышенного уровней сложности. Организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных у них знаний. Способствовать усвоению основных формул тригонометрии в ходе решения задач.
Образовательная: Обеспечить в ходе урока закрепление следующих основных понятий: синус, косинус, тангенс и котангенс. Закрепить умение выполнять тождественные преобразования тригонометрических выражений, применяя основные тригонометрические тождества, формулы сложения, формулы двойного аргумента, формулы приведения. Продолжить формирование общеучебных умений и навыков:
планирование ответа;
навыки самоконтроля.
Контроль степени усвоения основных знаний, умений и навыков по данной теме.
Развивающая:
Развитие умений в применении знаний в конкретной ситуации.
Развитие логического мышления, умения выделять главное, проводить обобщение, делать верные логические выводы.
Развитие самостоятельной деятельности учащихся.
Воспитательная: Формирование научного мировоззрения, интереса к предмету через содержание учебного материала. Воспитание умения работать в коллективе, культуры общения, взаимопомощи. Воспитание таких качеств характера как настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.
Организационные формы урока: фронтальная, индивидуальная.
Вид урока: урок-практикум с использованием возможностей современных информационных технологий.
Используемое оборудование: компьютер, проектор, SMART-доска
Используемые ЦОР:
тренажеры из ЕКЦОР
карточки с заданиями
учебник “Алгебра и начала анализа 10” Ю.М.Колягин и др.;
рефлексия.
Ход урока
I этап урока – организационный (1 минута)
Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится у них на партах.
II этап урока - повторение изученного ранее материала (24 минуты).
Учитель. Прежде чем преобразовывать тригонометрические выражения, сначала повторим необходимые формулы (при повторение тригонометрических формул используется контроль 1 - 6. Эти задания учащиеся выполняют в тетрадях. Для проверки кто-то выходит к доске и вводит ответы. Очень хорошо это задание выполняется на интерактивной доске, дети могут поочередно выходить и “забивать” нужный ответ в соответствующую ячейку. Если ответ неправильный, то с помощью класса, записывается правильная тригонометрическая формула).
1. Формулы одного аргумента.
2. Формулы сложения.
3. Формулы двойного угла.
4. Формулы пониженной степени.
5. Формулы преобразования суммы в произведение.
6. Формулы приведения.
7. Знаки тригонометрических функций.

-
-
Учитель обращается к учащимся с вопросом: «Назовите основное тригонометрическое тождество и равенства, вытекающие из него».


Учитель: « Мы с вами вспомнили данные тождества. Теперь повторим формулы синуса и косинуса суммы и разности аргументов. А так же тангенса и сотангенса».
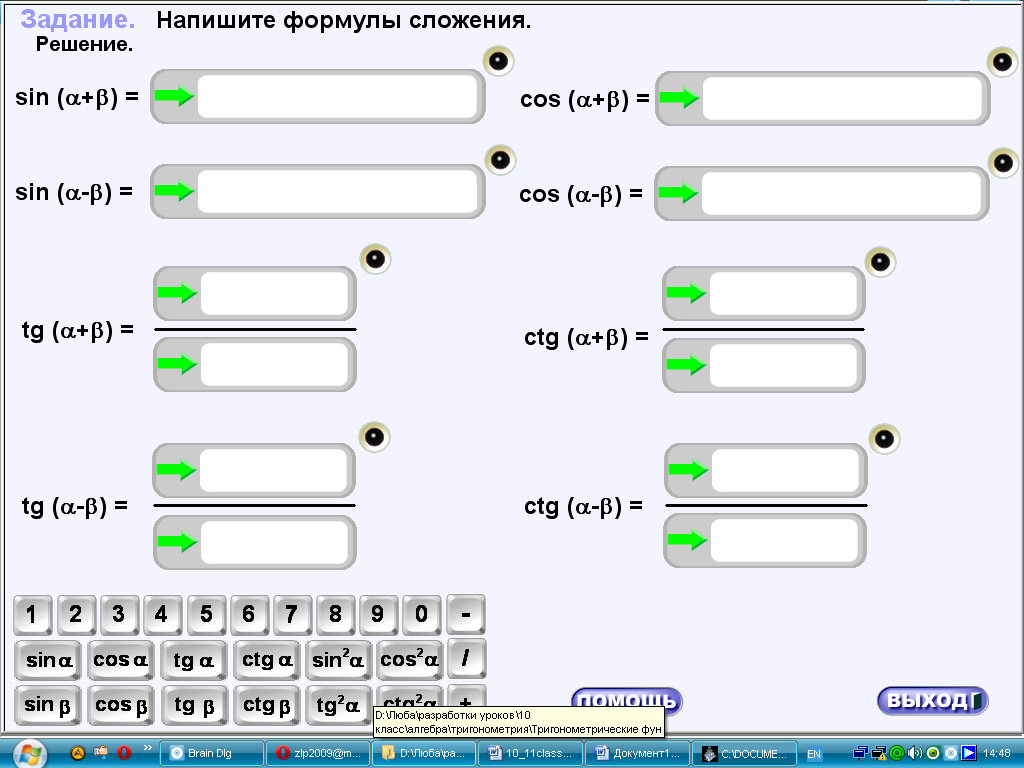

Учитель: «Давайте выполним практическое задание, на применение этих формул. У вас на столах лежат карточки с заданием № 1. Решаем это задание в рабочих тетрадях, а доске для самопроверки его выполняет один ученик».
Практическое задание № 1:
а) Упростить выражение:
1) sin3xcоs2х - 5 sin5x + cоs3xsin2х,
2) sin4xcоsх + 6cоs3х – cоs4xsinх,
3) 9 cоs9х + sin5xsin4х - cоs5хcоs4х,
4) 8,7cоs5,2хcоs0,8х – 0,7 cоs4,4x + 8,7sin5,2xsin0,8х,
5) 5sin2 x + 7 + 5cоs2 x,
6) -8 sin2 x - 12 - 8cоs2 x,
б) Найти значение выражения:
1) 3sin2 x + 5, если cоs2 x = 0,12,
2) cоs2 x - 14, если sinx = -0,3,
3) -3sinx + cоs2 x, если sinx = -1.
Ответы: а) 1) - 4 sin5x, 2) sin3x +6cоs3х, 3) 8 cоs9х, 4)8 cоs4,4x, 5)12, 6) -20; б) 1) 7,64, 2)-13,09, 3) 3.
Учитель: «А теперь вспомним не менее важные формулы двойного аргумента».


Учитель: «Выполним задание № 2 на применение данных формул».
Практическое задание № 2.
1) Упростить (устно):
а) 4cоs2 x sin2 x,
б) 6 cоs2 x +5 - 6sin2 x,
в)1+ cоs2x,
г) (cоs x – sin x)2,
д) 7 + sin2 4x – cоs2 4x .
Ответы: а) sin22x, б)5 + 6 cоs2x, в) 2cоs2 x, г) 1 - sin2x, д) 7 - cоs8x .
2) Найдите значение выражения
а) 5 sin2x, если cоs х = 0,6, -
б) - 2 cоs2x, если sin x = 0,7.
Ответы: а) - 4,8 , б) - 0,04.
Учитель: «Очень часто при преобразовании тригонометрических выражений применяются формулы приведения. Формул приведения очень много. Давайте вспомним алгоритм запоминания этих формул».
Учащиеся должны дать следующий ответ:
1) если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида  + α,
+ α,  – α , 2
– α , 2 + α , 2
+ α , 2 - α , то наименование тригонометрической функции следует сохранить;
- α , то наименование тригонометрической функции следует сохранить;
2) если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида  /2 + α ,
/2 + α ,  /2 – α , 3
/2 – α , 3 /2+ α , 3
/2+ α , 3 /2 - α, то наименование тригонометрической функции следует изменить (на родственное);
/2 - α, то наименование тригонометрической функции следует изменить (на родственное);
3) перед полученной функцией от аргумента α надо поставить тот знак, который имела бы преобразуемая функция при условии, что 0 /2.
Учитель: «Применим данное правило при решении задания № 3».
Практическое задание № 3:
а) Устно:


б) Упростите выражение и найдите его значение:
1) sin2(3 /2 – х) + cоs2(2
/2 – х) + cоs2(2 +х),
+х),
2) sinхsin(2 +х) - sin2(3
+х) - sin2(3 /2 – х),
/2 – х),
3) 4sin( + х)+ cоs(
+ х)+ cоs( /2 + х), если sinх = 0,5.
/2 + х), если sinх = 0,5.
4) tqx ·sin(3 /2 – x), если sinx = 1,4.
/2 – x), если sinx = 1,4.
Ответы: б) 1) 0, 2) cоs2х , 3) -2,5, 4) -1,4.
Учитель: «Мы с вами вспомнили основные тригонометрические формулы, формулы приведения, которые применяют для преобразования тригонометрических выражений. А теперь вспомним формулы преобразования суммы в произведение».


2
Учитель: Также вспомним формулы пониженной степени, которые также очень часто используются при упрощении тригонометрических выражений.

III этап урока - разно уровневая самостоятельная работа (15 минут)
Учитель выдает задания для самостоятельной работы, сообщая учащимся, что на ее выполнение отводится 15 минут. Учителем подготовлены карточки по уровням сложности.
«3» - № 2 обязательно, №№ 3,4 (из каждого номера по одному примеру, по выбору учащегося), №1 или №5 (упростить одно выражение)
«4» - №№ 1, 2 обязательно, №№ 3,4 (из каждого номера по два примера, по выбору учащегося), №5 (упростить любых два выражения)
«5» - любых 11 примеров (№2 обязательно).
I вариант
1. Упростите: ;
;
2. Найдите значение tg и ctg, если  , 90
, 90
3. Вычислите: а) sin 750; б) cos 810; в) tg450; г) ctg 390.
4. Найдите значение выражения: а) sin (-30); б) tg (-45); в) cos (-405).
5. Упростите: а) ; б)
; б) ; в)
; в) ; г) sin2 - (sin + cos)2; д)
; г) sin2 - (sin + cos)2; д) .
.
II вариант
1. Упростите: (sin - cos)2 + ( cos- sin)2-2
2. Найдите значение tg и ctg, если 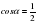 , 270
, 270
3. Вычислите: а) sin 420; б) cos 540; в) tg 405; г) ctg 1260.
4. Найдите значение выражения: а) sin (-45); б) ctg (-30); в) cos (-780).
5. Упростите: а) ; б)
; б) ; в)
; в) ; г)1- (sin + cos)2; д)
; г)1- (sin + cos)2; д)  .
.
Дополнительно:
Вычислить:
sin 575·cos845- cos1405·sin1675- tg215· tg685- tg235;
4sin18·sin306.
По истечении времени учащиеся сдают работы.
IV этап урока - подведение итогов урока, комментарии по домашнему заданию (5 минут)
Учитель еще раз обращает внимание на те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Оценивает работу отдельных учащихся на уроке, при необходимости выставляет отметки.
В качестве домашнего задания учащиеся получают варианты диагностической контрольной работы (Проверь себя).








 /2 – х) + cоs2(2
/2 – х) + cоs2(2







 + α,
+ α, 




 ;
;  , 90
, 90 ; б)
; б) ; в)
; в) ; г)
; г)  .
.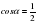 , 270
, 270 ; б)
; б) ; в)
; в) ; г)1- (
; г)1- ( .
.









