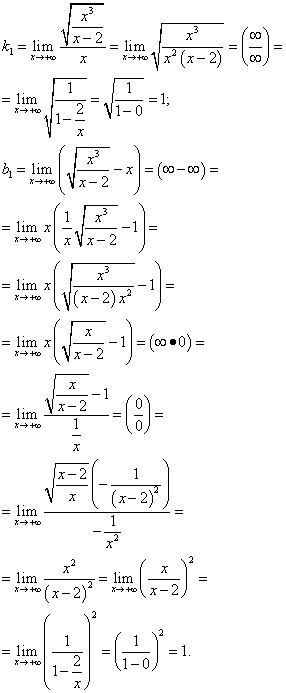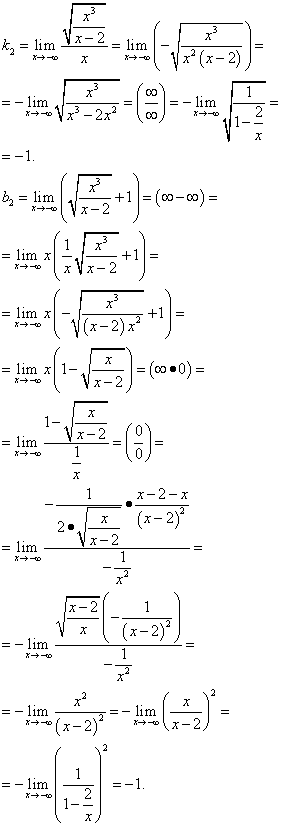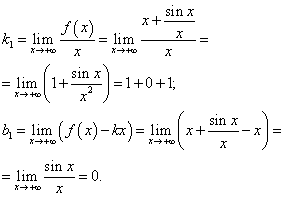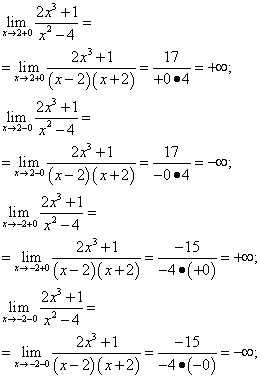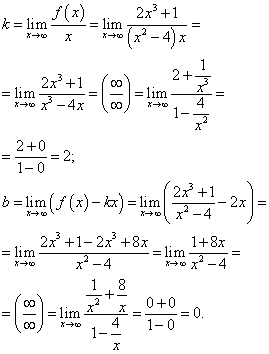Урок на тему "Асимптоты"

Тема урока: Асимптоты функции, их виды и нахождение.

Цели урока:1.Обучающая: Рассмотреть виды асимптот функции и способы их нахождения. 2.Развивающая: Способствовать развитию логического мышления, памяти.    3. Воспитательная: Аккуратное ведение конспектов, самодисциплина.     

 : Урок изучения нового материала и первичного закрепления.

. I. Оргмомент

II. Актуализация опорных знаний        Устный опрос.

 II. Целевая установка.

Ход урока. 1. Тема урок

2. Цель урока III. Формирование новых понятий и способов действий.  Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если  выполнено хотя бы одно из условий:,  Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞,  если  Аналогично определяются горизонтальная и наклонная асимптоты при x →–∞. Для того, чтобы прямая y = kx + b была асимптотой графика функции y = f (x) при x → +∞,  необходимо и достаточно, чтобы существовали конечные пределы

IV.  Формирование навыков умственного труда

 Пример 1.  Для функции  найти асимптоты. Решение График   условие  имеет вертикальную асимптоту х = 1, поскольку при   выполняется  , а также при   выполняется условие  . Вертикальная асимптота функции Пример 2. Найти асимптоты графика функции: 

Решение 1) х = 1 – вертикальная асимптота

2) Найдём наклонные асимптоты графика  ,  ,  ­ уравнение наклонной асимптоты. График   и его наклонная асимптота Пример 3. Найти асимптоты графика функции:  Решение Таким образом, при  Теперь найдём асимптоту при  . Имеем:   наклонной асимптотой служит прямая , уравнение наклонной асимптоты при  будет: График   и его две наклонных асимптоты V. Итог  урока.       Подведение итогов, выводы.

Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.

Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.

Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.

Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.

Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты

Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy.

Определение. Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.

Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:

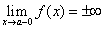•  (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)

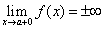•  (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).

При этом функция f(x) может быть вообще не определена соответственно при x ≥ a и x ≤ a.

Замечание:

• символом 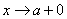  обозначается стремление x к a справа, причём x остаётся больше a;

• символом 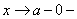  обозначается стремление x к a слева, причём x остаётся меньше a.

Из сказанного следует, что вертикальные асимптоты графика функции можно искать не только в точках разрыва, но и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.

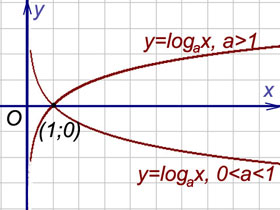
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:

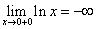
(рис. сверху).

Найти асимптоты графика функции самостоятельно

Пример 2. Найти асимптоты графика функции  .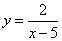

Пример 3. Найти асимптоты графика функции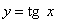 

Пример 4. Найти асимптоты график функции  .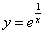

Горизонтальные асимптоты

Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox.

Если 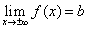  (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b), то y = b – горизонтальная асимптота кривой y = f(x) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).

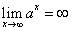
Наклонные асимптоты

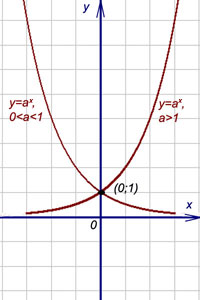
Пример 5. График функции

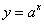
при a  1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox), так как предел функции при стремлении "икса" к минус бесконечности равен нулю:

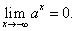
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении "икса" к плюс бесконечности равен бесконечности:

Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число - точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше - угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё - уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.

Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:

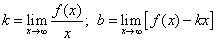          (1)

и

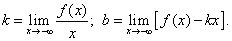      (2)

Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.

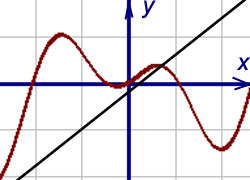
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.

При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

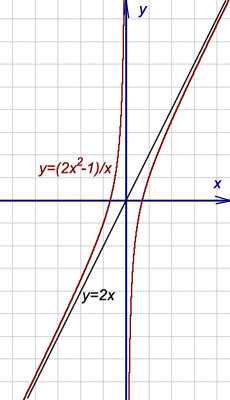
Пример 6. Найти асимптоты графика функции

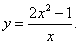
Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.

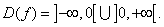
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:

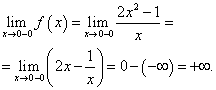
Следовательно, x = 0 – вертикальная асимптота графика данной функции.

Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:

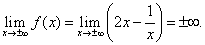
Выясним наличие наклонной асимптоты:

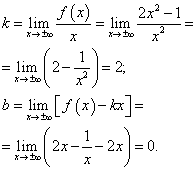
Получили конечные пределы k = 2 и b = 0. Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).

Пример 7. Найти асимптоты графика функции

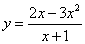
Решение. Функция имеет одну точку разрыва x = −1. Вычислим односторонние пределы и определим вид разрыва:

,

.

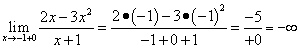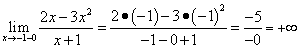Заключение: x = −1 - точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.

Ищем наклонные асимптоты. Так как данная функция - дробно-рациональная, пределы 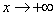при   и при 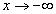  будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой - наклонной асимптоты:

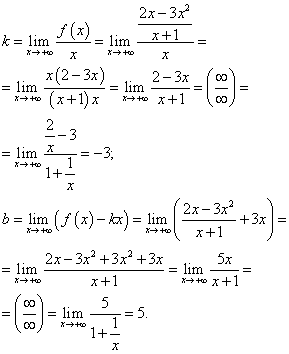
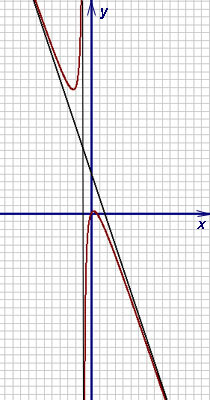
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:

y = −3x + 5.

Пример 8. Найти асимптоты графика функции

.

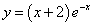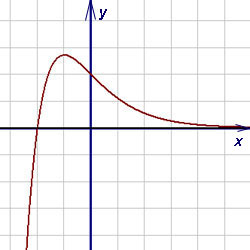
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:

.

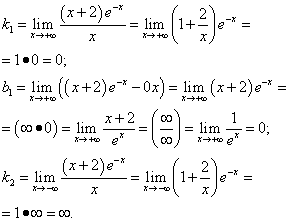Таким образом, график данной функции имеет асимптоту y = 0 при 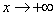  и не имеет асиптоты при  .

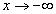Пример 9. Найти асимптоты графика функции

.

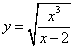Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство 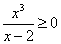  и при этом  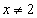. Знак переменной x совпадает со знаком  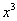. Поэтому рассмотрим эквивалентное неравенство  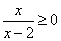. Из этого получаем область определения функции:  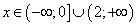. Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0.

Рассмотрим правосторонний предел при 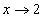  (левосторонний предел не существует):

.

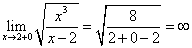Точка x = 2 - точка разрыва второго рода, поэтому прямая x = 2 - вертикальная асимптота графика данной функции.

Ищем наклонные асимптоты:

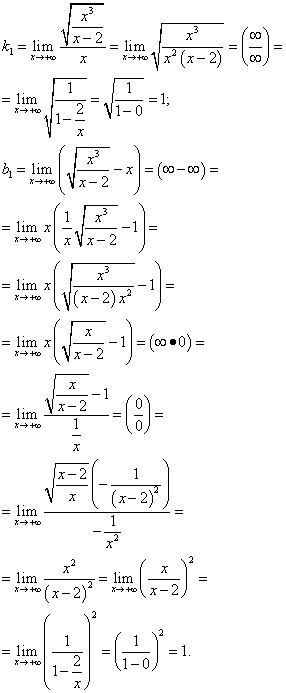
Итак, y = x + 1 - наклонная асимптота графика данной функции при 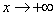 . Ищем наклонную асимптоту при  :

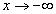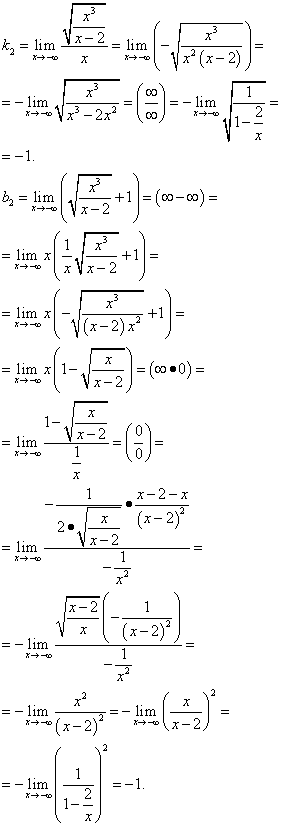
Итак, y = −x − 1 - наклонная асимптота при  .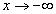

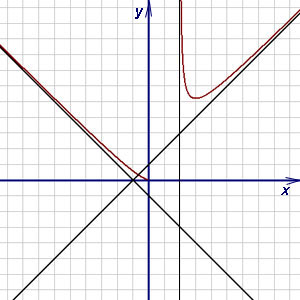
Пример 10. Найти асимптоты графика функции

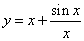
Решение. Функция имеет область определения 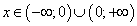 . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при  :

,

.

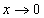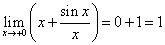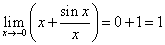Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 - точка устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.

Ищем наклонные асимптоты: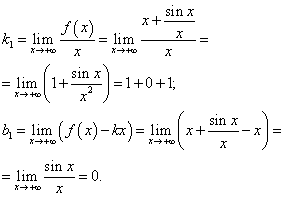

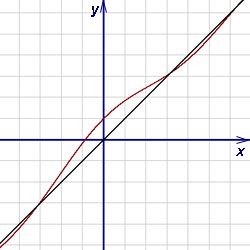
Таким образом, при 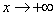  наклонной асимптотой графика данной функции является прямая y = x. Но при  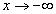 найденные пределы не изменяются. Поэтому при  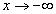 наклонной асимптотой графика данной функции также является y = x.

Пример 11. Найти асимптоты графика функции

.

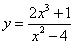Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие 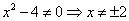 . Функция имеет две точки разрыва:  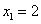,  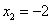. Чтобы установить вид разрыва, найдём односторонние пределы: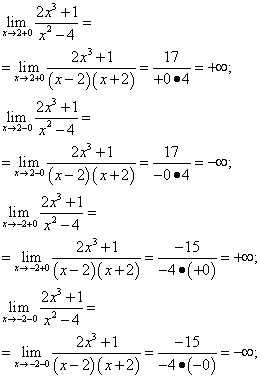

Так как все пределы равны бесконечности, обе точки разрыва - второго рода. Поэтому график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2.

Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы 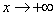при   и при 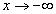  совпадают. Поэтому, определяя коэффициенты прямой, ищем просто пределы:

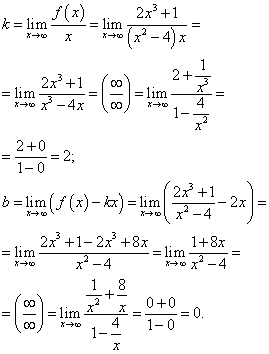
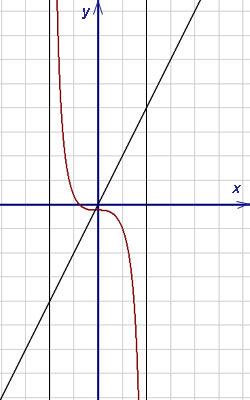
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x. Таким образом, график данной функции имеет три асимптоты: x = 2, x = −2 и y = 2x.

Найти асимптоты графика функции самостоятельно

Пример 12. Найти асимптоты графика функции  .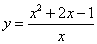

Пример 13. Найти асимптоты графика функции 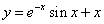 .
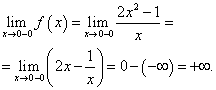
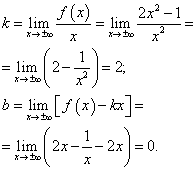
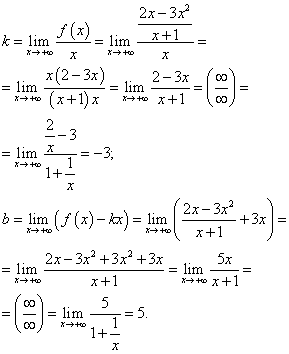
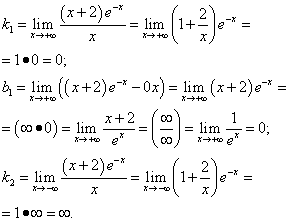