Россия, Злынка
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 23.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 16.05.2025 13:19
Тышкевич Елена Викторовна
Преподаватель математики и информатики
36 лет
519
94 200 
Местоположение
Урок на тему: "Приближенные вычисления"
Категория:
Математика
18.05.2022 21:41
Просмотр содержимого документа
«Урок на тему: "Приближенные вычисления"»
Тема урока: «Приближенные вычисления»
Цели урока:
- образовательные:
-
закрепить навыки округления действительных чисел:
-
дать понятие приближенного значения величины.
- развивающиеся:
Ход урока
1.Организационный этап: взаимное приветствие; проверка подготовленности студентов к уроку.
1. Округлите до сотых число:
а) 6,113; в) 1,407; д) 2,5013;
б) 0,318; г) 10,275; е) 11,096.
3. Сократите дробь: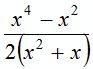 
.
3. Изучение новой темыс использованием презентации:
3.1. Приближенные вычисления. Рассказ преподавателя с использованием презентации. Краткая запись в тетрадь.
1. При решении практических задач часто приходится иметь дело с приближенными значениями различных величин.
2. Привести примеры из жизни, где используются точные и приближенные величины.
3. Если известно точное и приближенное значение величины, то полезно знать, на сколько приближенное значение отличается от точного, т. е. какова погрешность приближения.
4. Модуль (абсолютная величина) разности между значениями величины и ее приближенным значением называют абсолютной погрешностью приближения.
5. Обозначим точное значение величины буквой х, а приближенное – буквой а. Тогда погрешность приближения равна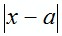 
.
Приближенные вычисления.
Погрешностью приближенного значения а числа х называется разность х-а между числом х и этим приближенным значением а. Обозначается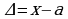 
.
Абсолютной погрешностью приближенного значения а числа х называется модуль погрешности этого приближения: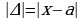 
.
Относительной погрешностью приближенного значения а числа х (а≠0, х≠0) называется отношение абсолютной погрешности этого приближения к модулю числа а.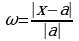 
.
Пример 1. Приближение числа 3,24 равно 3,2. Вычислить абсолютную и относительную погрешности приближения.
Решение: Абсолютная погрешность равна |3,24-3,2|=0,04. Относительная погрешность равна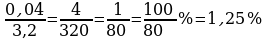 
Пример 2 (на доске вместе). Известно приближение числа 6,45: а) 6,4; б) 6,5. Вычислите абсолютную и относительную погрешности каждого приближения.
Округление чисел.
Пример. Округлить число 7,40952 последовательно до единиц, десятых долей, сотых долей, тысячных долей.
4. Закрепление материала:
4.1. № 5.1-5.5, 5.13-5.15, 5.22,
4.2. Задания на слайдах.
1) 
;
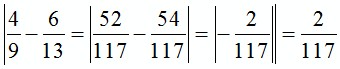3) 
.
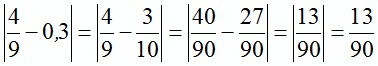№ 1 (1, 3).
1) 
;
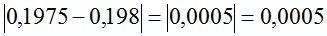3) 
.
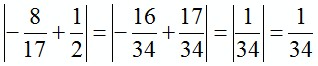№ 2 (1; 3).
1) 
;
3) 
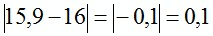. Ответ: 
.
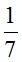№ 3
,
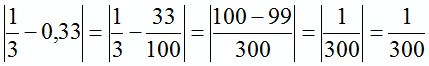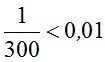. Ответ: верно.
№ 4
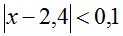. Это неравенство можно записать в виде двойного:
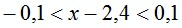или в виде системы:
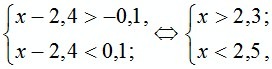т. е.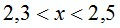 
. Ответ: .
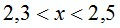5. Итог урока. Рефлексия.
6. Домашнее задание: стр.13 - 16 учебник Башмаков М.И
© 2022, Тышкевич Елена Викторовна 872 42
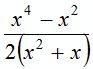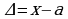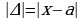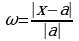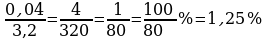
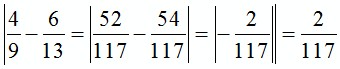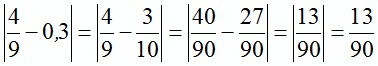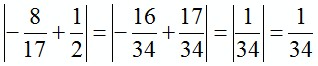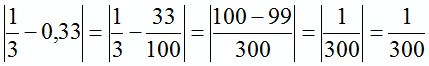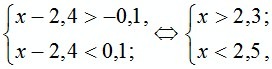Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
