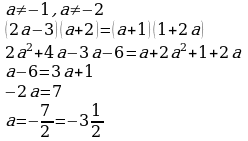| II Мотивация
| -Создатель теории относительности Альберт Эйнштейн в свое время заметил: «Мне приходится делить свое время между политикой и уравнениями. Однако, уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
Что вы извлекли из данных слов?
Что такое уравнение?
Что значит решить уравнение?
|
Что уметь решать уравнения важно. Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти.
Решить уравнение - значит найти все его корни или доказать, что корней нет | Коммуникативные: уметь выражать свои мысли с достаточной точностью и полнотой |
| III. Устная работа
| Какие уравнения вы видите на слайде? 
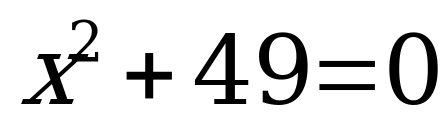
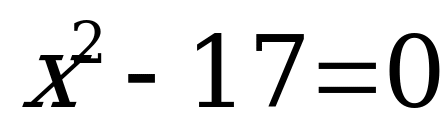
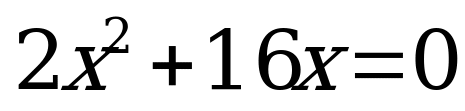
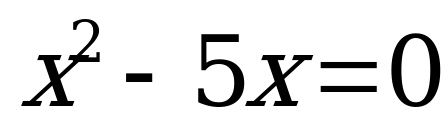
Какие теперь уравнения вы видите на слайде? 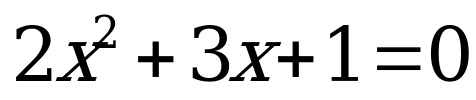 , ,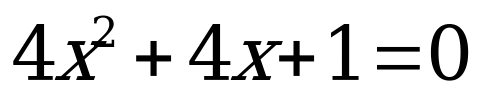 , , 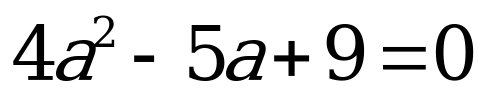
Как узнать, сколько корней имеет уравнение?
Какие уравнения вы уже умеете решать?
Какое уравнение называется целым?
Скажите, в каких случаях целое уравнение имеет смысл?
Дробное выражение при некоторых значениях переменной может не иметь смысла.
Назовите область допустимых значений переменной в выражении 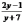 ; ; 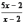 ; ; 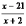

Итак, ребята, мы с вами знакомы с линейными, квадратными уравнениями и пришло время научиться решать новый вид уравнений дробные рациональные.
| Неполные квадратные
Полные квадратные.
Найти дискриминант
Линейные, квадратные полные и квадратные неполные, целые рациональные.
Целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения
Целое выражение имеет смысл при любых значениях входящих в нее переменных.
Допустимыми значениями переменной являются все значения, кроме…
| Познавательные: структурирование собственных знаний.
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: контроль и оценка процесса и результатов деятельности.
Личностные: оценивание усваиваемого материала |
| IV Сообщение темы урока, постановка целей урока.
| Сформулируйте тему урока.
ЦЕЛЬ: познакомить с новым видом уравнений - дробными рациональными уравнениями, дать представление об алгоритме решения дробных рациональных равнений.
это надо людям, которые свяжут свою жизнь с наукой (физики, математики, программисты, инженеры и т. д.), в быту же эти уравнения, как и 80% всей математики нужны только для развития логики | Решение дробных рациональных уравнений. Научиться… Узнать…
Записывают в тетрадь дату, определяют тему и цели урока.
| Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме.
Личностные: самоопределение.
Регулятивные: целеполагание.
Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. |
| V. Изучение нового материала
VI. Закрепление.
VII. Обобщение, подведение итогов
VIII..Контроль и самопроверка знаний. Цель: проверить усвоение полученных знаний и умений, обсудить допущенные ошибки.
IX. Информация о домашнем задании. Цель: обеспечение понимания детьми содержания и способов выполнения домашнего задания
X I.Рефлексия. Цель: обеспечение осознания учащимися своей учебной деятельности на уроке. Соотнесение цели урока и результата.
| Ребята, давайте вспомним алгоритм решения целых уравнений.
Найти общий знаменатель Умножить обе части уравнения на общий знаменатель Решить полученное уравнение
Но целое рациональное отличается от дробного рационального, тем, что есть деление на выражение с переменными. Значит в алгоритм решения добавляется еще один пункт. Исключить из его корней те, которые обращают в нуль общий знаменатель.
Потренируемся находить общий знаменатель. 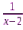 и и 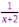
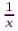 и и 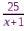
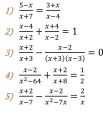
Учебник. Стр. 134 Итак, мы продолжаем отрабатывать навык решения дробных рациональных уравнений и не забываем, что решение уравнений одно из заданий ОГЭ.
Определите, какие из чисел 4, 0, -2 являются корнями уравнения. Ответы поясните. 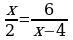
в) Перед вами решение уравнения. Но оно выполнено с ошибкой. Ваша задача: найти, какой шаг алгоритма нарушен, и назовите его правильное решение. Найди ошибку (слайд) (3мин) 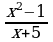 - - 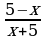 =0; =0;
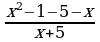 =0 =0
ОДЗ : х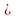 -5 -5 х2-х+6=0, D = 1+24=25, D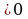 , 2-корня , 2-корня х1 =3, х2 = -2. Ответ :-2; 3
Найдите общий знаменатель и определите дополнительный множитель каждой дроби. Определить какие числа не могут быть корнями уравнений 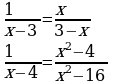 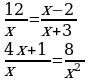
Учитель проверяет ответы и дает соответствующие пояснения.
Какое уравнение называют дробным рациональным? Сформулируйте алгоритм решения дробного рационального уравнения.
Самостоятельно: 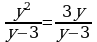
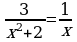 ; ;
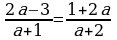
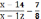 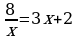
Исторический материал об Омаре Хайяме.
Омар Хайям – математик и поэт Одни их крупнейших средневековых алгебраистов был персидский и таджикский ученый и поэт Омар Хайям (1048-1131). Он родился в семье ремесленника в городе Нишапуре (ныне Северный Иран), к югу от Ашхабада, жил и работал в Самарканде, Исфахане и других городах Средней Азии и Ирана. Когда он был еще молодым, большая часть Среднего Востока была захвачена сельджуками. Положение честных ученых, которых преследовали властители, было крайне тяжелым. В молодости Омар Хайям увлекался астрономией и математикой, позже в нем пробудился интерес к географии, философии и поэзии. Всему миру известны его знаменитые стихи – рубаи (не склоняемое существительное). Вот одно из них. …Мне мудрость не чуда была земная, Разгадки тайн ища, не ведал сна я. За 70 перевалило мне, что ж я узнал? Что ничего не знаю.
Первое его математическое сочинение – “Трудности арифметики” - до нас не дошло. Благодаря материальной помощи, оказанной ему одним самаркандским меценатом, Хайям смог продолжить свои научные исследования и написать важнейший труд – “О доказательстве задач алгебры и алмукабалы”. Эта книга содержала почти всю совокупность алгебраических знаний того времени. В ней дается классификация уравнений и излагается решение уравнений первой, второй и третьей степени. Во введении автор утверждает, что алгебра – это наука об определении неизвестных величин, состоящих в некоторых отношениях с величинами известными. Определение неизвестных осуществляется с помощью составления и решения уравнений. Это первое дошедшее до нас определение алгебры как науки. Алгебра Хайяма часто словесная.
Предлагаю решить уравнение, которое формулируется у Хайяма следующим образом: “Доля квадрата равна половине доли квадрата”. В современных обозначениях эта задача выглядит так: Решить уравнение. 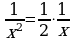 и №600(и), № 602(б) и №600(и), № 602(б)
Чему вы научились сегодня на уроке? Что стали делать лучше? В чем разобрались? Что еще не совсем хорошо получается? Что труднее всего дается?
|
Решают уравнения на доске и в тетради.
Учащиеся: 4 не может быть корнем, т.к. знаменатель обращает в нуль. 0 не является корнем, т.к. 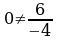 . . -2 является корнем, т.к. 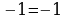
Учащиеся решают. Правильный ответ 2 ; -3.
У доски учащиеся решают 8-10 мин предложенные уравнения на досках Остальные работают на местах. Учащиеся, владеющие навыками решения дробно-рациональных уравнений решают самостоятельно. 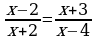 ; ;
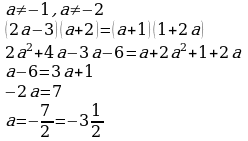
Учащиеся записывают в дневники задание |
Познавательные: формирование интереса к данной теме.
Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других.
Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата.
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Познавательные: формирование интереса к данной теме.
Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме, слушать и понимать речь других.
Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. Личностные: формирование позитивной самооценки, учатся принимать причины успеха (неуспеха). Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений. Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы.
Регулятивные: уметь правильно оценивать собственную деятельность на уроке. .
|






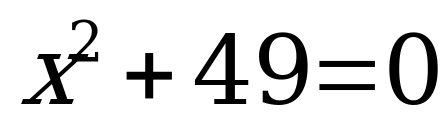
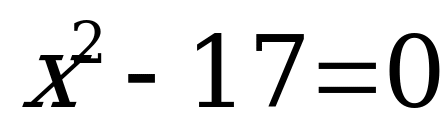
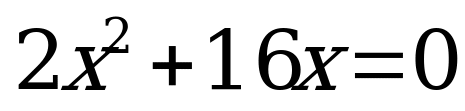
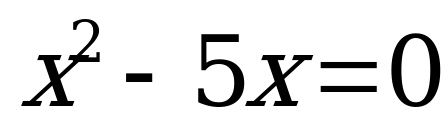
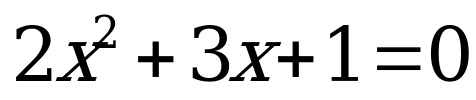 ,
,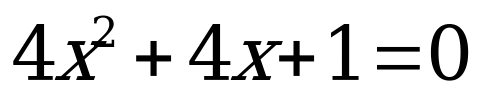 ,
, 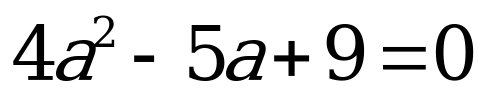
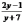 ;
; 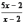 ;
; 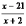

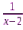 и
и 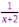
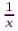 и
и 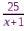
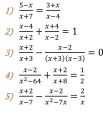
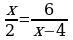
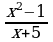 -
- 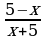 =0;
=0; 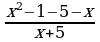 =0
=0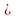 -5
-5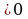 , 2-корня
, 2-корня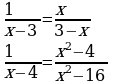
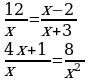
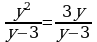
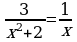 ;
; 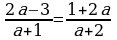
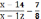
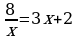
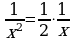 и №600(и), № 602(б)
и №600(и), № 602(б)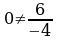 .
. 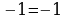
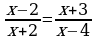 ;
;