Урок по алгебре в 9 классе "Теория вероятности в задачах ОГЭ"

Открытый урок в 9 классе проведён учителем математики РМЛИ ДОД Колодяжной Еленой Михайловной.

Тема урока:

Теория вероятностей в задачах ГИА.

Цель урока:

Сформировать навыки решения задач на вероятность.

З адачи урока:

Дать представление о том, какие задания могут быть в вариантах ГИА по теории вероятности. Помочь учащимся при подготовке к экзамену.

Оборудование:

интерактивная доска, презентация.

ХОД УРОКА:

I. Организационный момент.

- Здравствуйте, ребята! Сегодня на уроке мы будем разбирать задачи по теории вероятности. Просто, понятно и доступно. Здесь не будет такой математической строгости, как в учебнике. Многие понятия мы дадим на интуитивном уровне. Самое главное – это практика. Мы разберём большое количество задач и тогда на экзамене вы сможете решить любую задачу по теории вероятности.

- Откройте тетради, запишите число и тему урока. (Слайд 1)

- Наш урок состоит из трёх основных этапов: исторического, этапа повторения и изучения нового материала. А начнём мы с введения. (Слайд 2)

II. Введение. Что изучает теория вероятности?

- Наша жизнь полна случайностей: землетрясения, ураганы, подъёмы и спады в экономике, случайные встречи и т.д. Исходы многих явлений заранее предсказать невозможно. Например, нельзя сказать наверняка какой стороной упадёт подброшенная вверх монета, когда в следующем году выпадет первый снег. Такие непредсказуемые явления называются случайными.

Событие, которое может произойти, а может не произойти, называется случайным.

Раздел математики, изучающий случайные события, их свойства и операции над ними, называется теорией вероятностей. (Слайд 2)

- Запишите определения в тетрадь.

- Области применения теории вероятности обширны. Помимо математики, это физика, астрономия, биология, геодезия, теория стрельбы. Теория вероятности помогает определить количество брака на производстве, погрешность в статистике, экономике и многом другом.

При решении задач всё сами увидите.

I II. Из истории.

Развитие теории вероятностей начиналось весьма своеобразно...

Первоначальным толчком послужили задачи, относящиеся к азартным играм в кости и карты ( в переводе с французского «азарт» (le hazard) означает «случай»). (Слайды 3, 4)

В о время многочасовых игр замечались определённые закономерности (некоторые комбинации карт или костей появляются чаще других).

Возникли вопросы:

1) Сколько раз надо бросить кости, чтобы получить наибольшее число очков?

2) Каким образом разделить ставку между игроками в случае, если игра не была окончена?

Игроки обратились к математикам в надежде узнать от них выигрышную стратегию. И математики стали подсчитывать различные вероятности в азартных играх. (Слайд 5)

Основателями теории вероятностей были французские математики 17 в. Блез Паскаль, Пьер Ферма и голландский ученый Христиан Гюйгенс. (Слайд 6)

В 1657 г. появилась работа Х.Гюйгенса «О расчетах в азартных играх».

Т рактат выдержал несколько изданий и до начала 18 в. был единственным руководством по теории вероятностей. (Слайд 7)

Но как математическая наука теория вероятностей начинается с работы выдающегося швейцарского математика Якоба Бернулли (1654 – 1705).

В трактате «Искусство предположений» (1713 г.) он ввёл значительную часть современных понятий теории вероятностей и доказал ряд теорем. (Слайд 8)

Классическое определение вероятности было впервые дано в работах французского математика Пьера Симона Лапласа (1749 – 1827).

(Слайд 9)

Особенно быстро теория вероятностей развивалась во второй половине 19 в. и 20 в. В этот период фундаментальные открытия были сделаны математиками Петербургской школы

П.Л.Чебышёвым, А.М.Ляпуновым, А.А.Марковым. (Слайд 10)

С трогое логическое обоснование теории вероятностей произошло в 20 в. и связано с именами советских математиков С. Н. Бернштейна (1880 – 1968) и А. Н. Колмогорова (1903–1987).

Они разработали аксиоматику, которая в настоящее время является общепринятой. (Слайд 11)

IV. Повторение.

- Напомните мне, что изучает теория вероятностей? (Случайные события.)

- Как найти вероятность случайного события? (Вспомните классическое опр-е Лапласа.)

Классическое определение вероятности (по Лапласу):

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

, где

P – обозначение происходит от первой буквы французского слова probabilite – вероятность.

(Слайды 12, 13)

- Рассмотрим несколько устных задач на применение этого определения.

Задача №1

Дежурные по классу Алексей, Иван, Татьяна и Ольга бросают жребий - кому стирать с доски. Найдите вероятность того, что стирать с доски достанется одной из девочек.

(Слайд 14)

Задача №2

Из слова ЭКЗАМЕН случайным образом выбирают букву. Какова вероятность того, что она окажется гласной?

(Слайд 15)

Задача №3

Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

(Слайд 16)

Задача №4

В среднем из 1000 компьютеров, поступивших в продажу, 25 неисправны. Какова вероятность купить исправный компьютер?

(Слайд 17)

Задача №5

В некотором городе из 4000 появившихся на свет младенцев 1950 девочек. Найдите частоту рождения мальчиков в этом городе. Результат округлите до тысячных.

(Слайд 18)

Задача №6

В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски и по-английски. Какова вероятность того, что случайно выбранный турист говорит хотя бы на одном иностранном языке?

(Слайд 19)

Задача №7

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

(Слайд 20)

Задача №8

В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом разбивают на 2 группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

(Слайд 21)

Задача №9

На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

(Слайд 22)

Задача №10

Игральный кубик бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4.

(Слайд 23)

Задача №11

В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность того, что выпадет четное число.

(Слайд 24)

Задача №12

В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность того, что выпадет число, отличающееся от числа 3 на единицу.

(Слайд 25)

Задача №13

В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков.

(Слайд 26)

Задача №14

В случайном эксперименте бросают два игральных кубика. Какая сумма очков наиболее вероятна?

(Слайд 27)

Задача №15

Игральный кубик бросают дважды. Найдите вероятность того, что первый раз и во второй раз выпадет одинаковое число очков.

(Слайд 28)

Задача №16

В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет меньше 5 очков.

(Слайд 29)

Задача №17

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что ОРЕЛ выпадет ровно один раз.

(Слайд 30)

Задача №18

Монету бросают дважды. Найдите вероятность того, что выпадет хотя бы один ОРЕЛ.

(Слайд 31)

Задача №19

Монету бросают дважды. Найдите вероятность того, что ОРЕЛ не выпадет ни разу.

(Слайд 32)

Задача №20

В случайном эксперименте монету бросили три раза. Какова вероятность того, что ОРЕЛ выпал ровно два раза.

(Слайд 33)

Задача №21

Монету бросают три раза. Какова вероятность того, что результаты двух первых бросков будут одинаковы?

(Слайд 34)

Задача №22

Монету бросают три раза. Найдите вероятность того, что результаты первого и последнего броска различны.

(Слайд 35)

Задача №23

Монету бросают четыре раза. Найдите вероятность того, что ОРЕЛ выпадет ровно три раза.

(Слайд 36)

V. Новый материал.

Основные понятия:

События, которые не могут происходить одновременно, называются несовместными.

События, которые происходят независимо друг от друга, называются независимыми.

(Слайды 37, 38)

Сумма и произведение событий:

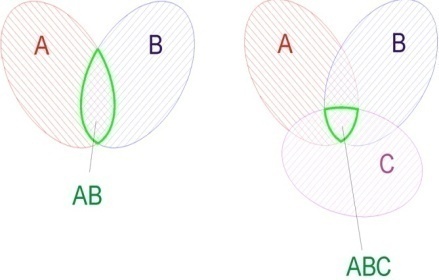
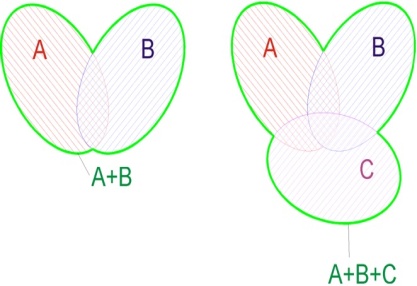
Если А и В несовместные, то

Если А и В независимые, то

(Слайд 39)

- Разберём несколько задач на применение этих понятий.

Задача №1

На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,25. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

(Слайд 40)

Задача №2

В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

(Слайд 41)

Задача №3

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55% . Первая фабрика выпускает 3 % бракованных стекол, а вторая — 1% . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

(Слайд 42)

Задача №4

Вероятность того, что на тесте по математике учащийся Д. верно решит больше 11 задач, равна 0,67. Вероятность того, что Д. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что Д. верно решит ровно 11 задач.

(Слайд 43)

Задача №5

Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедель- ник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятость того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.

(Слайд 44)

Задача №6

Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

(Слайд 45)

Задача №7

Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а послед- ние 2 раза промахнулся. Результат округлите до сотых.

(Слайд 46)

Задача №8

В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероят- ностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

(Слайд 47)

Задача №9

Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

(Слайд 48)

Задача №10

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

(Слайд 49)

Задача №11

Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

(Слайд 50)

Задача №12

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

(Слайд 51)

Задача №13

Маша коллекционирует принцесс из Киндер – сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, т.е. в каждом очередном Киндер – сюрпризе может с равными вероятностями оказаться любая их 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придется купить еще 2 или 3 шоколадных яйца?

(Слайд 52)

VI. Итог урока.

1. С какими задачами мы сегодня работали на уроке?

2. В чём их особенность?

3. Какие методы их решения мы рассмотрели на уроке?

VII. Домашнее задание.

1. В чемпионате по прыжкам в воду участвуют 7 спортсменов из России, 6 из Китая, 3 из Кореи, 4 из Японии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что первым будет выступать спортсмен из России.

2. Вероятность того, что шариковая ручка пишет плохо (или не пишет) равна 0,1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что ручка пишет хорошо.

3. В среднем из 1600 садовых насосов, поступивших в продажу, 8 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

4. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

5. В сборнике билетов по истории всего 60 билетов, в 18 из них встречается вопрос по смутному времени. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по смутному времени.

6. В соревнованиях по толканию ядра участвуют 20 спортсменов, среди них 2 спортсмена из Испании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что девятым будет выступать прыгун из Испании.

7. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 36 шашистов, среди которых 15 участников из России, в том числе Евгений Коротов. Найдите вероятность того, что в первом туре Евгений Коротов будет играть с каким-либо шашистом из России?

8. Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.

9. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

10. Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,14. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

11. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

12. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 95% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 15% яиц высшей категории. Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

13. Какова вероятность того, что случайно выбранное натуральное число от 67 до 88 делится на 2?

14. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 8 очков в двух играх. Если команда выигрывает, она получает 7 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

15. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Протор» по очереди играет с командами «Стратор», «Монтёр» и «Стартер». Найдите вероятность того, что «Протор» будет начинать только первую и последнюю игры.

16. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.