Урок по математике (внеурочное занятие) на тему: "Мир правильных многогранников"

Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.

Бертран Рассел

ПРАВИЛЬНЫЙ МНОГОГРАННИК-

выпуклый многогранник,

грани которого являются правильными

многоугольниками с одним и тем же числом сторон

и в каждой вершине которого сходится одно и то же число ребер.

Икосаэдр

Тетраэдр

Октаэдр

Гексаэдр

Додекаэдр

«эдра» - грань

«тетра» - 4

«гекса» - 6

«окта» - 8

«икоса» - 20

«додека» - 12

ТЕТРАЭДР

Тетраэдр – представитель правильных выпуклых многогранников.

Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой вершине по три.

КУБ (ГЕКСАЭДР)

Куб или гексаэдр – представитель правильных выпуклых многогранников.

Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.

ОКТАЭДР

Октаэдр – представитель семейства правильных выпуклых многогранников.

Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре.

ДОДЕКАЭДР

Додекаэдр – представитель

семейства правильных выпуклых многогранников.

Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три.

ИКОСАЭДР

Икосаэдр – представитель семейства правильных выпуклых многогранников.

Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять.

тетраэдр

огонь

икосаэдр

вода

октаэдр

воздух

гексаэдр

земля

додекаэдр

вселенная

1 группа- доказать, что правильных многогранников

существует ровно 5.

2 группа- используя модели многогранников,

заполнить данную таблицу и сделать вывод.

3 группа- вывести формулы для нахожденияплощадей

поверхности прав. многогранников.

4 и 5 группы- составить развёртки правильных

многогранников.

Вывод:

Существует лишь пять выпуклых правильных многогранников –

тетраэдр , октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями

Правильный многогранник

Число

граней

  Тетраэдр 

  Куб  

вершин

4

6

  Октаэдр  

4

рёбер

6

8

  Додекаэдр  

8

12

6

12

  Икосаэдр

12

20

20

30

12

30

Правильный многогранник

Число

граней и вершин

(Г + В)

  Тетраэдр  

рёбер

(Р)

8

  Куб 

  Октаэдр  

14

6

12

  Додекаэдр  

14

12

32

  Икосаэдр

30

32

30

Теорема Эйлера

Число вершин плюс число гра ней минус число рёбер равно двум.

В + Г – Р = 2

Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик

Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.

• Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр.

• Два из них знал

И. Кеплер (1571 – 1630 гг.).

• В 1812 году французский математик О. Коши
• доказал, что кроме пяти «платоновых тел» и
• четырех «тел Пуансо» больше нет
• правильных многогранников.

Малый звездчатый

додекаэдр

Большой звездчатый

додекаэдр

Большой икосаэдр

Большой додекаэдр

Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук.

Л. Кэррол

Кристаллы

Кристаллы белого фосфора образованы молекулами Р 4  . Такая молекула имеет вид тетраэдра.

Фосфорноватистая кислота

Н 3 РО 2.

Молекулы зеркальных изомеров молочной кислоты .

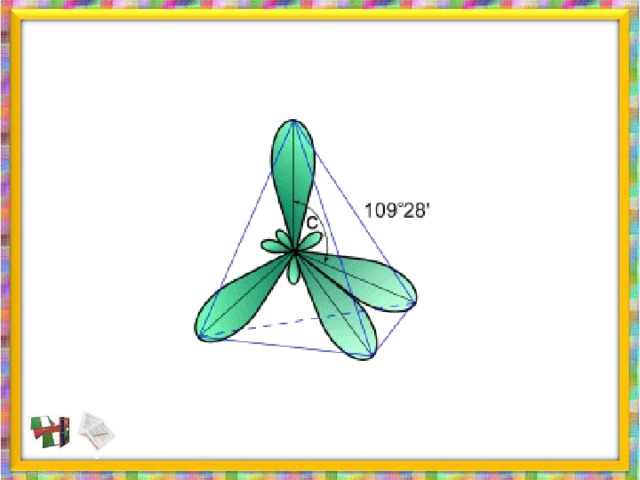
Строение молекулы

метана .

Строение решетки алмаза.

Кристаллы поваренной соли.

Вирус полиомиелита имеет форму додекаэдра.

Феодария

( Circjgjnia icosahtdra)

«Тайняя вечеря» С.Дали

ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»

Правильная форма алмаза.

Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка различным знаменитостям.

Интернет- источники:

Иллюстрации

http://www.techgate.ru/wallpicagen.php?image=6_423

http://dic.academic.ru/dic.nsf/enc_colier/6340/МНОГОГРАННИК

http://s53.radikal.ru/i140/0910/01/d6a003cbe3ba.jpg

http://denis-gorskin.narod.ru/algebra-2009/gipotez.html

http://900igr.net/fotografii/geometrija/Mnogogrannik-2/009-Pravilnye-mnogogranniki-i-priroda.html

http://900igr.net/fotografii/geometrija/Mnogogrannik-2/008-Salvador-Dali.html

http://900igr.net/fotografii/geometrija/Mnogogrannik-2/006-Kosmicheskij-kubok-Keplera.html

http://www.metodikinz.ru/goods/?page=.math.platon&dept=1

http://luarsoll.narod.ru/Biseropletenie.html

http://festival.1september.ru/articles/594729/

http://files.school-collection.edu.ru/dlrstore/ce2bd098-2ee2-9c4b-025f-2ce51c2f5fa5/7257_001.gif

http://www.referat-web.ru/content/referat/physics/img5717.jpg

http://school-sector.relarn.ru/nsm/chemistry/Rus/Data/Text/Ch3_2-11/img006.gif http://ido.tsu.ru/schools/chem/data/res/neorg/uchpos/text/img/g3_7_10.gif

http://www.krugosvet.ru/images/1011107_6739_003.gif

http://www.mnedrug.ru/index_1.php

http://znaniya-sila.narod.ru/people/004_00.htm http://znaniya-sila.narod.ru/people/004_00.htm

http://photo.peoples.ru/science/mathematics/louis_poinsot/poinsot_1.html

http://nl.wikipedia.org/wiki/Johannes_Kepler

http://www.sciencephoto.com/media/224346/enlarge

http://www.teor-meh.ru/bio/ik/koshi_ogyusten_lui.html

http://www.videoscan.ru/page/712