Занятие №1
Теорема Чевы.
Историческая справка.
Джованни Чева родился в 1647 году в Италии. Он окончил иезуитский колледж в Милане, после чего стал студентом Университета в Пизе, где позже и начал работу профессором математики.
С 1686 года Чева работал в Университете в Мантуе,
В 1678-м Чева опубликовал свою, ставшую знаменитой, теорему 'О взаимнопересекающихся прямых' о синтетической геометрии треугольника
Определение. Отрезки, соединяющие вершины треугольника с точками на противолежащих сторонах (или их продолжениях), называют чевианами, если они пересекаются в одной точке.
Возможны два варианта расположения чевиан. В одном варианте точка
пересечения – внутренняя, а концы чевиан лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного чевиана лежит
на стороне, а у двух других чевиан концы лежат на продолжениях сторон (смотри чертежи).
Медиана – отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
Биссектриса – луч с началом в вершине угла, делящий угол на два равных угла.
Высота – перпендикуляр, опущенный на сторону треугольника.
Теорема 3. (Прямая теорема Чевы) В произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты соответственно точки А1, В1, С1, такие, что прямые АА1, ВВ1, СС1 пересекаются в некоторой общей точке, тогда
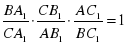 .
.
Теорема 4. (Обратная теорема Чевы). Если для выбранных на сторонах треугольника ABC или их продолжениях точек A1, В1 и C1 выполняется условие Чевы:
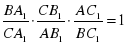 ,
,
то прямые AA1, BB1 и CC1 пересекаются в одной точке.
Следствие1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Следствие 2. Биссектрисы треугольника пересекаются в одной точке.
Следствие3. Высоты треугольника (или их продолжения) пересекаются в одной точке.
Следствие4. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Следствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке.
Решение задач.
№1. Докажите, что медианы треугольника пересекаются в одной точке.
Решение: Доказательство.
Так как точки А1, С1, В1 лежат на сторонах треугольника, достаточно доказать, что выполняется равенство :
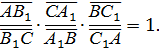
Так как ВВ1, СС1, АА1 медианы, то:
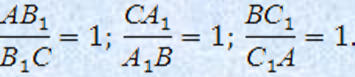
Тогда в силу теоремы Чевы прямые ВВ1, СС1, АА1 пересекаются в одной точке. Ч.т.д
№2. Докажите что высоты остроугольного треугольника пересекаются в одной точке.
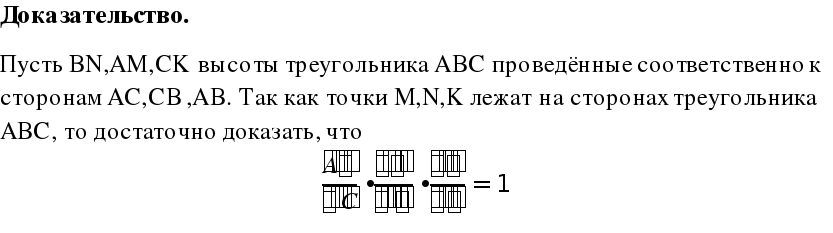
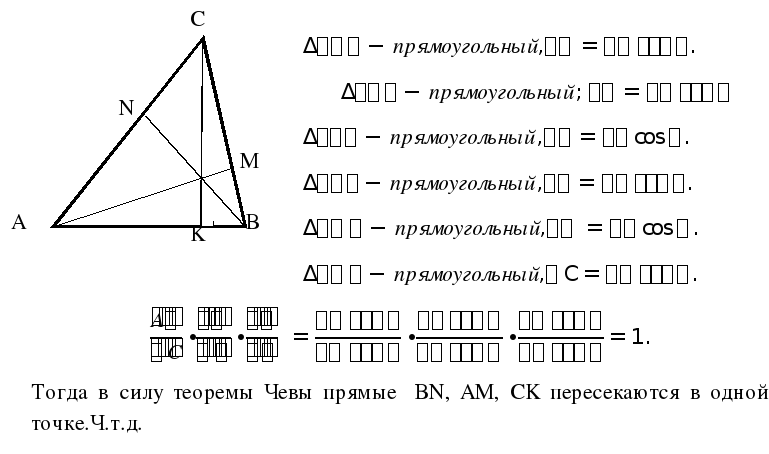
Для примера рассмотрим решение задачи С-4 из тренировочной работы № 10 (Сборник «ЕГЭ, 2014. Математика. 30 вариантов типовых тестовых заданий и 800 заданий части 2 (С)/ под редакцией А.Л.Семёнова, И.В.Ященко.- М.: Издательство «Экзамен», 2014.-215»).
Задача. Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника АВС, причём АВ1:В1С=АС1:С1В. Прямые ВВ1 и СС1 пересекаются в точке О. (рис 2)
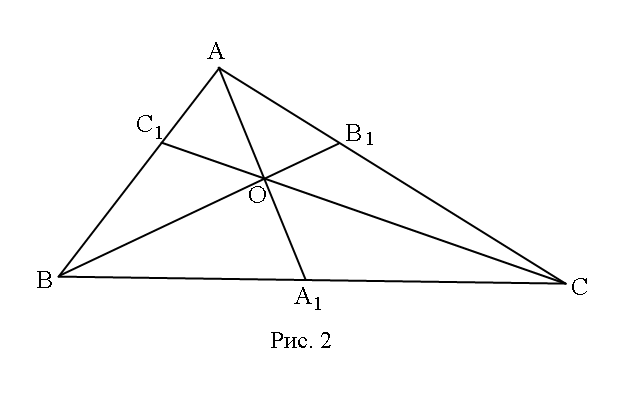
а) Докажите, что прямая АО делит пополам сторону ВС.
б) Найдите отношение площади четырёхугольника АВ1ОС1 к площади треугольника АВС, если известно, что АВ1:В1С=АС1:С1В=1:2
Доказательство:
Значительно упрощает доказательство применение теоремы Чевы. Итак, если все три прямые пересекаются в одной точке, то по теореме выполняется равенство:
 .
.
Так как по условию  , то получим
, то получим  . Откуда
. Откуда  или
или  , что и требовалось доказать.
, что и требовалось доказать.
Для того, чтобы найти  при условии
при условии  будем рассуждать следующим образом (рис 3).
будем рассуждать следующим образом (рис 3).
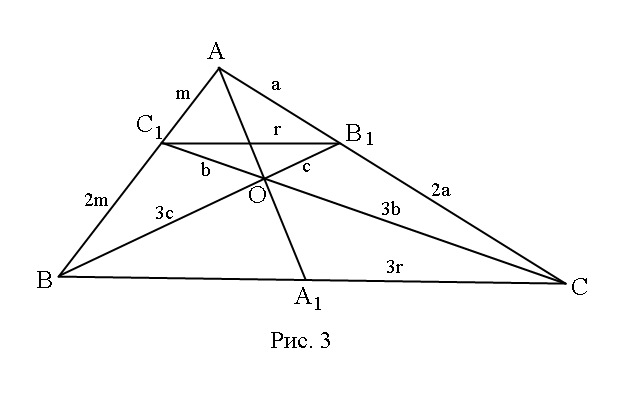
Пусть  ,
,  ,
,  ,
,  .
.  ( по второму признаку). Следовательно,
( по второму признаку). Следовательно,  .
.
 ( по двум углам).
( по двум углам).  .
.
 ( как площади треугольников, имеющих общий угол). Значит,
( как площади треугольников, имеющих общий угол). Значит, 

 ( как площади треугольников, имеющих общую высоту). Значит,
( как площади треугольников, имеющих общую высоту). Значит,  .
.
 . Тогда
. Тогда  .
.







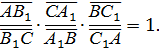



 .
.



















