Конспект урока математики
«Площадь криволинейной трапеции и интеграл», 11 класс
Цели:
Предметные -получить представление о понятии интеграла, криволинейной трапеции, площади криволинейной трапеции
Метапредметные - уметь самостоятельно принимать решения, проводить анализ своей деятельности; проявлять инициативу и самостоятельность в обучении.
Личностные - работать над критичностью мышления, быть инициативным, находчивым ;развитие самостоятельности, доброжелательного отношения, эмоциональной отзывчивости.
Задачи:
Образовательные:
сформировать понятие интеграла;
формирование навыков вычисления определенного интеграла;
формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.
Развивающие:
развитие познавательного интереса учащихся, развивать математическую речь, умения наблюдать, сравнивать, делать выводы;
Воспитательные:
активизировать интерес к получению новых знаний, формирование точности и аккуратности при вычислении интеграла и выполнении чертежей.
Ход урока.
1) Разминка Для разминки предлагаю выполнить следующие задания
Найдите площадь фигуры: параллелограмм, треугольник, трапеция

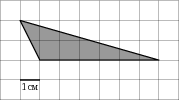
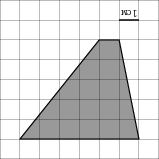

Задачу нахождения площади фигур люди ставили перед собой с древних времен, это связано с сугубо практическим характером.
Вычисление площадей простейших фигур не составляет труда: надо в известные формулы подставить исходные данные. А как быть, если фигура имеет сложные формы?
Создание проблемной ситуации
Н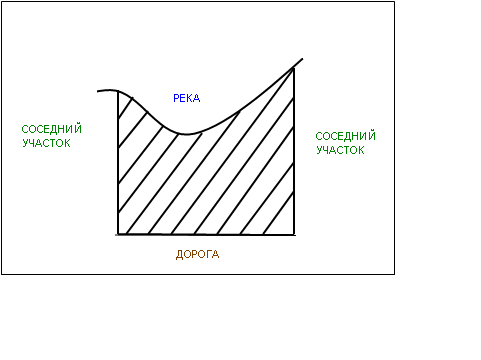 алоговая инспекция прислала вам уведомление о том, что сумма земельного налога за год составляет 5 000 руб. Сумма налога зависит от площади и рыночной стоимости земельного участка. Вы посчитали, что налог начислен не правильно. Что вам нужно сделать, чтобы рассчитать налог?
алоговая инспекция прислала вам уведомление о том, что сумма земельного налога за год составляет 5 000 руб. Сумма налога зависит от площади и рыночной стоимости земельного участка. Вы посчитали, что налог начислен не правильно. Что вам нужно сделать, чтобы рассчитать налог?
Какая геометрическая фигура представлена на чертеже?(похожа на трапецию, но одна сторона кривая линия)
Вспомните, о чем мы говорили на прошлом уроке?(С каким понятием работаем)
Как вы думаете, можем ли мы применить первообразную для вычисления площади криволинейной трапеции?
А теперь давайте вместе постараемся сформулировать тему сегодняшнего урока?
Скажите, пожалуйста, чтобы вы хотели узнать на уроке по этой теме?
А чему хотите научиться?
Сегодня вы узнаете, что представляет собой такая фигура как криволинейная трапеция, а также будете учиться вычислять площадь криволинейной трапеции.
2) Подготовка к восприятию нового материала (Повторение ранее изученного материала)
Но сначала нам необходимо проверить умения находить первообразные элементарных функций.
В рабочих листах
Задание №1. Восстановить таблицу первообразных(взаимопроверка, по цепочке)

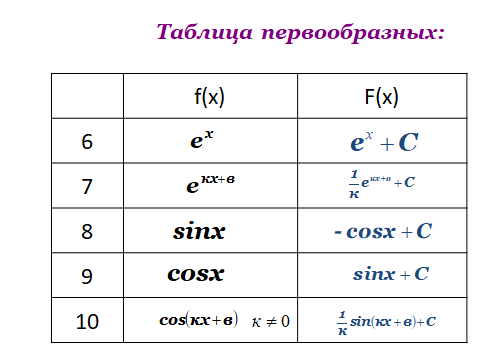
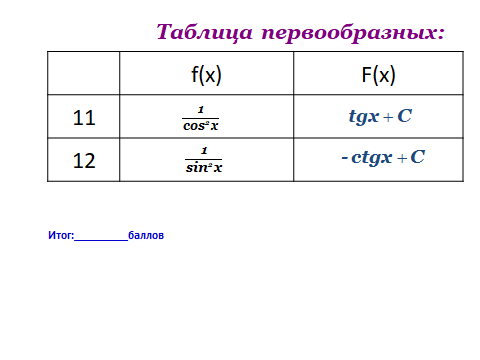
Задание №2. Поставить в соответствие функцию и ее первообразную(самопроверка)

3) Изучение нового материала
Переходим к теме нашего занятия «Площадь криволинейной трапеции и интеграл».
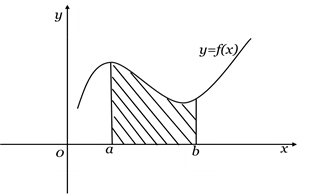
Рассмотрим фигуру, изображенную на рисунке.
(дописать определение в рабочем листе)
Фигура, ограниченная снизу отрезком [a;b] оси Ох , сверху графиком непрерывной и неотрицательной функции y=f(x), а с боков отрезками прямых x=a и x=b , называется криволинейной трапецией.
Отрезок [a; b] называют основанием криволинейной трапеции.
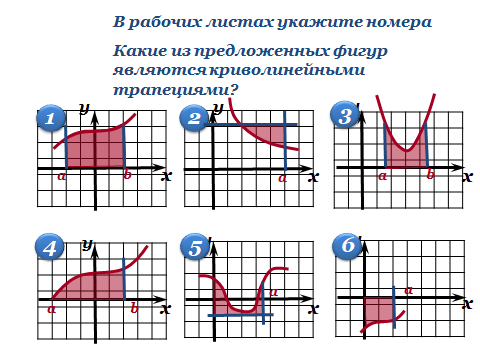
Устно. Определите, на каких рисунках изображены криволинейные трапеции. Ответ обоснуйте.
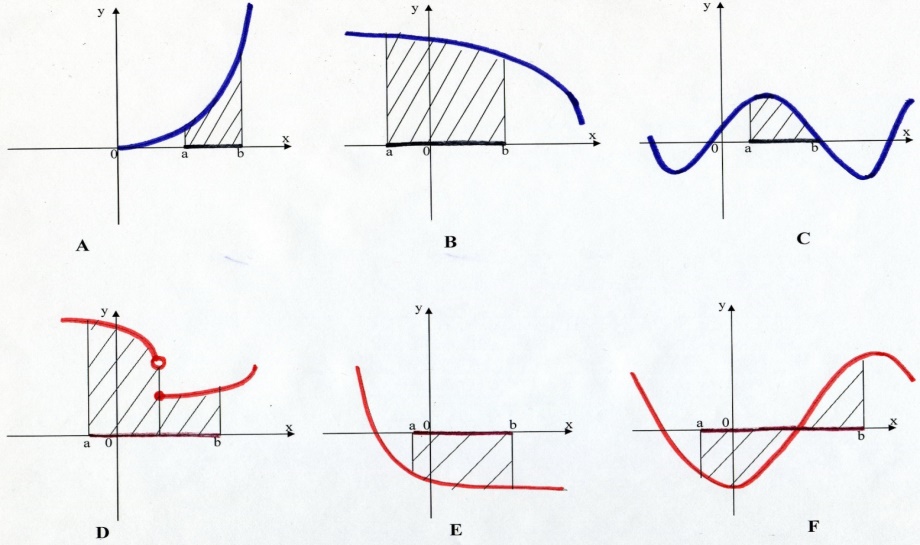
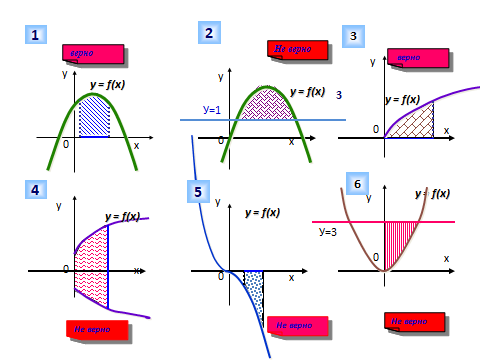
Задание №3. Указать номера рисунков, где изображены криволинейные трапеции
Для вычисления площади криволинейной трапеции применяется формула:
S=F(b) – F(a)
Р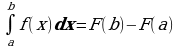 азность F(b) – F(a) называется интегралом от функции f(х) на отрезке [а;b] и обозначают:
азность F(b) – F(a) называется интегралом от функции f(х) на отрезке [а;b] и обозначают:
формула Ньютона–Лейбница.
Объединяя эти формулы

Решим задачу на вычисление площади криволинейной трапеции:
Найти площадь криволинейной трапеции, ограниченной графиком функции y =  , прямыми x = 1, x = 3 и осью OX.
, прямыми x = 1, x = 3 и осью OX.
(Решение задачи объясняет учитель)
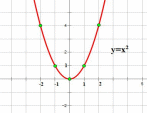 Сначала изобразим криволинейную трапецию, заданную указанным образом.
Сначала изобразим криволинейную трапецию, заданную указанным образом.
-построим график квадратичной функции;
-проведем прямые x = 1, x = 3 .
Затем, используя формулу Ньютона-Лейбница , найдем
S = 1 ∫3  =
= 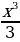 │
│ =
= 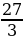 -
- =
= 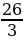 =
=  кв.ед.
кв.ед.
Алгоритм нахождения площади криволинейной трапеции
1.Построить график заданной непрерывной функции
2.Отметить отрезок  , прямые х=a и x=b, выделить криволинейную трапецию.
, прямые х=a и x=b, выделить криволинейную трапецию.
3.Используя формулу Ньютона-Лейбница, найти площадь криволинейной трапеции
4) Закрепление изученного материала.
(Совместное решение)
1) Изобразить криволинейную трапецию, ограниченную графиком функции
y = (x - 1)2 , осью OX прямой x = 2 . Найти площадь трапеции.
2) Найти площадь криволинейной трапеции, ограниченной графиком функции y=2sinx , прямыми х=0 и х=π и осью OX.
Вычислите площадь фигуры, изображенной на рисунке.

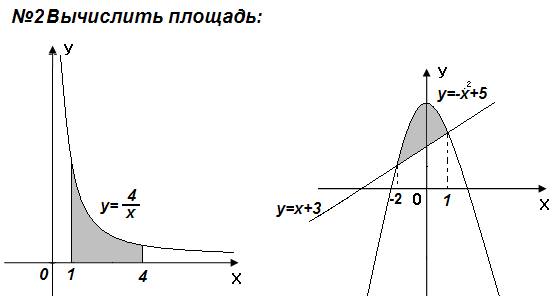
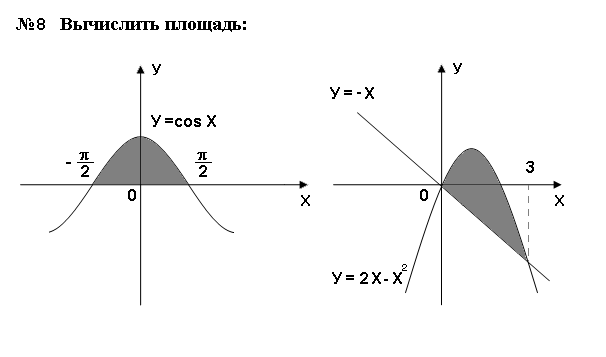
Самостоятельно:
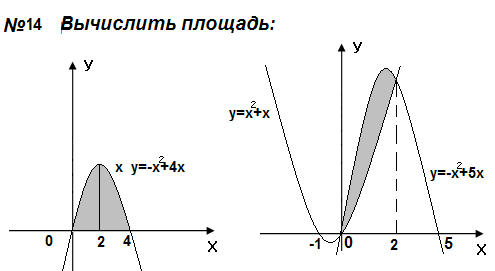

5) Домашнее задание.
Прочитать параграф 56 , разобрать, выучить формулы
№1000(1,3,5)
№1505(1) точки экстремума
6) Рефлексия «Акрослово»
И
Н
Т
Е
Г
Р
А
Л
7) Подведение итогов урока.
Что сегодня изучили на уроке?
Что называют криволинейной трапецией?
Как вычисляется площадь криволинейной трапеции?
Сформулируйте основные шаги вычисления площади криволинейной трапеции.
Выставить оценки.











 алоговая инспекция прислала вам уведомление о том, что сумма земельного налога за год составляет 5 000 руб. Сумма налога зависит от площади и рыночной стоимости земельного участка. Вы посчитали, что налог начислен не правильно. Что вам нужно сделать, чтобы рассчитать налог?
алоговая инспекция прислала вам уведомление о том, что сумма земельного налога за год составляет 5 000 руб. Сумма налога зависит от площади и рыночной стоимости земельного участка. Вы посчитали, что налог начислен не правильно. Что вам нужно сделать, чтобы рассчитать налог?







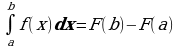 азность F(b) – F(a) называется интегралом от функции f(х) на отрезке [а;b] и обозначают:
азность F(b) – F(a) называется интегралом от функции f(х) на отрезке [а;b] и обозначают: 
 , прямыми x = 1, x = 3 и осью OX.
, прямыми x = 1, x = 3 и осью OX. Сначала изобразим криволинейную трапецию, заданную указанным образом.
Сначала изобразим криволинейную трапецию, заданную указанным образом. =
= 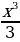 │
│ =
= 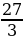 -
- =
= 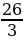 =
=  кв.ед.
кв.ед. , прямые х=a и x=b, выделить криволинейную трапецию.
, прямые х=a и x=b, выделить криволинейную трапецию.














