Тема урока: «Площадь криволинейной трапеции. Интеграл. Формула Ньютона-Лейбница».
Тип урока: Изучение нового материала.
Продолжительность занятия: 90 минут.
Цели урока: ввести понятие площади криволинейной трапеции: интеграла и его вычисление по формуле Ньютона-Лейбница, используя знания о первообразной и правила ее вычисления; проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; закрепить изученное в ходе выполнения упражнений.
Задачи урока:
Образовательные:
Сформировать понятие площади криволинейной трапеции;
сформировать понятие интеграла;
формирование навыков вычисления определенного интеграла;
формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.
Развивающие:
развитие познавательного интереса учащихся, развивать математическую речь, умения наблюдать, сравнивать, делать выводы;
Воспитательные:
активизировать интерес к получению новых знаний, формирование точности и аккуратности при вычислении интеграла и выполнении чертежей.
Ход урока
Организационный опрос.
Постановка цели.
Самостоятельная работа.
Объяснение нового материала.
Закрепление.
Итоги. Домашнее задание.
Тема: Площадь криволинейной трапеции. Интеграл. Формула Ньютона-Лейбница.
III. Самостоятельная работа. (Приложение 1).
1 вариант
| Дана функция | 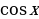
| 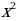
| 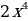
| 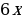
| 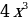
| 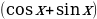
|
| Найдите первообразную от исходной функции | 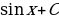
| 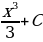
| 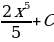
| 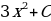
| 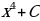
| 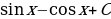
|
2 вариант
| Дана функция | 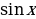
| 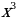
| 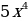
| 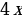
| 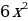
| 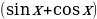
|
| Найдите первообразную от исходной функции | 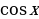
| 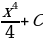
| 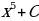
| 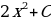
| 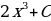
| 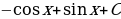
|
IV. Объяснение нового материала.
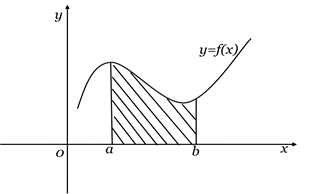 Опр.: Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке
Опр.: Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке  функции
функции  , осью
, осью  и прямыми
и прямыми 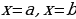 .
.
Рис.1
Теорема: Пусть 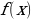 – непрерывная и неотрицательная функция на отрезке
– непрерывная и неотрицательная функция на отрезке 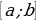 функция, а
функция, а 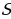 – площадь соответствующей криволинейной трапеции (рис.1). Если
– площадь соответствующей криволинейной трапеции (рис.1). Если 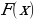 – есть первообразная для
– есть первообразная для 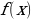 на интервале, содержащем отрезок
на интервале, содержащем отрезок 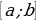 , то
, то
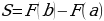
Пример: Вычислить площадь фигуры, ограниченной линиями:
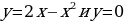 ;
;
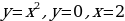 .
.
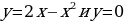
Графиком криволинейной трапеции является парабола, ветви которой направлены вверх. Найдем вершину (m;n) этой параболы.
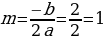
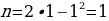
(1;1) – вершина параболы.
Найдем точки пересечения 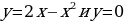
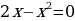
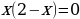
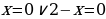
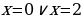
Значит, 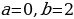
Найдем первообразную для функции 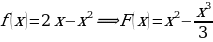
Найдем площадь криволинейной трапеции:
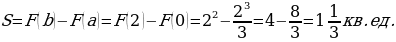
Ответ: 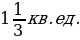
Второе задание самостоятельно.
Опр.: Интегралом от 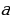 до
до 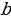 функции
функции 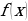 называется приращение первообразной
называется приращение первообразной 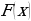 этой функции, т.е.
этой функции, т.е. 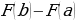 .
.
Интеграл от от 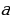 до
до 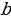 функции
функции 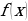 обозначается т.о.
обозначается т.о. 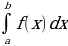 , где
, где 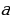 – нижний,
– нижний, 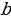 – верхний предел интегрирования,
– верхний предел интегрирования, 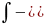 знак интегрирования,
знак интегрирования, 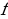 – подынтегральная функция,
– подынтегральная функция, 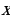 – переменная интегрирования.
– переменная интегрирования.
По определению интеграла: если 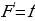 , то
, то
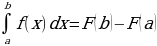 – формула Ньютона – Лейбница
– формула Ньютона – Лейбница
Для удобства 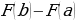 обозначается
обозначается 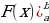
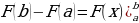
Формула для вычисления площади криволинейной трапеции:
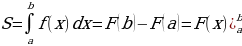
V. Закрепление материала.
1. Вычислить интеграл.
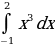 ;
;
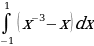 ;
;
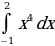 ;
;
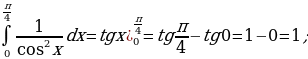
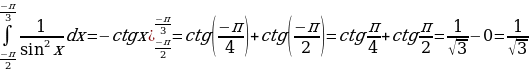 ;
;
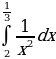 ;
;
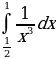 .
.
2. Вычислить площадь фигуры, ограниченной линиями:
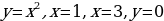 ;
;
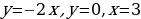 ;
;
Итоги. Домашнее задание:
Вычислить интеграл:
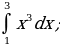
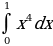 ;
;
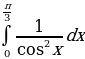 ;
;
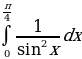 ;
;
Вычислить площадь фигуры, ограниченной линиями: 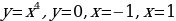 .
.
Приложение 1
1 вариант
| Дана функция | 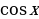
| 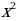
| 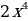
| 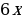
| 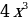
| 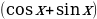
|
| Найдите первообразную от исходной функции |
|
|
|
|
|
|
2 вариант
| Дана функция | 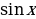
| 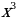
| 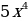
| 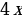
| 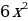
| 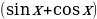
|
| Найдите первообразную от исходной функции |
|
|
|
|
|
|
1 вариант
| Дана функция | 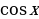
| 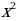
| 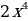
| 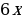
| 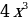
| 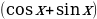
|
| Найдите первообразную от исходной функции |
|
|
|
|
|
|
2 вариант
| Дана функция | 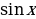
| 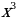
| 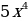
| 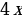
| 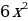
| 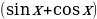
|
| Найдите первообразную от исходной функции |
|
|
|
|
|
|
1 вариант
| Дана функция | 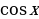
| 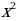
| 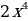
| 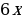
| 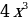
| 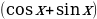
|
| Найдите первообразную от исходной функции |
|
|
|
|
|
|
2 вариант
| Дана функция | 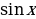
| 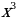
| 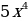
| 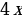
| 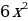
| 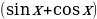
|
| Найдите первообразную от исходной функции |
|
|
|
|
|
|







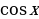
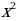
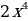
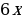
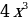
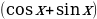
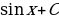
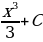
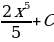
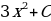
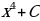
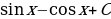
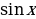
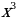
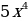
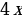
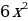
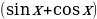
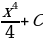
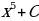
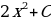
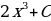
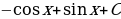
 Опр.: Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке
Опр.: Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке 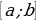 функции
функции 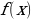 , осью
, осью 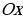 и прямыми
и прямыми 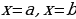 .
.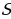 – площадь соответствующей криволинейной трапеции (рис.1). Если
– площадь соответствующей криволинейной трапеции (рис.1). Если 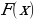 – есть первообразная для
– есть первообразная для 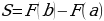
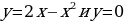 ;
;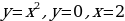 .
.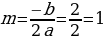
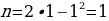
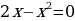
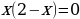
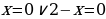
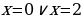
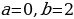
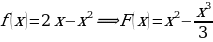
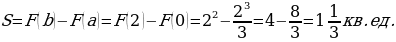
 до
до  функции
функции 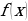 называется приращение первообразной
называется приращение первообразной 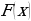 этой функции, т.е.
этой функции, т.е. 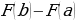 .
.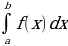 , где
, где 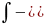 знак интегрирования,
знак интегрирования, 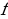 – подынтегральная функция,
– подынтегральная функция, 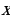 – переменная интегрирования.
– переменная интегрирования.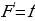 , то
, то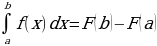 – формула Ньютона – Лейбница
– формула Ньютона – Лейбница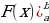
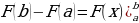
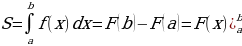
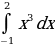 ;
;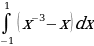 ;
;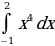 ;
;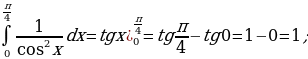
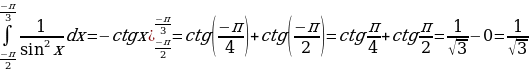 ;
;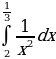 ;
;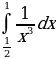 .
.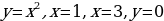 ;
;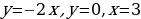 ;
;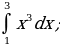
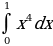 ;
;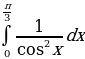 ;
;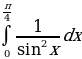 ;
;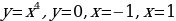 .
.









