Урок по теме: Средняя линия треугольника

МБОУ Жирновская СОШ, Тацинский район, Ростовская область

Учитель математики: Волкова Татьяна Валентиновна.

Урок геометрии по теме: Средняя линия треугольника.

8 класс

Образовательные цели:

• Познакомить учащихся со средней линией треугольника и её свойством;

• Сформулировать на основе имеющихся знаний доказательство свойства средней линии треугольника;

• Формировать умение решать задачи, на применение свойства средней линии треугольника.

Развивающие цели:

• Развивать графические навыки учащихся при построении средних линий треугольника, развивать навыки исследовательской деятельности;

• Формировать и развивать умения анализировать свою деятельность при решении задач и доказательстве теоремы;

• Формировать умения извлекать необходимую информацию и использовать ее для поиска ответа на вопрос, переносить знания в новые ситуации.

Воспитательные цели:

• Формировать умения слушать мнения других, отстаивать свою точку зрения;

• Развивать познавательный интерес к предмету.

Ход урока:

1. Организационный момент. Тема, цели урока.

Слайд 1.

Вступительное слово учителя.

Слайд 2.

«Любопытный отыскивает редкости только затем, чтобы им удивляться, любознательный же затем, чтобы узнать их и перестать удивляться» Р. Декарт.

Я хочу, что бы сегодня на уроке вы были не только любопытными, но и любознательными.

Геометрия очень интересная наука и довольно глубоко изучена, но для нас всё же в ней ещё много тайн. И раскрытие некоторых из них нас сегодня ждут на уроке.

1. Актуализация знаний. Подготовка к изучению нового материала.

Слайд 3.

Мы сейчас вспомним, что мы знаем о подобных треугольниках: (4 менее подготовленных

-Какие треугольники мы называем подобными? учащихся работают над

тестами-карточками

самостоятельно)

-Какие пары треугольников подобны? Почему? (Один ученик на ИД соединяет

стрелками пары подобных Δ)

(Ученики отвечают на вопросы с

необходимой аргументацией).

- Сформулируйте признаки подобия треугольников.

1. Изучение нового материала.

Слайд 4.

Всегда интересно открывать, что – то новое. Особенно если это открытие ты сделал сам. Проведём исследовательскую работу, которая поможет нам сделать «научное открытие». Работать будем на модулях, на которых у вас готовые чертежи. Следуйте указаниям чётко и быстро, и тогда у вас обязательно всё получится. Работаем в группах. (1 группа работает с остроугольным Δ, 2 группа с тупоугольным Δ, 3 группа с прямоугольным Δ.)

-Измерьте основание АВ, результат запишите. (Один ученик выполняет на ИД,

-Измерьте боковые стороны АС и ВС, результат запишите. остальные в модулях)

-В середине АС и ВС поставьте соответственно точки М и К.

-Проведите отрезок МК. (вводится определение средней линии).

Определение: отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

- Измерьте длины отрезков МК и АВ.

-Сравните длину отрезка МК и длину стороны АВ. Ответьте на вопрос: во сколько раз длина отрезка МК меньше длины стороны АВ.

-Сформулируйте гипотезу. (Ученики исследуют, анализируют,

сопоставляют, каждая группа

высказывает свои гипотезы)

Вывод (делает учитель, анализируя гипотезы учеников): проведённое исследование показывает, каков бы ни был треугольник его средняя линия всегда в два раза меньше одной из его сторон. Я поздравляю, сейчас каждый открыл для себя новую теорему, которую мы сейчас докажем.

Слайд 5.

Теорема:

Средняя линия треугольника параллельна его стороне и равна её половине.

Доказательство:

Пусть MN– средняя линия ∆ABC. Докажем, что MNǁAC и MN=AC:2.

∆ABC∾∆MBN по второму признаку (объясните): (Ученики объясняют с

необходимой аргументацией)

(∠B – общий, BM/BA= BN/BC=1/2 )(что следует из подобия Δ?) (Ученики отвечают на

∠1=∠2 и MN/AC=1/2. (что из этого может следовать?) поставленные вопросы)

Из того, что ∠1=∠2 следует, что MNǁAC, а из MN/AC=1/2 следует, что MN=AC/2.

(Учитель ещё раз сам полностью доказывает теорему.)

1. Первичное осмысление и закрепление нового материала.

Слайд 6.

Решение задач на готовых чертежах: По данным рисунков установить, являются ли отрезки средними линиями?

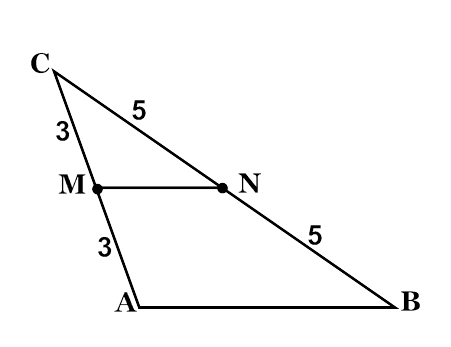
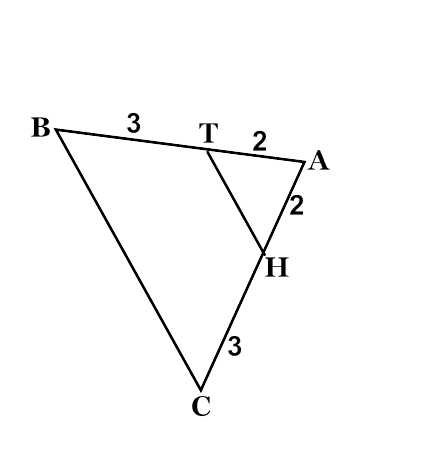
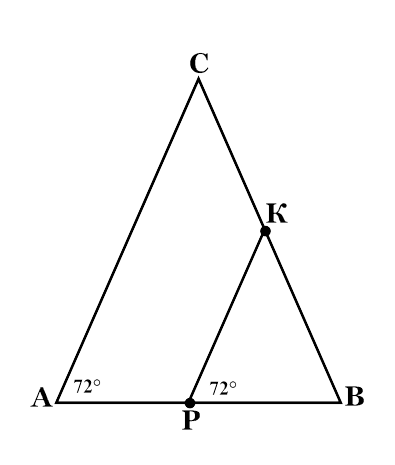(Ученики отвечают на вопросы

с необходимой аргументацией).

Построение средней линии треугольника.

Слайд 7.

Построение средней линии треугольника (1-й способ).

(Попробуйте сформулировать алгоритм построения (Ученики предлагают свои варианты)

средней линии треугольника самостоятельно,

следуя из определения).

Учитель обобщает ответы учеников и предлагает

выполнить построение по алгоритму.

• Начертите произвольный треугольник ABC. (Ученики строят среднюю линию,

• Отметьте середины сторон AB и BC. по предложенному алгоритму

и обозначьте соответственно N и М . в модулях. Один ученик выполняет

• Соедините N и М отрезком. построение на доске. Учитель

NM - средняя линия треугольника ABC демонстрирует на ИД)

Слайд 8.

Построение средней линии треугольника (2-й способ).

Учитель предлагает другой способ построения средней линии.

• Начертите произвольный треугольник ABC. (Ученики строят среднюю линию,

• С помощью линейки разделите сторону АВ. по предложенному алгоритму

на две равные части и середину обозначьте N. в модулях. Один ученик выполняет

• Через точку N проведите прямую, параллельную построение на доске. Учитель

стороне AC. демонстрирует на ИД)

• Обозначьте точку пересечения прямой со стороной ВС

через М.

• Измерьте длины отрезков BM и MC и сделайте вывод. (Ученики анализируют и делают NM - средняя линия треугольника ABC. вывод)

5.Физ.минутка.

Учитель говорит стихотворение и показывает движения. (Ученики слушают и повторяют

Быстро встали, улыбнулись, за учителем несложные движения)

Выше-выше подтянулись.

Ну-ка плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Вздохнули дружно.

Нам урок продолжить нужно.

Подравнялись, тихо сели

И на доску посмотрели.

6. Закрепление изученного материала.

Работа с учебником.

Слайд 9.

Задача № 564

Дано: ∆ABC,

AB=8 см, BC=5 см, CA=7 см, AM=MB, BN=NC, CP=PA

Найти: P_∆MNP

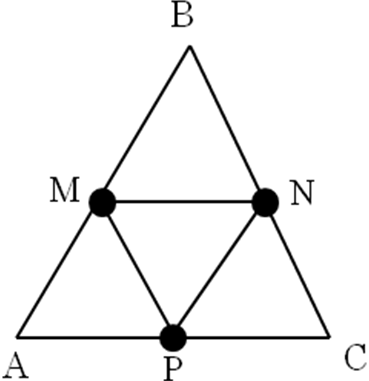(Один ученик решает у доски с

аргументацией. Остальные решают

задачу на месте в тетрадях,

сверяются с тем, что на доске,

задают вопросы учителю. Ученики,

решившие значительно раньше

задачу, показывают решение

учителю на оценку.)

Подсказки и вопросы:

- Обратите внимание на стороны нового треугольника. Чем они являются для ∆ABC?

- В каком соотношении находятся ∆ABC и ∆MNP?

Решение

AM=MB, BN=NC, CP=PA то MN, NP, PM – средние линии ∆ABC. P_∆MNP=MN+NP+PM=AC/2+AB/2+BC/2=(7+8+5)/2=10 (см).

Ответ. P_∆MNP =10 см.

Слайд 10.

Задача № 567

Д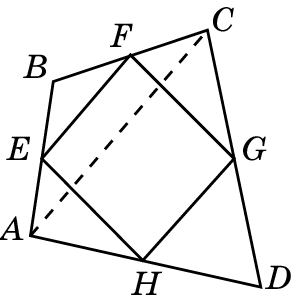 ано: ABCD – четырехугольник,

E, F, G, H – середины его сторон. (Ученики решают задачу устно,

Доказать: EFGH – параллелограмм. под руководством учителя)

Подсказки и вопросы:

- Обратите внимание на диагональ АС. Чем она является в ΔABC и ΔACD.

Решение

Пусть ABCD – четырехугольник. E, F, G, H – середины его сторон. Проведем диагональ AC. EF – средняя линия ΔABC и, следовательно, параллельна AC и равна ее половине. Аналогично, HG – средняя линия Δ ACD и, следовательно, параллельна AC и равна ее половине. Таким образом, стороны EF и HG четырехугольника EFGH равны и параллельны. Значит, этот четырехугольник – параллелограмм.

С лайд 11.

Практическое применение:

Знания о средней линии треугольника так же можно использовать в сельском хозяйстве.

К примеру, найти длину поля.

Задача:

Найти длину поля, если в ней оказалось сто «шагов» полевого

циркуля при условии, что DE = 1м, АD=DB, CE=BE.

(Ученики решают задачу устно)

Решение

АD=DB, CE=BE, то DE – средняя линия ∆ABC, DE=1/2AC значит AC=2DE = 2·1= 2м.

2·100= 200м.

Ответ. 200м

Слайд 12.

Из подобных треугольников, которые получены путём разрезания по средним линиям, можно составить новую геометрическую фигуру, части которой подобны целому треугольнику. Учёные назвали такие фигуры автоподобными. (автоподобная фигура - фрактал ).

До начала 20 века автоподобные фигуры совершенно не изучались. Считалось, что они не являются полноправными математическими объектами, и поэтому их изучение отбрасывалось. Но идеи изучения автоподобных фигур были развиты Б. Мандельбротом. Он в 1975 году ввёл слово «фрактал» (от которого позднее произошли английские термины – дробь, дробный).

Слайд 13.

"Звезда Коха"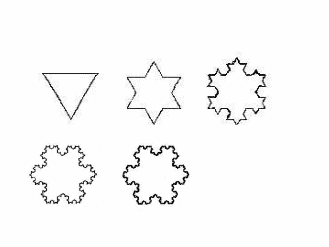

Слайд 14.

Аналогичное свойство самоподобия обнаруживают многие объекты в природе, стоит лишь повнимательнее к ним присмотреться.

Примером автоподобной фигуры является золотая спираль, геометрическим свойством этой спирали является то, что каждый следующий виток подобен предыдущему. В форме золотой спирали закручиваются раковины многих моллюсков, в виде этой спирали плетут свою паутину пауки и даже галактика солнечной системы закручивается по золотой спирали.

Слайд 15.

7.Итог урока.

• Какой отрезок называют средней линией треугольника?

• Сколько средних линий может быть в треугольнике? (Ученики отвечают на Какими способами можно построить среднюю линию Δ? поставленные вопросы)

• Каким свойством обладает средняя линия треугольника?

Слайд 16.

8.Рефлексия. (Ученики отвечают на

Что вы узнали нового? вопросы с необходимой

Чему научились? аргументацией)

Что показалось особенно трудным?

Понравился ли урок? (Высказывают свое отношение к уроку

с помощью поднятых сигнальных карточек.

Зеленая – урок понравился, много нового узнал.

Желтая – не совсем понял тему, но что-то

новое узнал.

Красная – урок не понравился.)

Слайд 17.

9.Д\З. №565,566 выучить определение средней линии треугольника и доказательство теоремы о средней линии треугольника и найти другие способы доказательства в дополнительной литературе. (Записывают, слушают, задают вопросы)

Сегодня все хорошо работали, были и любопытными и любознательными, открыли для себя новую теорему, закрепили её при решении задач, и поэтому у нас много зеленых и желтых карточек. И за урок вы получаете оценки… .

Слайд 18.

Спасибо за урок!

Список литературы

• Устные упражнения по геометрии для 7-11 классов. Кн. для учителя /И.М. Смирнова, В.А. Смирнов – М.: Просвещение, 2005

• Упражнения по планиметрии на готовых чертежах: Пособие для учителя. Авторы: С.М. Саврасова, Г.А. Ястребинецкий – М.: Просвещение, 1987

• Задачи по геометрии. Пособие для учащихся 7 -11 кл. общеобразовательных учреждений /Б.Г.Зив, В.М. Мейлер, А.Г. Баханский – 3-е изд. – М.: Просвещение, 2008

• Геометрия, 7-9: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И.Юдина – 15 изд. – М.: Просвещение, 2010

• Геометрия 7-9: учебник для 7-9 классов общеобразовательных учреждений. Под ред. А.Я. Цукаря. / В.Н. Руденко, Г.А. Бахурин - 2-е изд. – М.: Просвещение, 1994

Сайты:

Мой университет – www.moi-mummi.ru

http://festival.1september.ru/articles/527602/